二叉树1:深入理解数据结构第一弹——二叉树(1)——堆-CSDN博客
二叉树2:深入理解数据结构第三弹——二叉树(3)——二叉树的基本结构与操作-CSDN博客
二叉树3:深入理解数据结构第三弹——二叉树(3)——二叉树的基本结构与操作-CSDN博客
前言:
在之前我们用C语言实现数据结构时,已经对二叉树进行了系统的学习,但还是有一些内容并没有涉及到,比如今天要讲的二叉搜索树,因为二叉搜索树在C++中有现成的模板库——set和map,并且实现起来较为麻烦,所以我们放到这里来讲,对前面二叉树部分有所遗忘的同学可以在我的主页搜一下之前的文章看一下
目录
一、二叉搜索树的概念
二、二叉搜索树的基本操作
1. 插入节点
2. 查找节点
3. 删除节点
三、二叉搜索树的实现
四、二叉搜索树的应用
五、总结
一、二叉搜索树的概念
二叉搜索树又称二叉排序树,它是一种具有特殊性质的二叉树,它具有以下特点:
1. 有序性:对于树中的每个节点,其左子树中的所有节点的值都小于该节点的值,而其右子树中的所有节点的值都大于该节点的值。
2. 唯一性:树中的每个节点的值都是唯一的,不存在重复的值。
3. 递归性:它的子树也都是二叉树
上面这三种性质,最不好理解的应该是有序性,下面我们通过两个例子来展现这三种性质:
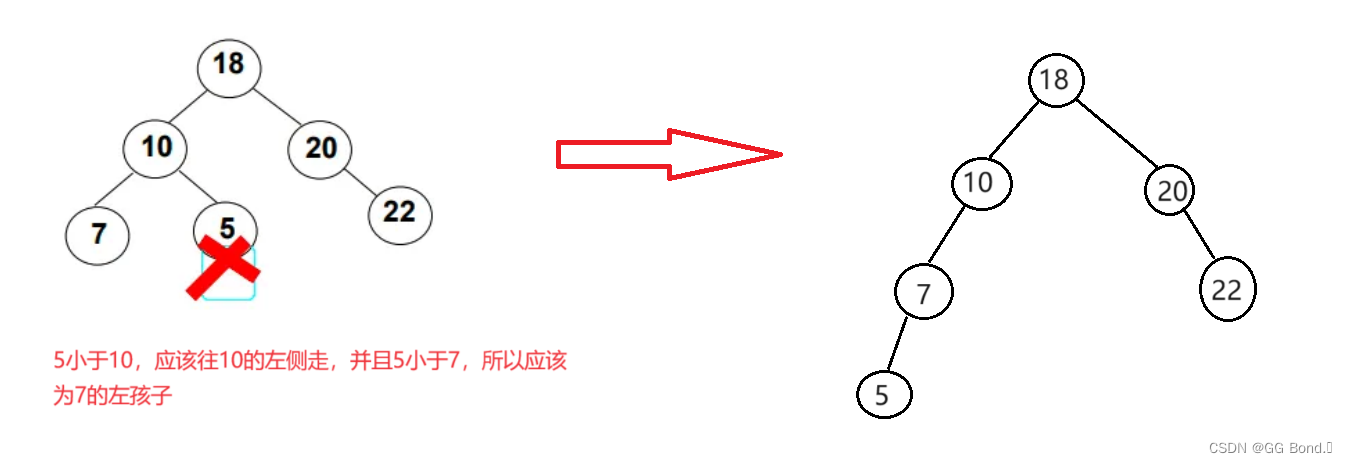
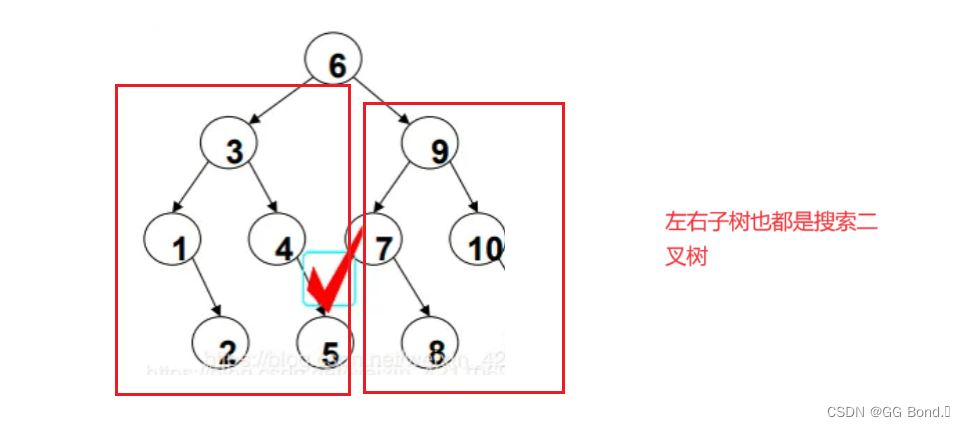
二、二叉搜索树的基本操作
1. 插入节点
插入节点的过程如下:
- 从根节点开始,比较要插入的值与当前节点的值。
- 如果要插入的值小于当前节点的值,则移动到左子节点;如果要插入的值大于当前节点的值,则移动到右子节点。
- 重复上述过程,直到找到一个空位置,然后在该位置插入新节点。
2. 查找节点
查找节点的过程如下:
- 从根节点开始,比较要查找的值与当前节点的值。
- 如果要查找的值等于当前节点的值,则返回该节点。
- 如果要查找的值小于当前节点的值,则移动到左子节点;如果要查找的值大于当前节点的值,则移动到右子节点。
- 重复上述过程,直到找到目标节点或遍历到空节点。
3. 删除节点
删除节点的过程相对复杂,需要考虑以下几种情况:
- 删除叶子节点:直接删除该节点。
- 删除只有一个子节点的节点:将其子节点替换到该节点的位置。
- 删除有两个子节点的节点:找到该节点右子树中的最小节点(或左子树中的最大节点),将其值替换到该节点的位置,然后删除该最小节点。
三、二叉搜索树的实现
template<class T>
struct BSTNode
{
BSTNode(const T& data = T())
: _pLeft(nullptr) , _pRight(nullptr), _data(data)
{}
BSTNode<T>* _pLeft;
BSTNode<T>* _pRight;
T _data;
};
template<class T>
class BSTree
{
typedef BSTNode<T> Node;
typedef Node* PNode;
public:
BSTree(): _pRoot(nullptr)
{}
// 自己实现,与二叉树的销毁类似
~BSTree();
// 根据二叉搜索树的性质查找:找到值为data的节点在二叉搜索树中的位置
PNode Find(const T& data);
bool Insert(const T& data)
{
// 如果树为空,直接插入
if (nullptr == _pRoot)
{
_pRoot = new Node(data);
return true;
}
// 按照二叉搜索树的性质查找data在树中的插入位置
PNode pCur = _pRoot;
// 记录pCur的双亲,因为新元素最终插入在pCur双亲左右孩子的位置
PNode pParent = nullptr;
while (pCur)
{
pParent = pCur;
if (data < pCur->_data)
比特就业课
pCur = pCur->_pLeft;
else if (data > pCur->_data)
pCur = pCur->_pRight; // 元素已经在树中存在
else
return false;
}
// 插入元素
pCur = new Node(data);
if (data < pParent->_data)
pParent->_pLeft = pCur;
else
pParent->_pRight = pCur;
return true;
}
bool Erase(const T& data)
{
// 如果树为空,删除失败
if (nullptr == _pRoot)
return false;
// 查找在data在树中的位置
PNode pCur = _pRoot;
PNode pParent = nullptr;
while (pCur)
{
if (data == pCur->_data)
break;
else if (data < pCur->_data)
{
pParent = pCur;
pCur = pCur->_pLeft;
}
else
{
pParent = pCur;
pCur = pCur->_pRight;
}
}
// data不在二叉搜索树中,无法删除
if (nullptr == pCur)
return false;
// 分以下情况进行删除,同学们自己画图分析完成
if (nullptr == pCur->_pRight)
{
// 当前节点只有左孩子或者左孩子为空---可直接删除
}
else if (nullptr == pCur->_pRight)
{
// 当前节点只有右孩子---可直接删除
}
else
{
// 当前节点左右孩子都存在,直接删除不好删除,可以在其子树中找一个替代结点,
比如:
// 找其左子树中的最大节点,即左子树中最右侧的节点,或者在其右子树中最小的节
点,即右子树中最小的节点
// 替代节点找到后,将替代节点中的值交给待删除节点,转换成删除替代节点
}
return true;
}
// 自己实现
void InOrder();
private:
PNode _pRoot;
};四、二叉搜索树的应用
在我们目前的学习中,二叉搜索树最重要的用途就是key--val模型,KV模型就是每一个key值都对应一个val值,这样就形成一个<key,val>键值对,这样的应用在生活中是非常常见的
比如:在菜市场中不同的蔬菜对应着不同的价格;新华词典中,不同的汉字对应着不同的拼音,这些都可以用KV模型来解决
下面是KV模型的实现(没有主函数):
namespace kv
{
template<class K,class V>
struct BSTreeNode
{
BSTreeNode<K,V>* _left;
BSTreeNode<K,V>* _right;
K _key;
V _value;
BSTreeNode(const K& key,const V& value)
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template<class K,class V>
class BSTree
{
typedef BSTreeNode<K,V> Node;
public:
//遍历(中序)
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_InOrder(root->_right);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
///
bool Insert(const K& key,const V& value)
{
if (_root == nullptr)
{
_root = new Node(key,value);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
parent = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key,value);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 准备删除 20:15继续
if (cur->_left == nullptr)
{//左为空
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{//右为空
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else
{//左右都不为空
// 右树的最小节点(最左节点)
Node* parent = cur;
Node* subLeft = cur->_right;
while (subLeft->_left)
{
parent = subLeft;
subLeft = subLeft->_left;
}
swap(cur->_key, subLeft->_key);
if (subLeft == parent->_left)
parent->_left = subLeft->_right;
else
parent->_right = subLeft->_right;
delete subLeft;
}
return true;
}
}
return false;
}
BSTree() = default;
~BSTree()
{
Destroy(_root);
}
//递归版本
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool FindR(const K& key)
{
return _FindR(_root, key);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
BSTree(const BSTree<K,V>& t)
{
_root = Copy(t._root);
}
BSTree<K,V>& operator=(BSTree<K,V> t)
{
swap(_root, t._root);
return *this;
}
private:
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newroot = new Node(root->_key);
newroot->_left = Copy(root->_left);
newroot->_right = Copy(root->_right);
return newroot;
}
void Destroy(Node*& root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
root = nullptr;
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
if (root->_left == nullptr)
{
root = root->_right;
return true;
}
else if (root->_right == nullptr)
{
root = root->_left;
return true;
}
else
{
Node* subLeft = root->_right;
while (subLeft->_left)
{
subLeft = subLeft->_left;
}
swap(root->_key, subLeft->_key);
return _EraseR(root->_right, key);
}
}
}
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key < key)
{
return root->_right;
}
else if (root->_key > key)
{
return root->_left;
}
else
{
return true;
}
}
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}
Node* _root = nullptr;
};
}
五、总结
以上就是二叉搜索树的主要内容,在代码实现上其实与之前讲的二叉树差别并不是很大,关键在于思路的梳理,这章就先到这了

感谢各位大佬观看,创作不易,还请各位大佬点赞支持!!!