一、介绍

匿踪查询：一个客户从服务器查询数据，并且服务器无法知晓查询内容。注意这里是保护查询安全，并不保护服务器数据安全。

主要贡献：

        1.设计了一款更高速度的匿踪查询方案。

        2.设计一款支持批量查询的匿踪查询方案。

        3.匿踪方案可以拓展并支持labelPSI。

        4.全面的实验评估和分析。

二、背景知识

1.Homomorphic encryption（同态解密）

本文中使用的为FHE加密算法，详细的原理可以参考LWE，这里有几个原理需要知晓：

1)解密X ← SIMDEnc(pk, x). 一个向量：X = [x1, ..., xN ]会被加密到一个密文中X。

2)解密X ← SIMDDec(sk, ex). 

3)Z ← SIMDAdd(X, Y).加法同态。

4)Z ← SIMDMul(X, Y).乘法同态。

5)X' ← SIMDRotate(X, c). 密文内部旋转，比如原本X解密结果为[1,2,3,4,5]，若c=2，X'解密结果为[3,4,5,1,2]。

这种加密方式可以实现一次密文乘获得该密文中所有位置密文对应明文是否相等的等值判断。

2.Constant-weight code and CwPIR(定权重编码)

所有数据编码成固定形式的码值，比如：

3.Batch code（批量编码）

理解为一种分桶技术，B=1.5L，每个桶执行一次查询，最终能恢复L个数据，可以小于L。

三、技术方案

单条查询——小数据量

1.预处理

将数据库拆分成N*t的矩阵，N为多项式模数即4096或8192。

2.query生成

首先确定想要查询的行号和列号，比如N+2的位置即2行2列，首先对生成N行全零数据，但是第2行数据为2的定全码：

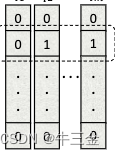
将这些数据进行加密，并发送给数据方，

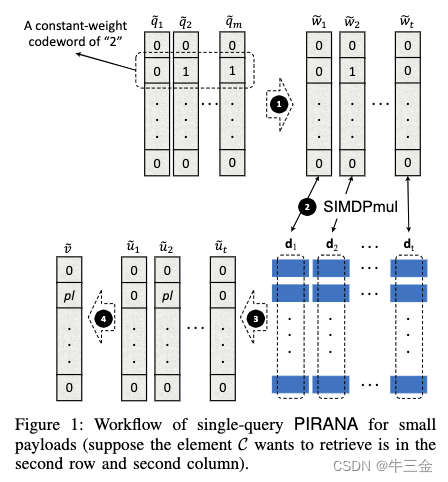
数据方根据获得的Q进行计算W，即图中第一步，这个图解释一下：

• 先看右下角的d_1～d_t，是将数据进行切分，切分成N·t的数据矩阵。
• 看图右上角，数据方本地通过定编码计算y，比如y_2=[0,0,0,0,0....,1,1]，然后计算q_m-1和q_m的乘积，计作W_2，以此类推计算剩下内容。
• 使用W乘以对应的D，获得数据密文结果U。然后让所有U相加即可。

3.解密

查询方获取密文解密即可。

单条查询——大数据量

假设每条数据大于256bit，刚才图中的d的每个蓝色位置，不能存放一条完整数据。

简单的做法：将每条数据切分，也就是创建多个数据矩阵，不够的用空填充，然后进行上门的逻辑多次，可以获得多个密文结果，然后解密之后数据拼接即可。

这种方式会发现通信开销过大，这里我们可以获得多个V，但是其中有大量的0，这些其实是空间浪费，如何填充进去呢，我们可以向后旋转一位，然后相加。

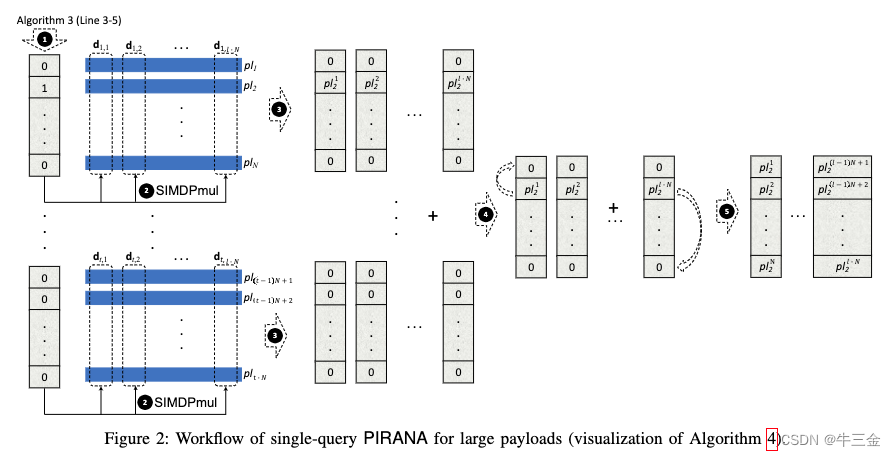
多关键词查询：

上文中我们提到过Batch code（批量编码）的分桶技术，这里数据方首先将自身数据进行分桶，将一个数据集分桶成m个，然后基于每个桶进行匿踪查询，将获得一个结果，我们根据Batch code技术可以很简单的获得想要查询的任意数据。

四、总结

本文介绍了一款匿踪查询方式，其思路结合了编码技术（与sealPir相似），同态旋转技术（与vectorPir相似），该论文对于多关键词查询提供了一个思路，但是对于超大数据库场景还是不能很好的支持，在现实的工业场景中还是需要进一步考虑亿级数据库不可数据预处理的问题。

参考
《PIRANA: Faster Multi-query PIR via Constant-weight Codes》https://eprint.iacr.org/2022/1401.pdf哔哩哔哩https://www.bilibili.com/video/BV1Zw4m1e7dm/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=a6ba350c9fafb216edd3eb26c8efbf55