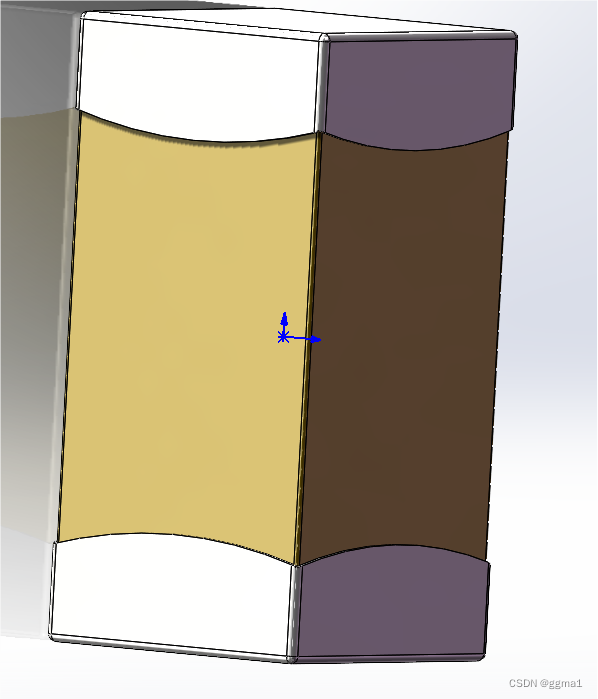
这个问题可以通过计算最大公约数 (GCD) 和最小公倍数 (LCM) 来解决。我们需要找到一个整数,它是 a, b, c 的 GCD 的倍数,同时也是 d, e, f 的 LCM 的约数。
以下是解决这个问题的步骤:
1. 计算 a, b, c 的最大公约数。
2. 计算 d, e, f 的最小公倍数。
3. 检查是否存在一个整数,它是步骤 1 中得到的 GCD 的倍数,同时也是步骤 2 中得到的 LCM 的约数。
以下是实现这个算法的 C++ 代码:
#include <iostream>
#include <algorithm>
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
int lcm(int a, int b) {
return a / gcd(a, b) * b;
}
int main() {
int a, b, c, d, e, f;
while (std::cin >> a >> b >> c >> d >> e >> f && (a || b || c || d || e || f)) {
int gcd_abc = gcd(gcd(a, b), c);
int lcm_def = lcm(lcm(d, e), f);
if (lcm_def % gcd_abc == 0) {
std::cout << "YES" << std::endl;
} else {
std::cout << "NO" << std::endl;
}
}
return 0;
}这段代码首先定义了两个函数:gcd 和 lcm,分别用于计算两个数的最大公约数和最小公倍数。然后在主函数中,我们读取输入,计算 a, b, c 的最大公约数和 d, e, f 的最小公倍数,然后检查是否存在一个整数,它是最大公约数的倍数,同时也是最小公倍数的约数。如果存在,我们输出 "YES",否则输出 "NO"。



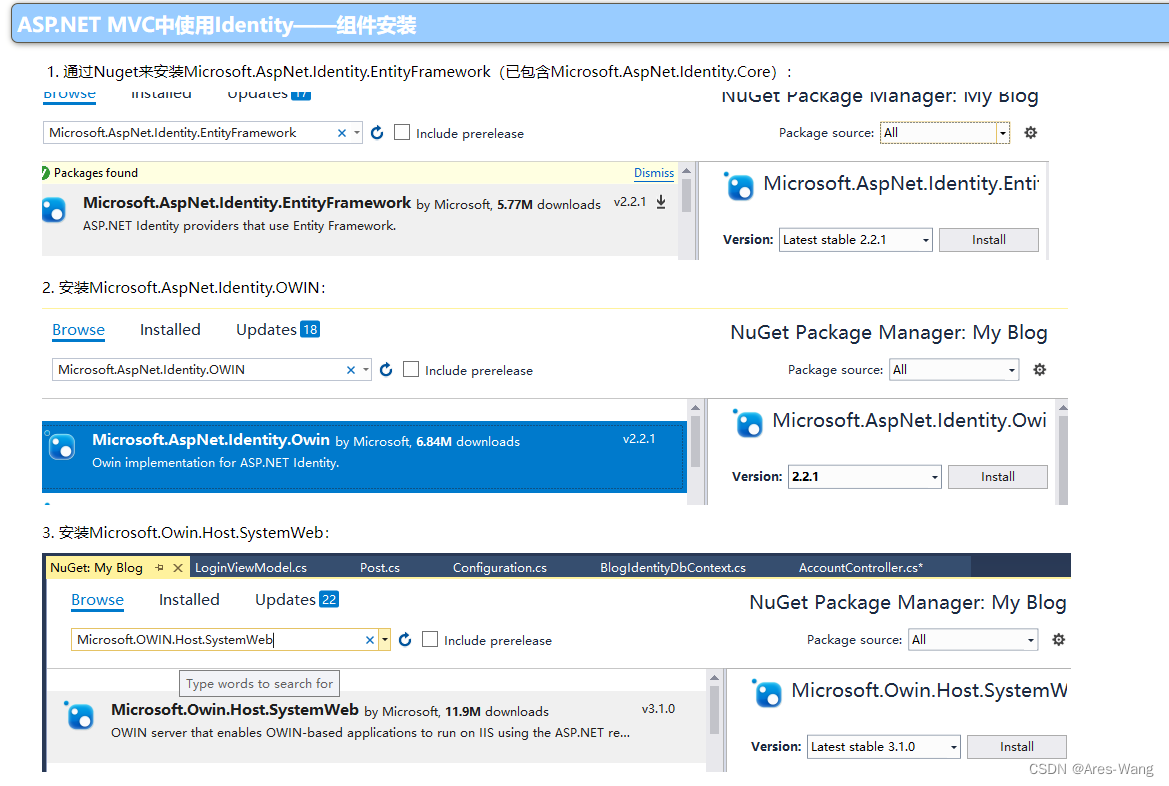



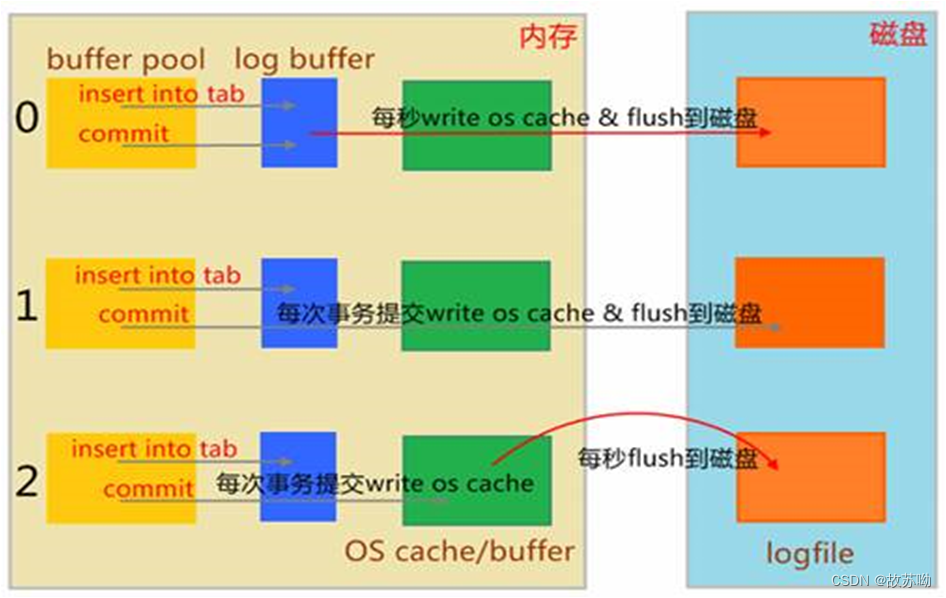

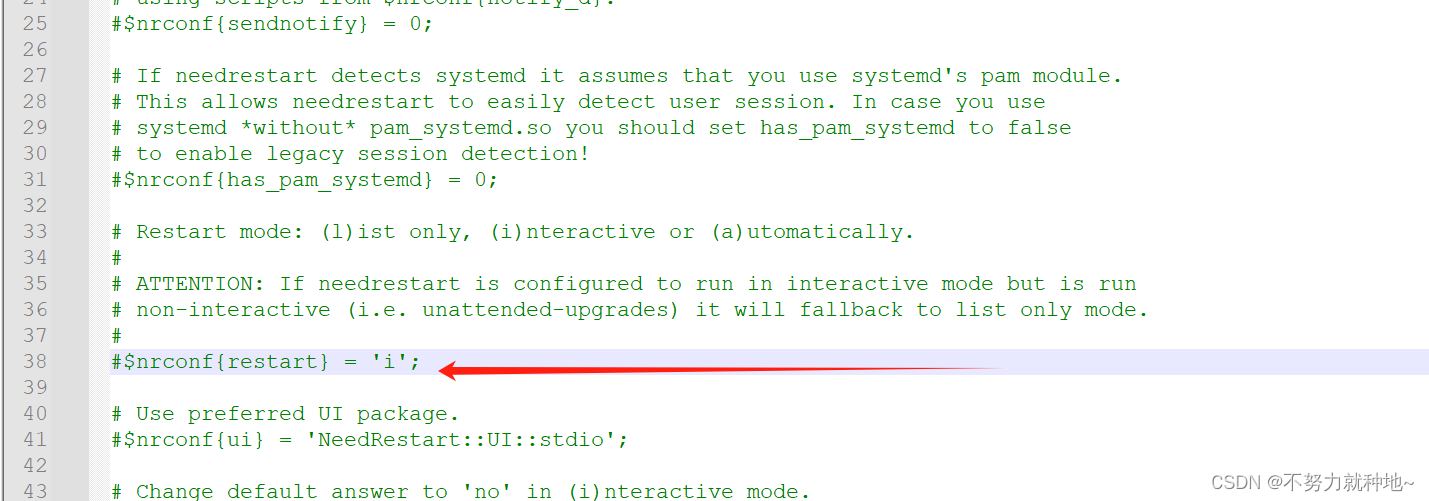



![[图解]企业应用架构模式2024新译本讲解19-数据映射器1](https://img-blog.csdnimg.cn/direct/05e3e288c26f449382203e8ef47f3e68.png)