大纲
贝尔曼最优公式是贝尔曼公式的一个特殊情况,但其也非常重要。
本节课很重要的两个概念和一个工具:

工具不用多说,就是贝尔曼最优公式,概念则是 optimal state value(最优状态价值) 和 optimal policy(最优策略)。
本节课课程大纲:

Motivating examples
之前已经举过的例子:

箭头是策略,也就是 Π,对于这个例子要做的事情其实就是求解贝尔曼公式得到 state value,进而得到 action value,而在这个基础之上呢我们会再介绍一个很有意思的现象。
上图中已经算出了 state value,那么接下来可以根据 state value 来获得 action value:

那么接下来有一个问题,如果当前这个策略是不太好的,我们怎么去提升它呢?
答案就是依赖 action value:

从刚刚的计算过程当中不难发现,当采取 action 为 a3 的时候,其 action value 是最大的,那么我们就可以选择 a3 来作为一个新的策略:

为什么我们刚刚选择 action value 最大的那个 action 就能够得到一个比较好的策略呢?:
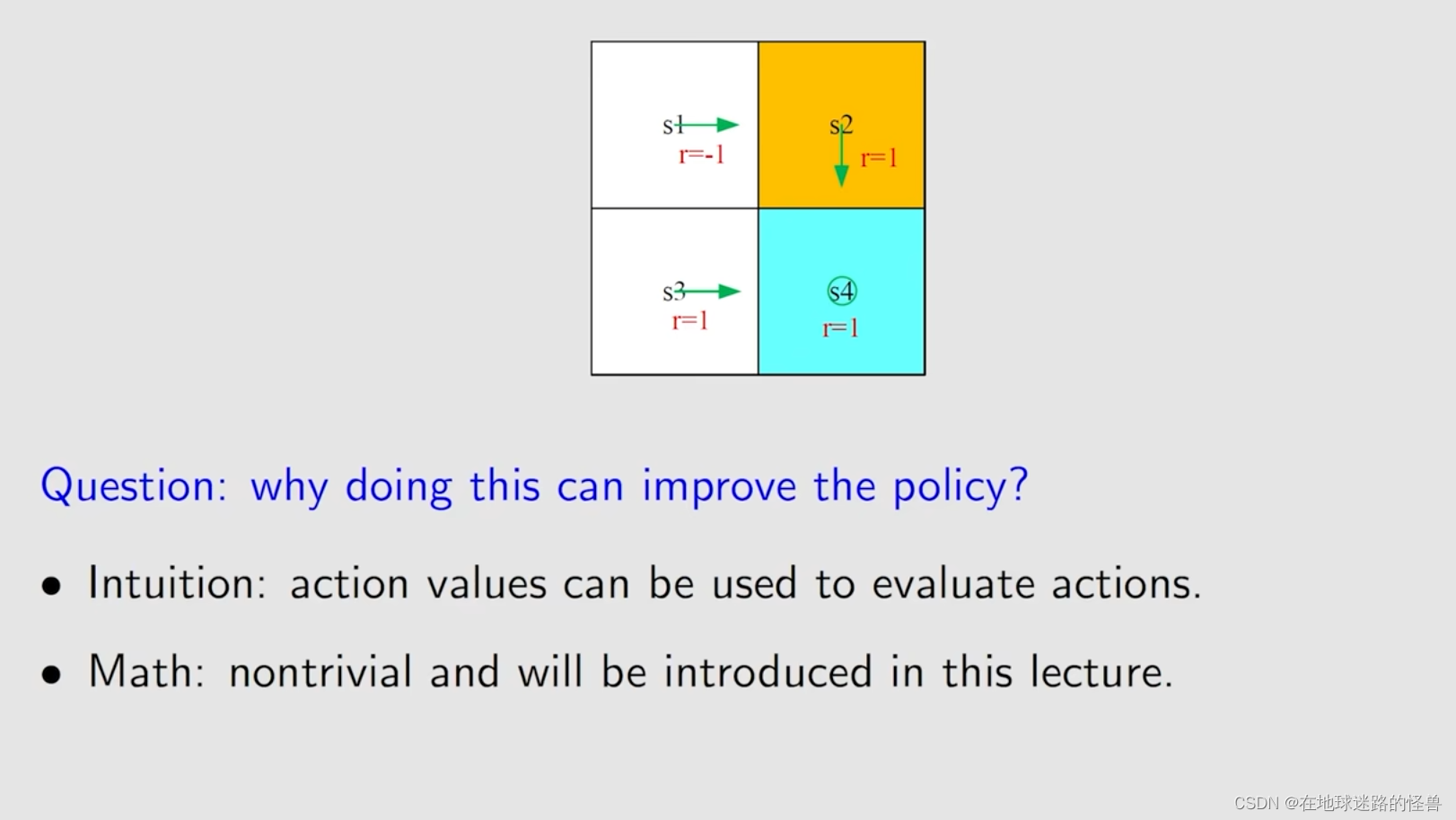
什么时候都能得到最优的 action 吗?显然是肯定的,只要我们不断的去这样做(计算 action value 然后取value 最大的 action),不断地迭代,最后一定会得到一个最优的策略。
也就是说对于每一个状态我们都选择 action value 最大的那个 action,选择完一次后再来一次迭代得到一个新的策略再迭代得到一个新的策略,最后那个策略就会趋向一个最优的策略。
而这实际上这个过程已经超出了上图中的这种比较直观的理解,有必要依赖于数学来进行更严格的更透彻的分析,而这个数学的工具就是贝尔曼最优公式。
Definition of optimal policy
开始正式的定义 最优策略。

定义并不麻烦,关键是定义之后需要回答一系列问题,即上图中的问题,而要解决这些问题则可以通过研究贝尔曼最优公式进行解决。
BOE:Introduction
首先直接给出 贝尔曼最优公式,然后再详细分析它的性质。

最优公式与一般公式其实很相似,就是在策略 Π 前面限定了一个 max Π,此时就嵌套了一个优化问题,我们需要先解决这个优化问题,求解出来这个 Π,然后再把这个 Π 代入到这个式子里面去进行求解。
上图中的一个问题,就是 BOE 中这个 Π 是已知的还是未知的?
对于一个贝尔曼公式来说,其一定是依赖于一个给定的 Π ,但是贝尔曼最优公式是没有给定的,我们必须要去求解这样一个 Π 。


BOE:Maximization on the right-hand side

上图的绿色框中举了一个简单的例子来进行说明如何求解一个表达式中有两个未知数的问题,那么接下来通过从这个例子中获得的启发来解决贝尔曼最优公式中求解最优策略 max Π ,在这儿先要提一点,就是对于公式中的 V 一撇,通常情况下我们会先给一个初始值,所以在给定初始值时那么 V 一撇实际上也是给定的已知项:

在本课程设定的网格世界中,因为 action 有多个,所以 action value 也会有多个,在 q(s, a) 已知的情况下有q(s, a1)、q(s, a2) … q(s, a5),有这样五个值,那么怎么求解 max Π 呢?
而上图中绿色框部分的内容给了我们一定的启发,即如果 q(s, a) 值确定的话我们怎么样来求解最优的策略 Π :

BOE:Rewrite as v = f(v)
实际上我们可以把等式右边的这一串式子给写成一个函数:

因为我们要求解的 max Π 的方法是先固定 v 那么就可以求出来一个 Π,至于这个 Π 是什么样子,最后得到的最优的值是什么其实不用太关心,反正其肯定是关于 v 的一个函数。
因此贝尔曼最优公式就化成了 v = f(v)。
在求解这个式子之前,我们需要先介绍一下 Contraction mapping theorem 。
Contraction mapping theorem(压缩映射定理)

先来介绍 fixed point 和 contraction mapping 的概念:

下面是两个例子:

有了上面两个概念之后就可以引出 contraction mapping theorem(压缩映射定理):

意思就是对于一个式子:x = f(x),压缩映射定理告诉我们三个重要的结论:
1、existence:我们并不关心函数 f 它的表达式是什么,它只要是一个 contraction mapping,我们就能够确定它一定存在一个 fixed point 满足 f(x*) = x*;
2、uniqueness:我们还能确定这个 fixed point 是唯一存在的;
3、Algorithm:我们还能知道怎么样去解决这样一个 fixed point 。
两个例子再来感受一下这个定理:

BOE:Solution
在有了压缩映射定理的帮助之后,我们就可以进行 BOE 的求解了。
但是在应用压缩映射定理之前呢,我们需要证明这里面的 f(v) 其是一个 contract mapping:

在已知 f 是一个 contraction mapping 之后,那么贝尔曼最优公式就可以立刻用 contract mapping theorem 来求解出来:

由之前的内容可知,贝尔曼最优公式它一定存在一个唯一解,用 v* 来表示,然后可以使用上图中的迭代表达式迭代地求解出来,而这个 Vk 最后会收敛到这个 v*。
BOE:Optimality
分析一下贝尔曼最优公式的解的最优性。

经过上图的转换,最后能够化成一个贝尔曼公式,而贝尔曼公式一定是对应到一个策略的,那么这个就是对应 Π* 的这样一个贝尔曼公式。自然这里面的 v* 也就是 vΠ* 也就是 Π* 所对应的 state value。
因此贝尔曼最优公式是一种特殊的贝尔曼公式,其对应的策略是比较特殊的,其对应的是一个最优的策略。
对应这个策略是不是最优的,state value 值是不是最大的,是可以使用数学进行严格证明的:

Π* 的样子:

Analyzing optimal policies
使用 BOE 来分析一些最优的策略,看看都有哪些有趣的性质。

系统的模型是很难改变的,因此我们不考虑,只考虑修改 reward 和 γ 折扣率 来看一下这两个因素是怎样影响最优策略的。
下面是一个例子:
先来看看修改折扣率会是个什么样的情况:

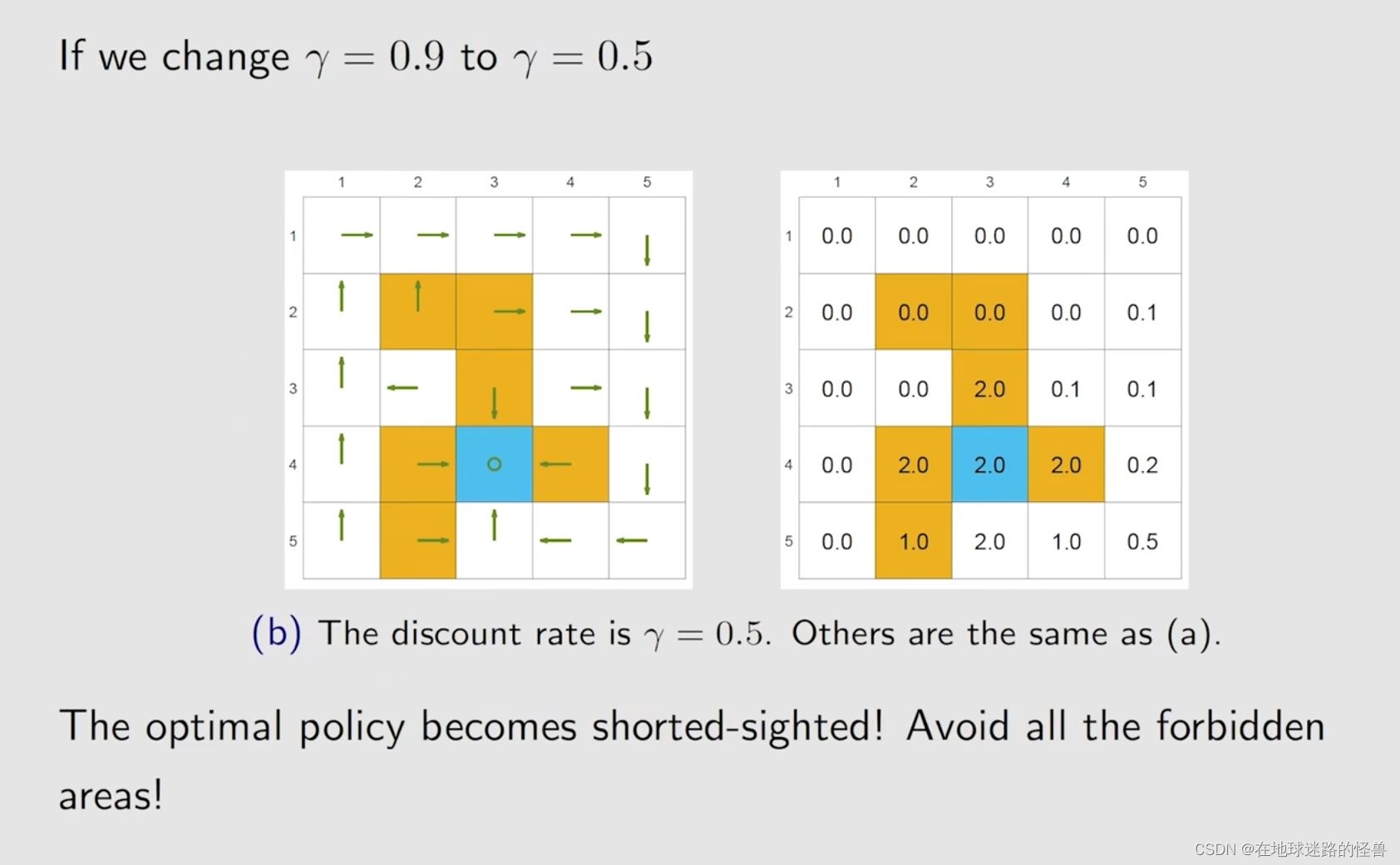

接下来再来看看修改 reward 会造成的影响:

接下来考虑另一种特殊且重要的情况:

可以看到如果做了这种线性的变换,最后的最优策略实际上是不会改变的,因为最重要的其实不在于这个 reward 的绝对值是多大,而是在于它们互相之间的这种相关价值(relative value)。
这样的结果同样可以数学证明:

还有一种情况,就是 meaningless detour 的情况(绕远路),很多人会觉得,agent 每走一步就应该给它一个惩罚,比如说 r = -1,那实际当中这个 r = -1 就代表一种能量的消耗,这样的化 agent 就不会绕远路,就会尽可能的走最短的路径到目标区域。
那如果 r = 0 的话,没有 r = -1 的话那好像它就会绕远路?但实际上不是这样的,因为除了 reward 来约束 agent 不要绕远路之外,我们还有 γ 折扣率来进行约束。因为它越绕远路就越意味着我们得到到达目标的奖励越晚,越晚那时候对应的 γ 的次方就越小,打折会打得越厉害,那么自然其就会找一个最短的路径过去。
Summary
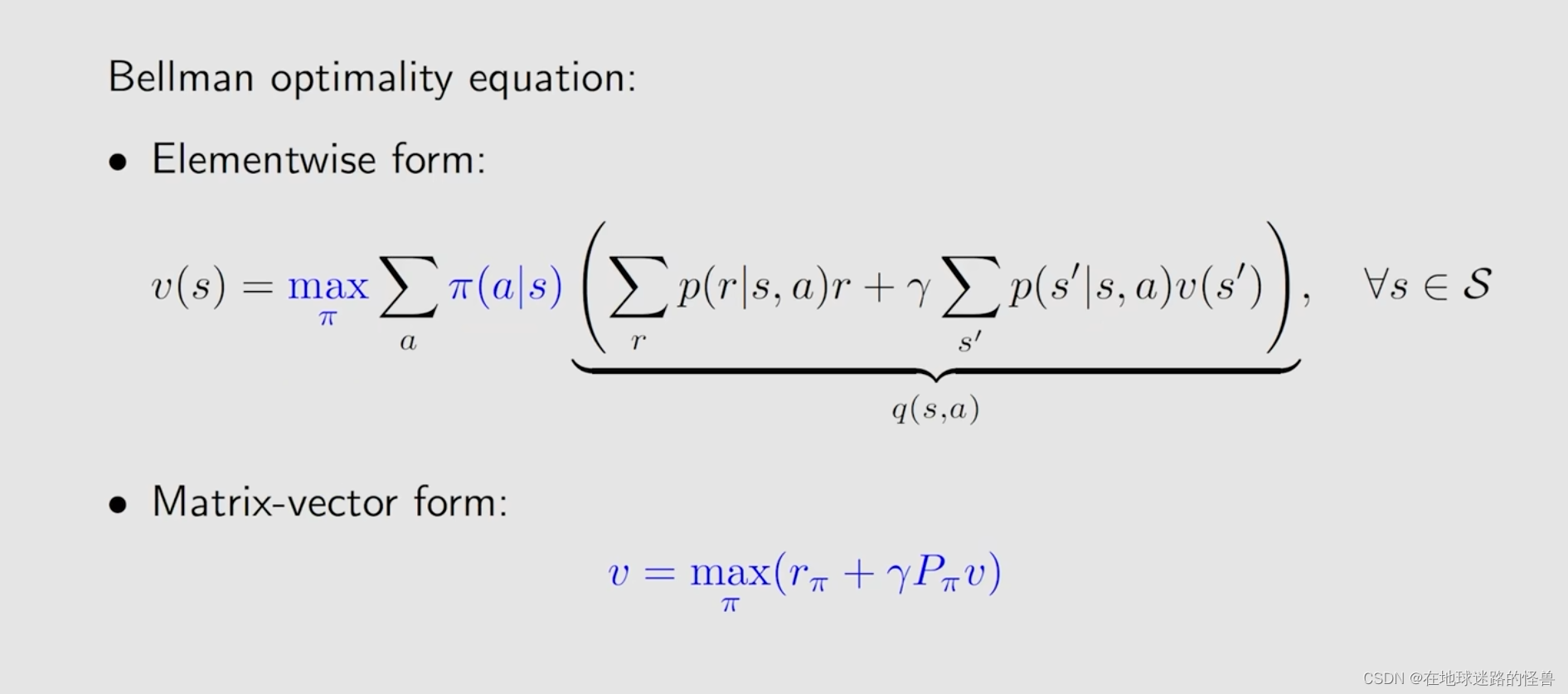







![[图解]企业应用架构模式2024新译本讲解19-数据映射器1](https://img-blog.csdnimg.cn/direct/05e3e288c26f449382203e8ef47f3e68.png)