概述

语言模型的发展

语言模型经历过四个阶段的发展，依次从统计语言模型到神经网络语言模型（NLM），到出现以 BERT 和 Transformer 架构为代表的预训练语言模型（PLM），最终到大型语言模型阶段（LLM）。

NLM

使用神经网络（如循环神经网络RNN、长短时记忆网络LSTM等）来构建语言模型。这些模型通过学习输入文本序列，预测下一个单词或字符的概率分布

PLM阶段

大规模的未标注文本语料库上进行无监督预训练，学习通用的语言结构和表达。

LLM阶段

大型语言模型通常指的是具有极大量参数的预训练模型，如几千亿甚至上万亿参数。这些模型由于其庞大的规模，能够学习到更加丰富和精细的语言结构和知识

LLM的训练与推理流程

语言模型能把人类语言的字符转换成机器能够识别的序列，这些序列要通过位置编码来标记文本的前后顺序，再把序列输入到具体的算法模型中，模型的输出是归一化的token概率，
例如GPU平台的计算过程，将权重数据从显存（HBM）加载至on-chip的SRAM中，然后由SM读取并进行计算。计算结果再通过SRAM返回给显存。

embeding

指将某种类型的输入数据（如文本、图像、声音等）转换成一个稠密的数值向量，以便计算机能够识别和处理。
这些向量通常包含较多维度，每一个维度代表输入数据的某种抽象特征或属性。

推理过程

LLM的推理过程分为两个阶段，prefill（预填充）和decode（解码）。
预填充阶段会把整段prompt喂给模型做forward计算，
解码阶段即通过KV值计算attention，该阶段的耗时比较大

相关研究

训练相关

推理相关

LLM的推理分为两个阶段：prefill和decode

知乎：手抓饼熊：大模型推理加速系列分享

基于GPU的加速

知乎：猛猿：图解大模型计算加速系列：FlashAttention V1，从硬件到计算逻辑

Transformer

谷歌在2017年的论文《Attention Is All You Need》¹提到了 Transformer 模型框架。模型提到了“自注力”（self-attention）机制，

基本架构

如图是 Transformer 模型架构图，该架构分为左侧的编码器和右侧的解码器，编码器将新的输入字符序列映射成连续特征序列，解码层每次产生一个字符的输出序列，每次模型将自动递归，每产生下一个字符输出序列时，消耗之前产生的字符作为额外输入。

输入和输出

Inputs：新的字符输入通道，将位置编码向量与词嵌入相加，得到带有位置信息的输入向量：
$X_{pos}=E_{pos}+P{E}_{pos}$

$E_{pos}$是第pos个词的词嵌入向量，$P{E}_{pos}$是位置pos的位置编码向量。

Ouputs（shifted right）：上一次的输出序列
Ouput Probabilities：输出序列

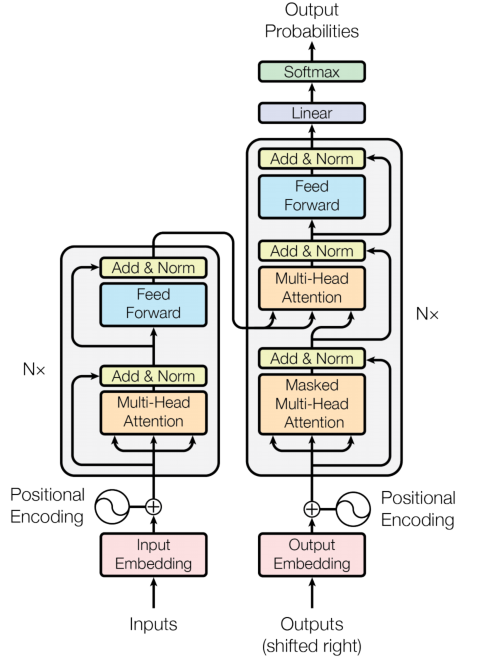
Encoder

包含6个识别层，每个识别层都有两个子层。
第一层时多头自注力机制层，第二层时一个简单的位置识别的全连接前馈神经网络。

Decoder

自注力机制

能够把单一序列的不同位置联系起来，从而能计算出这个序列的含义。

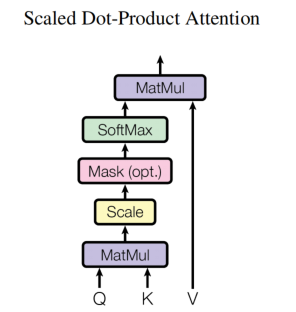
Scaled Dot-Product Attention

$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$

Q，K，V 据论文描述是 Query、Key 和 Value 单词的缩写， $K^T$是K的转置。

$Q=X{W}_Q$
$K=X{W}_K$
$V=X{W}_V$
$X\in {\mathbb{R}}^{batch\_size\ast se{q}_{l}en\ast embed\_dim}$，表示输入数据
$W_V、W_K、W_Q\in {\mathbb{R}}^{embed\_dim\ast embed\_dim}$，表示三个参数的权重

$Q{K}^T$可以理解为词向量的接近程度，详细可参考该文²的第4章节。
除以$\sqrt{d_k}$是为了把$Q{K}^T$矩阵变成标准正态分布，使得softmax归一化之后的结果更加稳定，以便反向传播的时候获取平衡的梯度。

softmax的计算

Softmax 函数是一种将一个 K 维实数向量（或矩阵的最后一维）转化为一个归一化概率分布的函数。在机器学习和深度学习中，尤其是在多分类问题中，softmax 函数常常被用作输出层的激活函数，将模型预测的原始得分转换为概率值。
即对于一个K维向量$z=[z_1,z_2,...,z_K]$，则softmax的输出向量s为：
$$s_j=\frac{e^{z_j}}{{\sum }_{k=1}^K{e}^{z_k}}$$

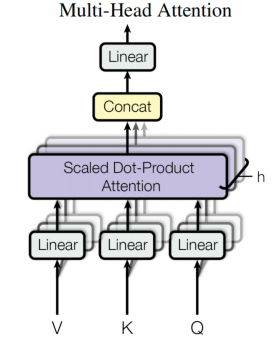
Multi-Head Attention

如图所示，V、K、Q经过Linear拆分后，得到heads个矩阵，每个结果都经过上述Scaled Dot-Product Attention计算，最后通过Concat拼接起来，最后再作Linear操作。

$MultiHead(Q,K,V)=Concat(hea{d}_1,...,hea{d}_h)W^O$
其中$hea{d}_i=Attention(Q{W_i}^Q,K{W_i}^K,V{W_i}^V)$

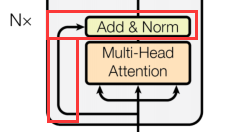
残差连接

如下图所示，将Multi-Head Attention的输入和输出连接，继而累加，即为残差连接。这样引入捷径的方式，使得信息能够更快的bypass地穿过深层网络，从而改善模型地训练效果和性能。

层归一化

在残差连接计算后，需要对结果归一化处理，从而改善模型中地梯度传播问题，进而提高模型地训练效率和性能。具体计算方式：
对于矩阵每一行x，计算器均值$\mu$和方差${\sigma }^2$
$$\mu =\frac{1}{m}\sum _{i=0}^{n-1}{x}_i$$
$${\sigma }^2=\frac{1}{m}\sum _{i=0}^{n-1}(x_i-\mu {)}^2$$
归一化地处理如下，其中$ϵ$是一个较小地常数， $\gamma$和$\beta$是标量参数，通过反向传播和梯度下降学习：
$$LayerNorm(x)=\gamma \frac{x_i-\mu }{\sqrt{{\sigma }^2+ϵ}}+\beta$$

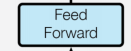
前馈神经网络（FFN）

FFN是一个全连接的前馈神经网络结构，内部结构包括两个线性变换层，中间插入一个非线性激活函数。

第一层线性变换

将自注力机制的输出结果记为$X$，通过一个线性映射将输入转换成新的向量表示：
$$H=W_{1}X+b_1$$
并通过ReLU激活函数进行非线性处理：
$$H^{{}^{\prime }}=ReLU(H)$$

第二层线性变换

对ReLU激活后的向量$H^{{}^{\prime }}$再次进行线性映射：
$$FFN(X)=W_2{H}^{{}^{\prime }}+b_2$$

计算特征

参考该文的第二章节，从attention计算的不同流程分析了两种限制：计算限制和内存限制。
图解大模型计算加速系列：FlashAttention V1，从硬件到计算逻辑

输入位置编码向量与词嵌入相加

浮点数的加法操作

自注力矩阵的计算

$Q{K}^T$的矩阵乘计算，$\sqrt{d_k}$的根号运算，以及两个结果相除计算
再将结果进行softmax函数计算，包括乘法、求和、除法运算。
$softmax(\frac{Q{K}^T}{\sqrt{d_k}})$

multi-Head Attention的conact和linear操作

残差求和操作

层归一化

平均数求和和除法操作
求方差操作
归一化处理（求差、除法等）

FFN的两级线性乘加运算

参考文献

---

1. Google:《Attention Is All You Need》 ↩︎

2. 知乎：大模型背后的Transformer模型究竟是什么？ ↩︎