摘要  计算机的错误计算（四）指出一元二次方程的计算精度问题。本节给出其一种解决方案。

       计算机的错误计算（四）与（十七）分别指出一元二次方程的求解是具有挑战性的难题，其出错原因是因为相减相消而导致损失了精度。

       下面我们仔细分析。

       一元二次方程      的求根公式为

       当   时， 与  会很接近，这样，  中一个运算就会发生相减相消。

       比如，若 , 则   有相减相消发生；相反，若  , 则   会发生相减相消。 相减相消的根源在于“相减”，那么如何去掉这个“相减”呢？若您中学数学学得好，不难想到，用公式    即分子分母同乘以   （这时是同号的两数相加），让“分子有理化” ： 

       上式就是一种很好的解决方案。它没有增加计算量或复杂度。

例1.  （续计算机的错误计算（四）的例1）已知 ，计算其较小的根。

       显然，由于

 

因此较小的根   会发生相减相消。

       现在，利用新的公式   编程如下：

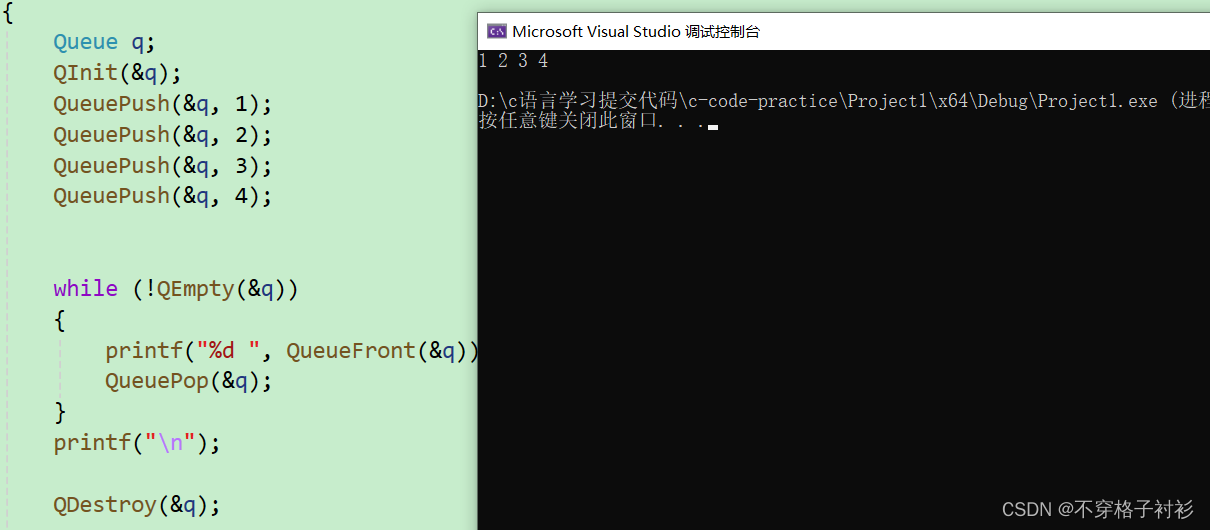
在 Visual Studio 2010 中运行它，则输出为正确结果1。

       最后，问一句：任给一个可能发生相减相消的算式，若找不到对应的替代公式怎么办？去不掉相减相消该怎么办？

       答案是：采用高精度计算。那么问题又来了，高到多少？很简单：损失多少，增加多少。

       若遇到了，不知结果对不对，不妨先在这里试试（这个是万能的，任何算术表达式都能得出正确结果。后面有机会再介绍）：ISReal 计算器, 可信计算http://www.isrealsoft.cn/