【Python实战因果推断】12_线性回归的不合理效果2

news2024/11/17 19:30:56

Adjusting with Regression

为了了解回归的威力，让我带您回到最初的例子：估计信贷额度对违约的影响。银行数据通常是这样的，其中有很多列客户特征，这些特征可能表明客户的信贷价值，比如月工资、征信机构提供的大量信用评分、在当前公司的任职期限等等。然后是给予该客户的信贷额度（本例中为干预），以及告诉您客户是否违约的列--结果变量：

 risk_data = pd.read_csv("./data/risk_data.csv")
 risk_data.head()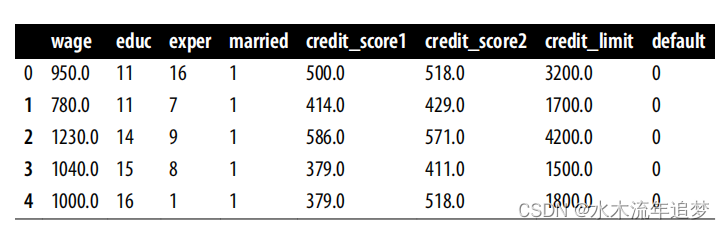

在这里，干预变量 credit_limit 的类别太多了。在这种情况下，最好将其视为连续变量，而不是分类变量。与其将 ATE 表示为多级处理之间的差异，不如将其表示为预期干预结果相对于处理结果的导数： $ATE=\frac{\partial}{\partial t}E[y|t]$

别担心这听起来很花哨。它简单地说，就是在干预增加一个单位的情况下，您预计结果会发生变化的金额。在本例中，它表示在信贷额度增加 1 美元的情况下，您预计违约率会发生多大变化。估算这种数量的一种方法是进行回归。具体来说，您可以估计以下模型

$Default_i=\beta_0+\beta_1\text{limit}_i+e_i,$

而估计值 β1 可以解释为限额增加 1 美元时，您预期风险会发生的变化。如果限额是随机的，那么这个参数就具有因果关系。但大家都很清楚，情况并非如此，因为银行倾向于给风险较低的客户更高的额度。事实上，如果运行前面的模型，您会得到 β1 的负估计值。

 model = smf.ols('default ~ credit_limit', data=risk_data).fit()
 model.summary().tables[1]

这一点也不奇怪，因为风险与信用额度之间的关系是负相关的。如果将拟合回归线与按信用额度计算的平均违约率并列，就可以清楚地看到负趋势：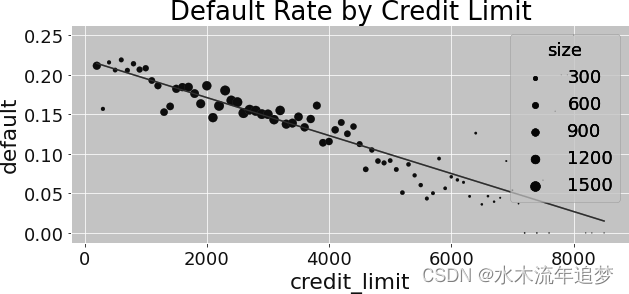

理论上，为了调整这种偏差，您可以按照所有混杂因素对数据进行分段，在每个分段内运行违约对信用额度的回归，提取斜率参数，然后求平均值。然而，由于维度的限制，即使您尝试对中等数量的混杂因素（包括信用评分）进行分段，您也会发现有些单元格只有一个样本，因此无法进行回归。更不用说还有很多单元格是空的了：

 risk_data.groupby(["credit_score1", "credit_score2"]).size().head()
 
Out[6]: credit_score1 credit_score2
 34.0 339.0 1
 500.0 1
 52.0 518.0 1
 69.0 214.0 1
 357.0 1
 dtype: int64

值得庆幸的是，回归方法再次为您提供了帮助。您无需手动调整混杂因素，只需将其添加到用 OLS 估计的模型中即可：

$Default_i=\beta_0+\beta_1\mathrm{limit}_i+\theta\mathbf{X}_i+e_i,$

这里，X 是混杂变量的向量，θ 是与这些混杂变量相关的参数向量。θ参数并无特别之处。它们的行为与 β1 完全一样。我之所以用不同的方式来表示它们，是因为它们只是用来帮助你得到 β1 的无偏估计值。也就是说，你并不真正关心它们的因果解释（严格来说，它们被称为干扰参数）。

以信贷为例，您可以在模型中加入信贷评分和工资混杂因素。它看起来是这样的

$Default_{i}=\beta_{0}+\beta_{1}\mathrm{limit}_{i}+\theta_{1}\mathrm{wage}_{i}+\theta_{2}\mathrm{creditScore}1_{i}+\theta_{3}\mathrm{creditScore}2_{i}+e_{i},$

我会详细介绍在模型中加入变量如何调整混杂因素，但现在有一个非常简单的方法。前面的模型是 $E[y|t,X]$ 的模型。那么，如果将该模型与干预-信贷限制进行微分，会发生什么呢？那么，你只需得到 β1！

从某种意义上说，β1 可以看作是违约预期值对信贷额度的偏导数。或者，更直观地说，可以把它看作是在模型中所有其他变量保持不变的情况下，当信用额度略有增加时，违约的预期值会有多大变化。这种解释已经告诉我们回归是如何调整混杂因素的：在估计干预与结果之间的关系时，它将混杂因素保持不变。

要想了解这一点，您可以对前面的模型进行估计。只要添加一些混杂因素，就会像变魔术一样，信贷额度和违约之间的关系就会变成正相关！

 formula = 'default ~ credit_limit + wage+credit_score1+credit_score2'
 model = smf.ols(formula, data=risk_data).fit()
 model.summary().tables[1]

不要被 β1 的微小估计值所迷惑。回想一下，限额是以 1,000 为单位的，而违约是 0 或 1。因此，增加 1 美元的额度会使预期违约率上升一个很小的数字，这并不奇怪。尽管如此，这个数字在统计学上还是很有意义的，它告诉你风险会随着信用额度的增加而增加，这更符合你对世界运行方式的直觉。

请稍安勿躁，因为你将对它进行更正式的探讨。终于到了学习最伟大的因果推理工具之一：弗里施-沃-洛威尔（FWL）定理的时候了。这是一种令人难以置信的消除偏差的方法，但遗憾的是，数据科学家很少了解这种方法。FWL 是了解更高级去偏差方法的先决条件，但我认为它最有用的原因是，它可以用作去偏差的预处理步骤。还是以银行业为例，想象一下这家银行的许多数据科学家和分析师都在试图了解信用额度如何影响（导致）许多不同的业务指标，而不仅仅是风险。然而，只有您才掌握信用额度是如何分配的，这意味着您是唯一知道信用额度干预存在哪些偏差的专家。有了 FWL，您就可以利用这些知识对信用额度数据进行去伪存真，使其他人也能使用这些数据，无论他们对什么结果变量感兴趣。Frisch-Waugh Lovell 定理允许您将去伪存真步骤与影响估计步骤分开。但要学习它，你必须先快速回顾一下回归理论。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1884418.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！