支持我的工作 🎉
如果您想看到更详细、排版更精美的该系列文章,请访问:2022吴恩达机器学习Deeplearning.ai课程作业
可选实验:特征工程和多项式回归
目标
在本次实验中,你将:探索特征工程和多项式回归,这将允许你使用线性回归的工具来拟合非常复杂,甚至是非常非线性的函数。
import numpy as np
import matplotlib.pyplot as plt
from lab_utils_multi import zscore_normalize_features, run_gradient_descent_feng
np.set_printoptions(precision=2)
-
from lab_utils_multi import zscore_normalize_features, run_gradient_descent_feng从自定义模块
lab_utils_multi中导入两个函数,zscore_normalize_features和run_gradient_descent_feng。这些函数通常用于特征标准化和运行梯度下降算法。 -
np.set_printoptions(precision=2)设置NumPy数组的打印选项,使得数组显示时的小数精度为两位。这在数据处理和调试时非常有用,因为它可以让输出更简洁,易于阅读。
特征工程和多项式回归概述
开箱即用的线性回归提供了一种构建以下形式模型的方法:
f w , b = w 0 x 0 + w 1 x 1 + … + w n − 1 x n − 1 + b (1) f_{\mathbf{w},b} = w_0x_0 + w_1x_1+ \ldots + w_{n-1}x_{n-1} + b \tag{1} fw,b=w0x0+w1x1+…+wn−1xn−1+b(1)
如果你的特征/数据是非线性的或是特征的组合怎么办?例如,房价往往不会随居住面积线性变化,但会对非常小或非常大的房屋进行惩罚,导致如上图所示的曲线。我们如何使用线性回归的工具来拟合这条曲线?回顾一下,我们所拥有的“工具”是修改(1)中的参数 w \mathbf{w} w 和 b \mathbf{b} b 以将方程“拟合”到训练数据。然而,仅通过调整(1)中的 w \mathbf{w} w 和 b \mathbf{b} b 是无法实现对非线性曲线的拟合的。
多项式特征
上面我们考虑了数据非线性的情况。让我们尝试使用我们目前所知道的方法来拟合一条非线性曲线。我们将从一个简单的二次方程开始: y = 1 + x 2 y = 1+x^2 y=1+x2
你已经熟悉我们使用的所有程序。它们在 lab_utils.py 文件中可以查看。我们将使用 np.c_[..],这是一个 NumPy 例程,用于沿列边界连接。
## 创建了目标数据
x = np.arange(0, 20, 1) # 生成一个从0到19的整数数组
y = 1 + x**2 # 定义了一个二次方程。实际值
X = x.reshape(-1, 1)
## 使用导入的梯度下降函数来拟合一个模型
model_w,model_b = run_gradient_descent_feng(X,y,iterations=1000, alpha = 1e-2)
## 绘制实际值和预测值的对比图
# 使用红色'x'标记绘制实际值。
plt.scatter(x, y, marker='x', c='r', label="Actual Value")
# 设置图表标题
plt.title("no feature engineering")
# 绘制预测值。X @ model_w + model_b 计算每个x的预测值。
plt.plot(x, X @ model_w + model_b, label="Predicted Value")
plt.xlabel("X") # 设置x轴标签
plt.ylabel("y")
plt.legend() # 显示图例
plt.show() # 显示图表
-
X = x.reshape(-1, 1)这一行代码将一维数组
x转换为二维数组X,这里的-1和1分别表示行数和列数。具体解释如下:reshape方法:reshape方法用于改变数组的形状,而不改变其数据。- 参数
-1:在reshape中,参数-1表示根据另一个维度自动计算这个维度的大小。在这个例子中,-1表示行数,由于我们指定了列数为1,reshape会根据x的长度自动计算出行数。 - 参数
1:表示列数为1。
这样做的目的是为了将数据转换成符合线性回归算法输入要求的格式,即每个样本是一行,每个特征是一列。在这个例子中,每个样本有一个特征,所以每行有一个元素。
-
plt.plot(x, X @ model_w + model_b, label="Predicted Value")-
x:这是原始的自变量数组,用于x轴。 -
X @ model_w + model_b:X是形状为(20, 1)的二维数组,每行一个特征。model_w是通过梯度下降算法得到的权重,它是一个数组或标量。model_b是通过梯度下降算法得到的偏置,它是一个标量。
具体计算过程:
X @ model_w:这一步是矩阵乘法。假设X的形状是(20, 1),model_w是(1, 1)(如果是标量,它会被自动广播)。结果是一个形状为(20, 1)的数组,每个元素是X中的值乘以model_w。- 其实就是实现了线性模型,获得了预测值
-
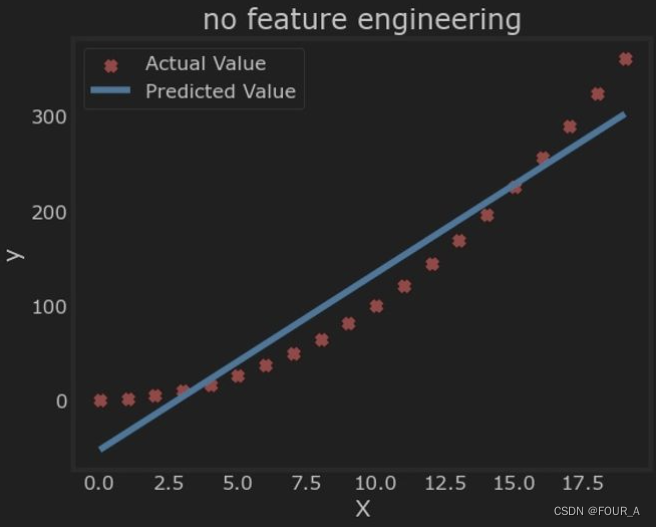
正如预期的那样,效果并不好。我们需要的是类似多项式特征的东西。为此,你可以**修改输入数据以构造所需的特征。如果你将原始数据替换为平方后的版本,那么你可以实现对非线性曲线的拟合。让我们试试看。将下面的 X 替换为 X2。
# create target data
x = np.arange(0, 20, 1)
y = 1 + x**2
# Engineer features
X = x**2 #<-- added engineered feature
X = X.reshape(-1, 1) #X should be a 2-D Matrix
model_w,model_b = run_gradient_descent_feng(X, y, iterations=10000, alpha = 1e-5)
plt.scatter(x, y, marker='x', c='r', label="Actual Value")
plt.title("Added x**2 feature")
plt.plot(x, np.dot(X, model_w) + model_b, label="Predicted Value")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()
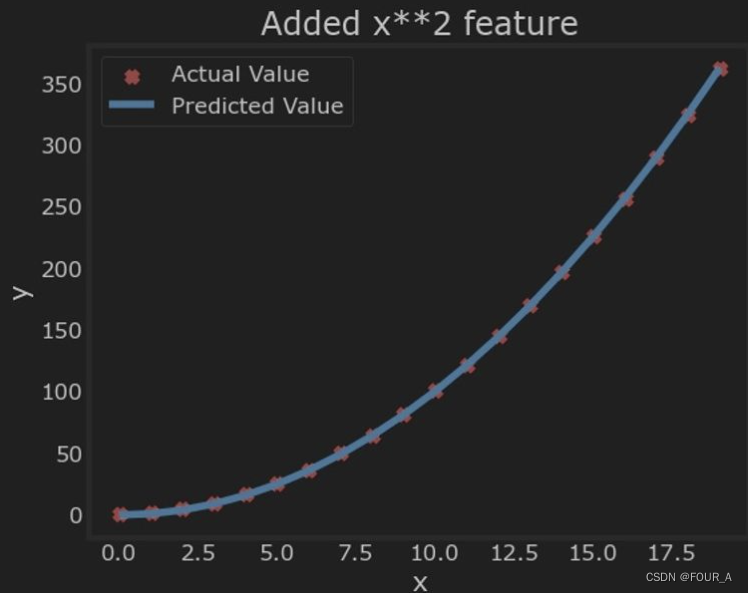
太棒了,几乎完美的拟合。请注意图表上方打印的 w w w 和 b b b 的值:通过梯度下降找到的 w , b w, b w,b 值为: w : [ 1.0 ] w: [1.0] w:[1.0], b : 0.0490 b: 0.0490 b:0.0490。梯度下降将我们的初始值修改为 ( 1.0 , 0.049 ) (1.0, 0.049) (1.0,0.049),即模型为 1.0 ∗ X 2 + 0.049 1.0*X^2 + 0.049 1.0∗X2+0.049,非常接近我们目标的 1 + X 2 1 + X^2 1+X2。如果运行时间更长,可能会得到更好的匹配。
选择特征
上面,我们知道需要一个 x 2 x^2 x2 项。但并不总是显而易见需要哪些特征。可以添加各种潜在特征来尝试找到最有用的。例如,如果我们尝试 y = w 0 x 0 + w 1 x 1 2 + w 2 x 2 3 + b y=w_0x_0 + w_1x_1^2 + w_2x_2^3+b y=w0x0+w1x12+w2x23+b 呢?
运行下一个单元格。
# create target data
x = np.arange(0, 20, 1)
y = x**2
# engineer features .
X = np.c_[x, x**2, x**3] #<-- added engineered feature
model_w,model_b = run_gradient_descent_feng(X, y, iterations=10000, alpha=1e-7)
plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("x, x**2, x**3 features")
plt.plot(x, X@model_w + model_b, label="Predicted Value"); plt.xlabel("x"); plt.ylabel("y"); plt.legend(); plt.show()
X = np.c_[x, x**2, x**3]-
使用
numpy的c_(column stack)函数将三个数组按列堆叠起来生成新的二维数组X。这里,x、x**2和x**3分别表示原始变量、变量的平方和变量的立方。 -
结果
X是一个二维数组,每行包含三个特征:x、x的平方和x的立方。例如:[ [0, 0, 0], [1, 1, 1], [2, 4, 8], [3, 9, 27], ... [19, 361, 6859] ]
-
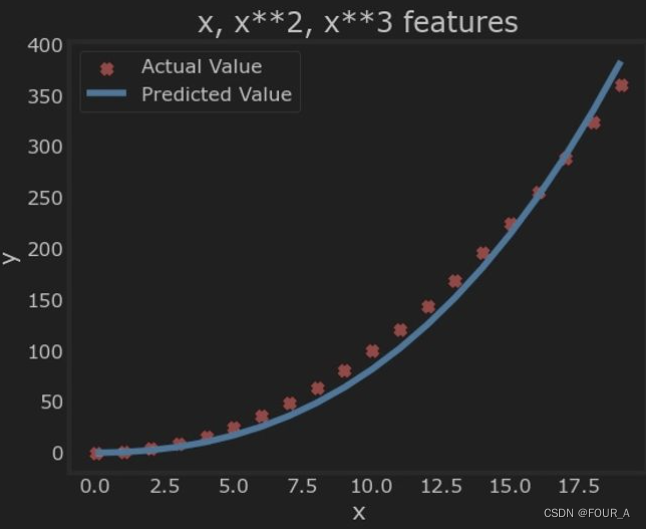
请注意
w
\mathbf{w}
w 的值为 [0.08, 0.54, 0.03],而
b
b
b 为 0.0106。这意味着模型在拟合/训练后的形式为:
0.08
x
+
0.54
x
2
+
0.03
x
3
+
0.0106
0.08x + 0.54x^2 + 0.03x^3 + 0.0106
0.08x+0.54x2+0.03x3+0.0106
梯度下降通过相对于其他项增加
w
1
w_1
w1 项,强调了与
x
2
x^2
x2 数据最匹配的数据。如果运行时间很长,它将继续减少其他项的影响。
梯度下降通过强调其相关参数,为我们选择了“正确”的特征。
让我们回顾这个想法:
- 最初,特征被重新缩放,使它们可以相互比较
- 较小的权重值意味着特征不太重要/正确,在极端情况下,当权重变为零或非常接近零时,相关特征对将模型拟合到数据中没有帮助
- 上面,在拟合后,与 x 2 x^2 x2 特征相关的权重比 x x x 或 x 3 x^3 x3 的权重大得多,因为它在拟合数据时最有用。
另一种观点
上面,多项式特征的选择基于它们与目标数据的匹配程度。另一种考虑方式是注意到,一旦我们创建了新的特征,我们仍在使用线性回归。鉴于此,最好的特征将相对于目标是线性的。通过一个例子来理解这一点是最好的。
# create target data
x = np.arange(0, 20, 1)
y = x**2
# engineer features .
X = np.c_[x, x**2, x**3] #<-- added engineered feature
X_features = ['x','x^2','x^3']
fig,ax=plt.subplots(1, 3, figsize=(12, 3), sharey=True)
for i in range(len(ax)): # 循环遍历每个子图
ax[i].scatter(X[:,i],y) # 在第i个子图上绘制散点图,X[:, i]表示第i列特征,y是目标变量
ax[i].set_xlabel(X_features[i]) # 设置第i个子图的x轴标签为对应的特征名称
ax[0].set_ylabel("y") # 设置第一个子图的y轴标签为"y"
plt.show()
-
X_features = ['x', 'x^2', 'x^3']创建一个列表**
X_features**,包含特征的名称。这对于理解和记录数据集中的特征非常有用,特别是在可视化和报告结果时。 -
fig, ax = plt.subplots(1, 3, figsize=(12, 3), sharey=True)- 使用**
matplotlib的subplots函数创建一个包含1行3列子图的图形对象。figsize=(12, 3)**设置图形的大小为12英寸宽,3英寸高。 - **
sharey=True**表示所有子图共享相同的y轴刻度。
- 使用**
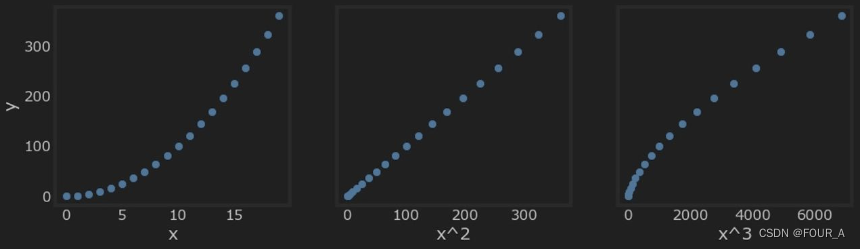
上面很明显,与目标值 y y y 相比, x 2 x^2 x2 特征是线性的。线性回归可以很容易地使用该特征生成模型。
特征缩放
如上一个实验中所述,如果数据集的特征具有显著不同的尺度,应应用特征缩放来加速梯度下降。在上面的例子中,有 x x x、 x 2 x^2 x2 和 x 3 x^3 x3,它们的尺度自然会有很大差异。让我们对我们的例子应用 Z-score 标准化。
# create target data
x = np.arange(0, 20, 1)
X = np.c_[x, x**2, x**3]
## 计算原始数据的峰值范围
print(f"Peak to Peak range by column in Raw X:{np.ptp(X, axis=0)}")
# 均值标准化
X = zscore_normalize_features(X)
# 计算标准化后的数据的峰值范围
print(f"Peak to Peak range by column in Normalized X:{np.ptp(X, axis=0)}")
## print
Peak to Peak range by column in Raw X:[ 19 361 6859]
Peak to Peak range by column in Normalized X:[3.3 3.18 3.28]
np.ptp(X, axis=0)ptp函数计算沿指定轴的峰值范围,即最大值和最小值之间的差值。axis=0表示按列计算。- 打印每列的峰值范围。
X = zscore_normalize_features(X)- 调用导入的
zscore_normalize_features函数对数据X进行 z-score 标准化。标准化后的每个特征将具有均值0和标准差1。
- 调用导入的
现在我们可以使用更激进的 alpha 值再次尝试:
x = np.arange(0,20,1)
y = x**2
X = np.c_[x, x**2, x**3]
X = zscore_normalize_features(X)
model_w, model_b = run_gradient_descent_feng(X, y, iterations=100000, alpha=1e-1)
plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("Normalized x x**2, x**3 feature")
plt.plot(x,X@model_w + model_b, label="Predicted Value"); plt.xlabel("x"); plt.ylabel("y"); plt.legend(); plt.show()
## print
w,b found by gradient descent: w: [5.27e-05 1.13e+02 8.43e-05], b: 123.5000
plt.plot(x, X @ model_w + model_b, label="Predicted Value")- 绘制预测值曲线。
X @ model_w + model_b表示用模型的权重和偏置计算每个**X**的预测值。
- 绘制预测值曲线。
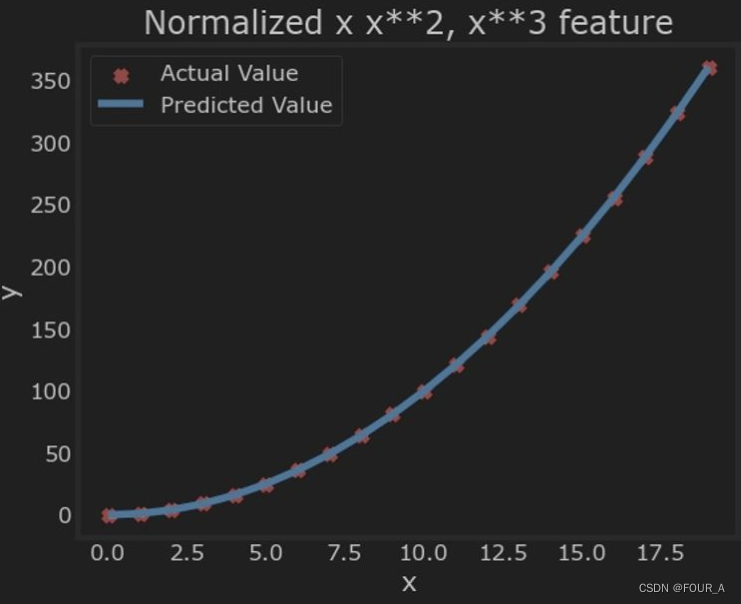
特征缩放使其收敛速度更快。
请再次注意 w \mathbf{w} w 的值。 w 1 w_1 w1 项,也就是 x 2 x^2 x2 项,最为突出。梯度下降几乎消除了 x 3 x^3 x3 项。
复杂函数
通过特征工程,即使是相当复杂的函数也可以建模:
x = np.arange(0,20,1)
y = np.cos(x/2) # 计算目标变量y,其值为x/2的余弦值。np.cos表示numpy的余弦函数。
X = np.c_[x, x**2, x**3,x**4, x**5, x**6, x**7, x**8, x**9, x**10, x**11, x**12, x**13]
X = zscore_normalize_features(X)
model_w,model_b = run_gradient_descent_feng(X, y, iterations=1000000, alpha = 1e-1)
plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("Normalized x x**2, x**3 feature")
plt.plot(x,X @ model_w + model_b, label="Predicted Value"); plt.xlabel("x"); plt.ylabel("y"); plt.legend(); plt.show()
## print
w,b found by gradient descent: w: [ -1.34 -10. 24.78 5.96 -12.49 -16.26 -9.51 0.59 8.7 11.94
9.27 0.79 -12.82], b: -0.0073
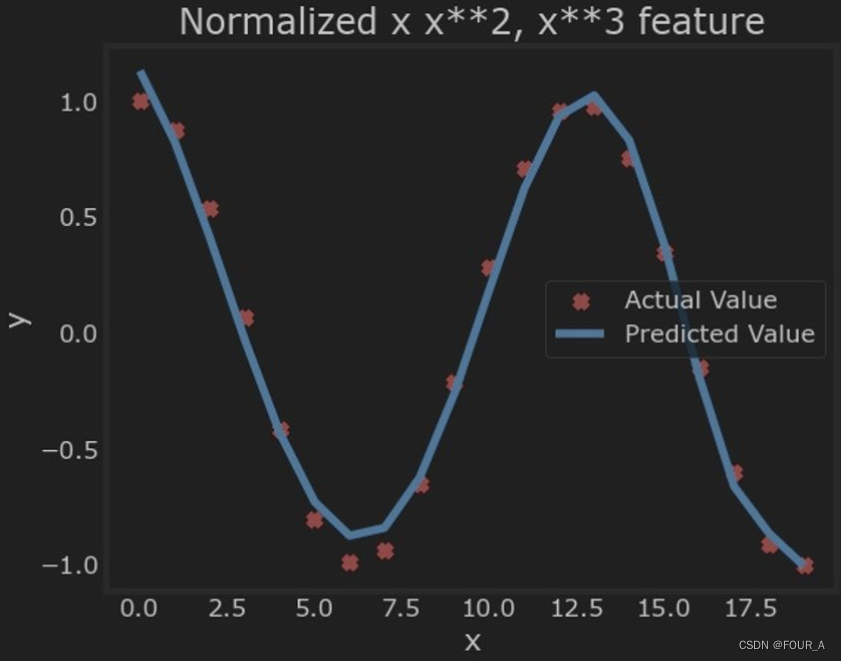
小结
- 学习了如何使用特征工程,通过线性回归建模复杂的,甚至是高度非线性的函数
- 认识到在进行特征工程时,应用特征缩放是很重要的