1.定义
所谓BRDF(Bidirectional Reflectance Distribution Function,双向反射分布函数),指的是从辐射度量学的角度去理解光线的反射,如下图所示。

所谓反射就是一个点从ωi方向发出的Radiance转化为dA接收到的功率E,然后功率E将转换为其他任何方向ωr发出的Radiance。 也就是一个点(微分面积元)在接受到一定方向上的亮度dE(ωi)之后,再向不同方向把能量辐射出去dLr(ωr)。
因此所谓BRDF就是描述这样一个光线从不同方向入射之后,反射光线的分布情况的函数。数学定义如下。

上图中下方的式子即为BRDF,它接收两个参数,入射光方向ωi,反射光方向ωr,函数值为反射光的radiance与入射光的iiradiance的比值(从某个方向接受到的光能有多少反射到另外一个方向)。
从直观的理解来说,不同材质的表面自然会把一定方向上的入射光线反射到不同方向上,如理想光滑表面会把入射光线完全反射到镜面反射方向,其它方向则完全没有。而理想粗糙表面会把入射光线均匀的反射到所有方向。
2.性质
1.BRDF是非负的(Non-negativity),表示了能量的分布。
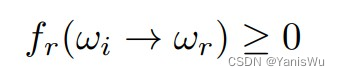
2.BRDF是线性的(Linearity),可以拆分和叠加。

3.BRDF是可逆的(Reciprocity principle),调换入射方向和出射方向依然成立。
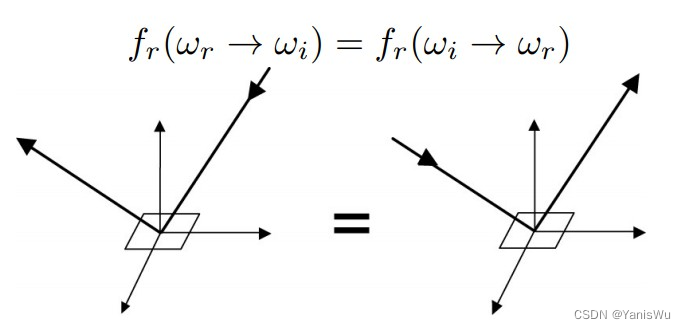
4.BRDF满足能量守恒(Energy conservation),入射能量等于反射能量(存在能量吸收的情况时,入射能量大于反射能量)。
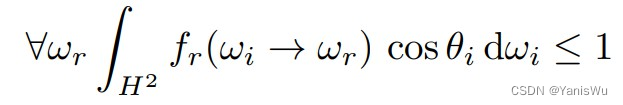
3.反射方程
借助BRDF,可以定义出反射方程如下。
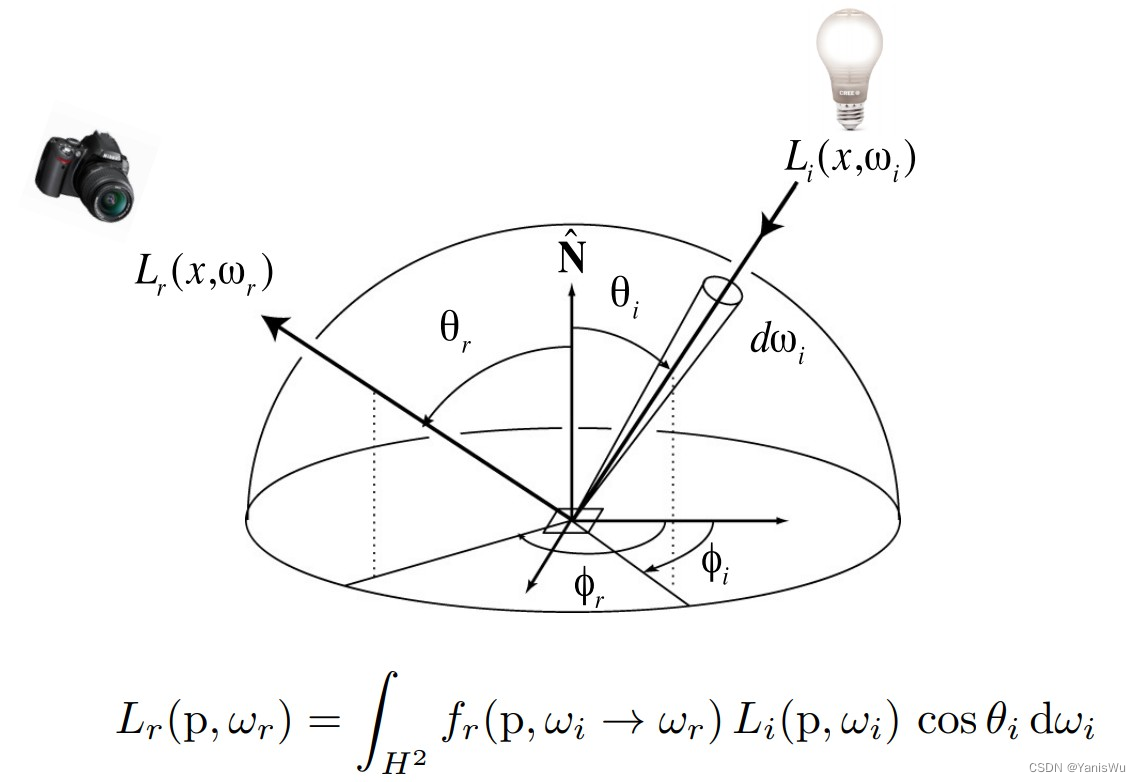
因为BRDF表示从某一个方向考虑入射,然后往某一个方向反射出去会是什么样的结果。假如以某一个反射方向ωr出去的点,从相机方向看到的这个着色点可以接收来至四面八方的不同的光照。那就考虑对于每一个入射方向ωi,都会对应入射方向着色点和出射方向这样的BRDF。BRDF会告诉我们从某一个方向进来的光反射到出射方向有多强,那就将每个方向的入射光线的强度(Radiance)乘以BRDF,再乘以(之前的定义),然后把每一个方向上对出射光线的贡献相加,这样就得到了这个点在所有可能得入射光下反射到ωr上的情况。
如上可知,所谓的反射方程定义了任何一个着色点在各个不同的光照环境下,考虑任何一个光照入射方向对观察方向(出射方向)的一个贡献,将所有入射方向的贡献相加,相加就是求一个积分,得到最终的着色效果。
在进入到渲染方程之前,再仔细观察一下反射方程。
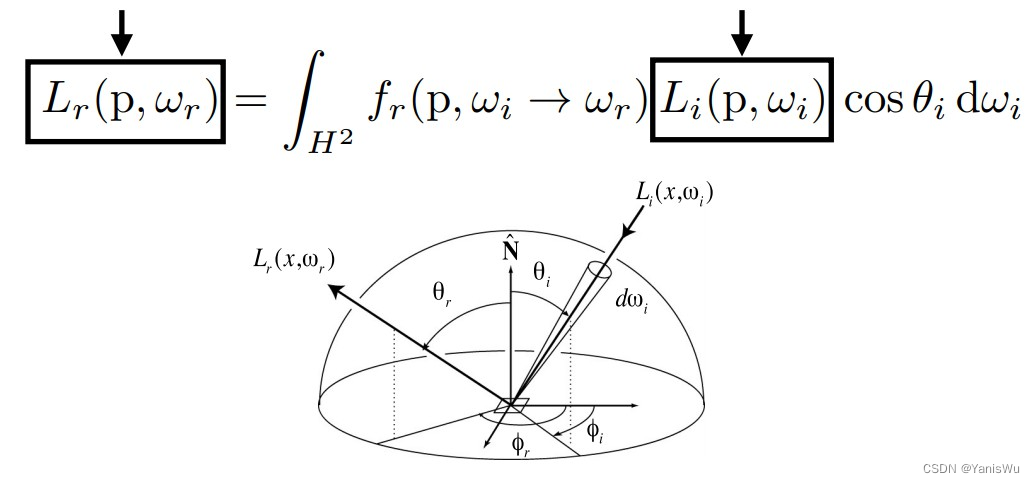
假如从某个方向观察某个着色点,要考虑所有能够到达这个着色点的所有光线,但是能够达到的可不止是光源发出的光线,还有可能有其他物体上着色点反射的光线,即间接光照。也就是说考虑的入射radiance不止来至光源,也可能来至其他物体反射出去的radiance,这是一个递归的过程。即任何出射的radiance都可能是其他入射的radiance,这就是为什么光线在场景中不止弹射一次的原因,这是一个很难计算的问题。
4.渲染方程
4.1 定义
渲染方程只是在反射方程的基础之上添加了一个自发光项(Emission term),用来模拟物体自发光(物体有自发光和反射光),从而使得反射方程更加的通用,适用于所有物体表面上的光线传播问题。如下公式。
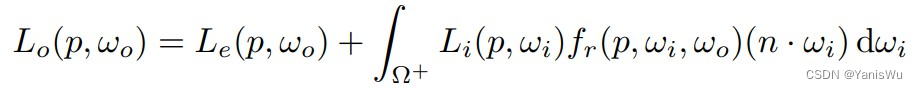
其中Le(p,ω0)为自发光项,反射方程中的 cosθ 用 n·ωi 代替 (一样)。注意:所有光线方向均以从平面向外为正方向。
4.2 理解渲染方程
1.一个点光源和单个物体的场景

点光源对一个点来说自然只有一个方向有入射光,所以这里没有了积分(相加)。
2.多个点光源一个物体的场景
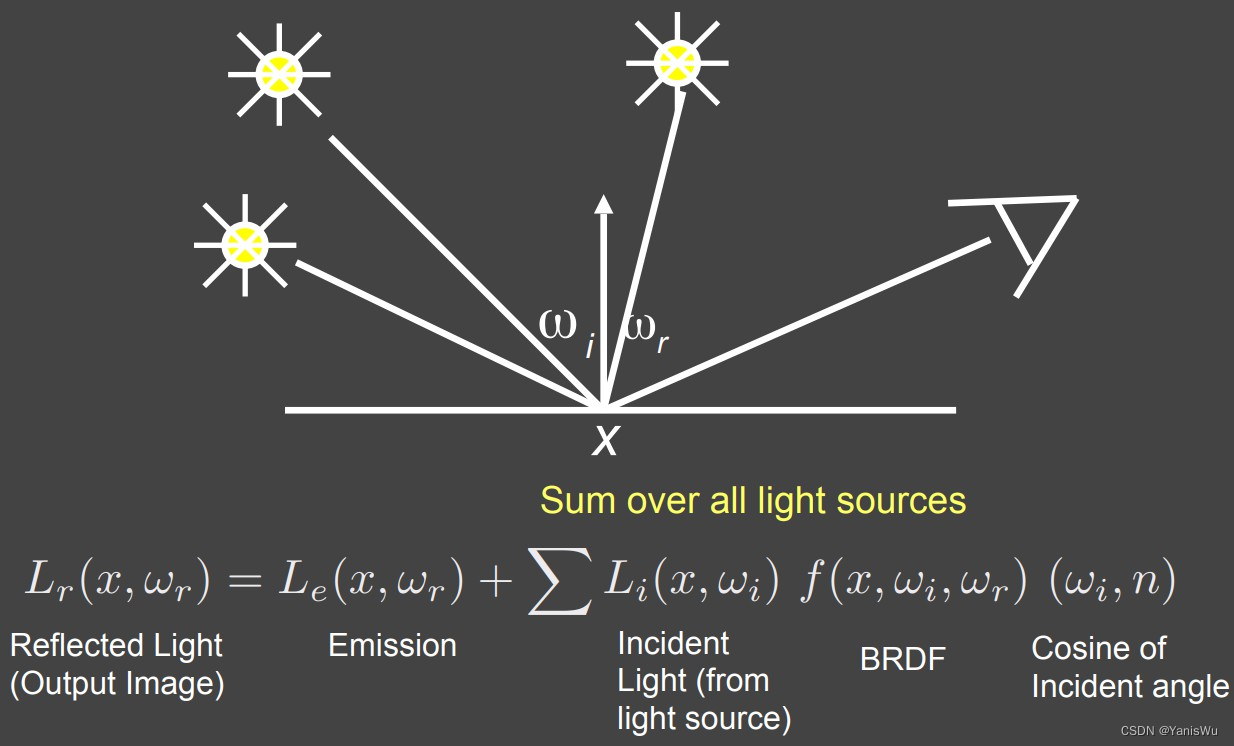
将所有的点光源的贡献全部求和即可。
3.那么如果有一个是面光源呢?

其实面光源就相当于无穷多个点光源的集合,由于多个点光源贡献可以相加,那么对面光源任意一点的贡献积分(相加)道理是一样,所以对这个面占据的立体角范围进行积分,然后考虑所有的方向Radiance经过BRDF反射出去的样子。
4.在场景当中加入其它物体,使得物体之间发生光线交互之后是什么情况呢?
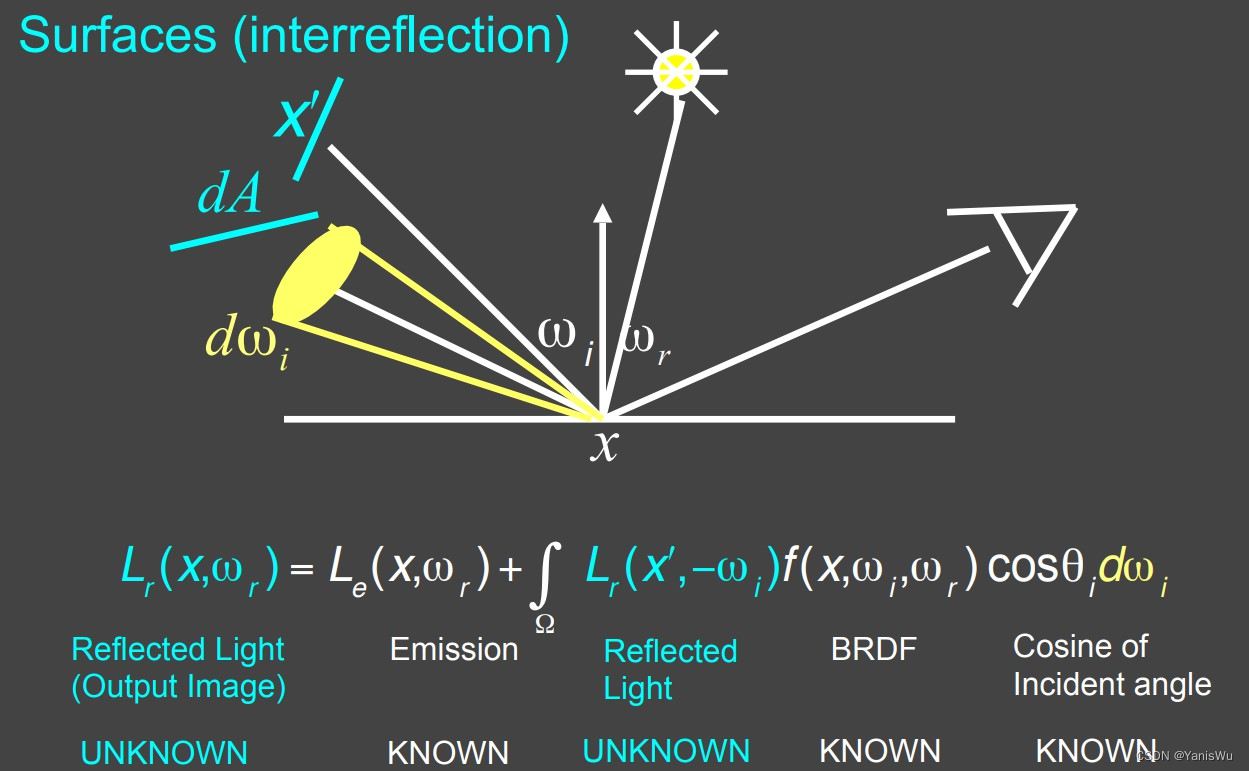
可以把其它物体同样考虑成面光源,对其所占立体角进行积分即可,只不过对其它物体的立体角积分不像是面光源所有入射方向都有radiance,物体的立体角可能只有个别几个方向有入射的radiance(即多次物体间光线反射之后恰好照射到着色点x),其它方向没有,但本质上都可以视作是面光源。
图中的渲染方程除了两个radiance,其它所有项都是知道的,可以将上式进一步写成如下图下方所示的简单式子。

其中各项与原渲染方程中一一对应,(这里其实是有数学严格推导的,不过我们只是为了接下来构建直观的物理解释,对于这些推导不必在意,默认成立即可),再接着,可以把该式子离散化写为线性代数的形式。

经过两步我们不是很清楚但其实是正确的数学推导之后,得到了这样一个递归式。
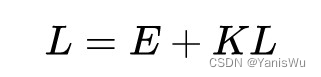
其中L其实就是想要求得的反射光,E是自发光其实就是光源的发光项,K可以理解为对光线进行反射的一种算子操作(因为它由BRDF转化来的)。
那么利用线性代数的知识很容易就可以推导出L的结果如下。
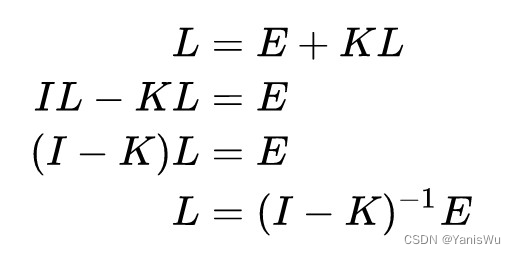
其中 I 为单位矩阵,再接着使用广义二项式定理得到。
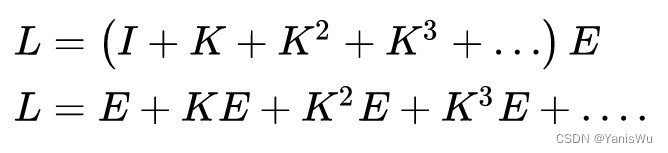
仔细观察这个式子,注意E是光源所发出的光,K为反射算子,这样一个式子的物理含义如下图所示。
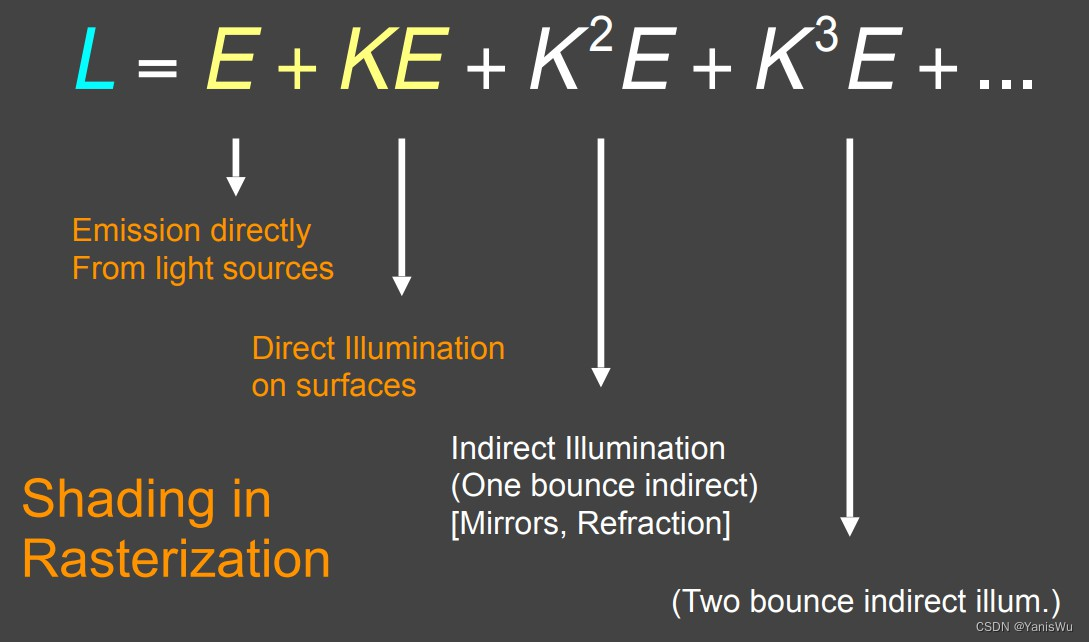
E为光源发出的光,KE则代表对光源反射一次的结果,即直接光照,那么前两项之和就是光栅化当中着色所考虑的结果。对于全局光照(所有光线弹射次数加起来)来说,还考虑了第三项,即一次弹射的间接照明,
就是两次弹射的间接照明,依次类推。
这样来看整个结果就很清晰了,就是光源发光加上直接光照与多次间接光照的结果!而这一切都是从渲染方程推导而来的,因此这也正是渲染方程的物理意义!
不同弹射次数下同一场景的渲染效果如下。

显然弹射次数越多越接近真实图片效果,但提升幅度逐渐递减。
注意:图片顶部中间有块玻璃,当进行第4次弹射时才从黑色变亮。这是因为光从相机出来到玻璃球里至少弹射2次才能出来,如果玻璃是双层的2次弹射只能进去,再经过2次弹射才能出来。