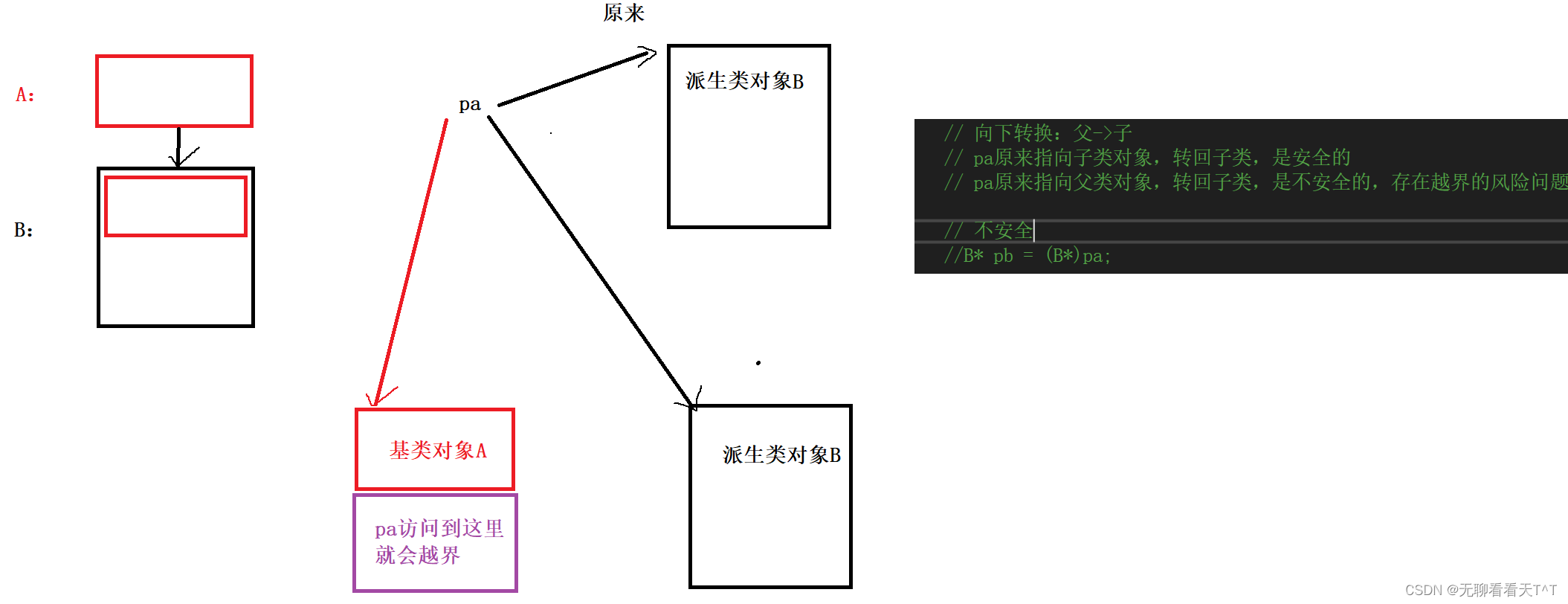
3197. 包含所有 1 的最小矩形面积 II
题目描述:
给你一个二维 二进制 数组 grid。你需要找到 3 个 不重叠、面积 非零 、边在水平方向和竖直方向上的矩形,并且满足 grid 中所有的 1 都在这些矩形的内部。
返回这些矩形面积之和的 最小 可能值。
注意,这些矩形可以相接。
1 < = g r i d . l e n g t h , g r i d [ i ] . l e n g t h < = 30 1 <= grid.length, grid[i].length <= 30 1<=grid.length,grid[i].length<=30
思路:
观察数据范围,n只有30,估计是 O ( n 4 ) O(n^4) O(n4)甚至是 O ( n 5 ) O(n^5) O(n5),所以要想办法暴力
我们只能做到 O ( n 2 ) O(n^2) O(n2)的方法去计算一个区域中用一个矩形覆盖的情况
所以要想办法只枚举两次就能把图形分割成三份,情况如下
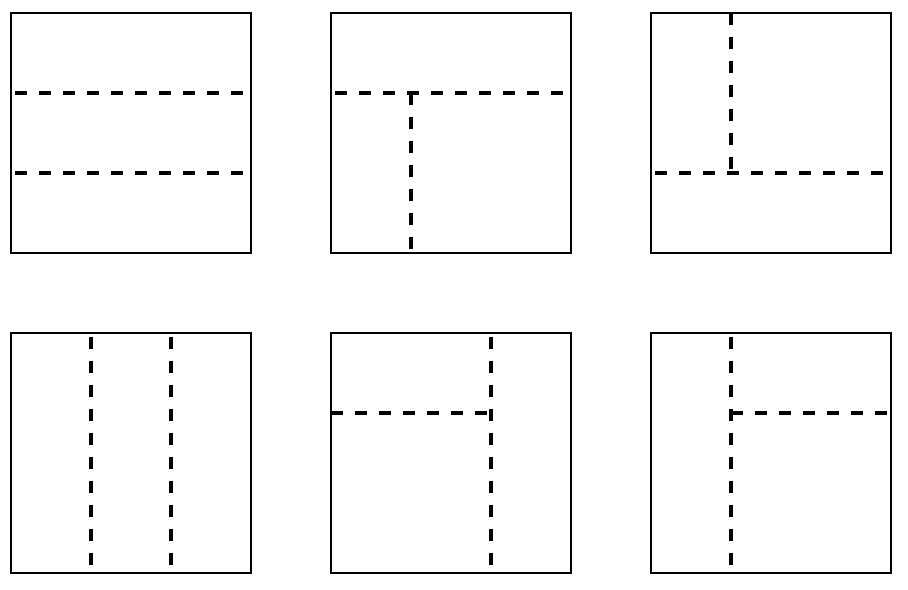
写代码的时候要仔细,注意下标
class Solution {
public:
int n, m, tr[35][35];
int cal(int x1, int y1, int x2, int y2){
bool fuck = 0;
int x_max = 0, x_min = 1e9, y_max = 0, y_min = 1e9;
for(int i = x1; i <= x2; ++i){
for(int j = y1; j <= y2; ++j){
if(tr[i][j]){
fuck = 1;
x_max = max(x_max, i);
x_min = min(x_min, i);
y_max = max(y_max, j);
y_min = min(y_min, j);
}
}
}
if(fuck == 0)return 0;
return (x_max - x_min + 1) * (y_max - y_min + 1);
}
int minimumSum(vector<vector<int>>& num) {
n = num.size();
m = num[0].size();
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j){
tr[i][j] = num[i - 1][j - 1];
}
}
int ans = 1e9;
for(int i = 1; i <= n; ++i){
for(int j = i + 1; j <= n; ++j){
ans = min(ans, cal(1,1, i, m) + cal(i + 1, 1, j, m) + cal(j + 1, 1, n, m));
}
for(int j = 1; j <= m; ++j){
ans = min(ans, cal(1, 1, i, j) + cal(i + 1, 1, n, j) + cal(1, j + 1, n, m));
ans = min(ans, cal(1, 1, n, j) + cal(1, j + 1, i, m) + cal(i + 1, j + 1, n, m));
ans = min(ans, cal(1, 1, i, j) + cal(1, j + 1, i, m) + cal(i + 1, 1, n, m));
ans = min(ans, cal(1, 1, i, m) + cal(i + 1, 1, n, j) + cal(i + 1, j + 1, n, m));
}
}
for(int i = 1; i <= m; ++i){
for(int j = i + 1; j <= m; ++j){
ans = min(ans, cal(1, 1, n, i) + cal(1, i + 1, n, j) + cal(1, j + 1, n, m));
}
}
return ans;
}
};