一、代码理解
目的:设计思路(根据)
【主程序】多进程,linux,tensorflow
随机生成速度模型的显示颜色,位置,大小
训练的多进程安排
创建目录、环境变量,来存储CMP地震数据
定义变量,来控制程序的生成和训练
先是生成速度模型->正演数据集
建立网络(在jupyter notebook)->训练网络->测试网络
【CNN】
1.利用 Seismic Unix(SU)工具集。将模型分解为CMP(Common Mid-Point)集合,并进行可视化。——没明白怎么分解的
# sort into cmp gathers and discard odd cmps
print(f"sfshot2cmp < shots_decimated.rsf half=n | sfwindow j3=2 min3={(-gxbeg+2*sxbeg)*dx} max3={(Nx-(2*sxbeg))*dx} > {shots_out}")
cmd(f"sfshot2cmp < shots_decimated.rsf half=n | sfwindow j3=2 min3={(-1.5*gxbeg+1.5*sxbeg)*dx} max3={(Nx-(2.5*sxbeg-.5*gxbeg))*dx} > {shots_out}")
2.将地震数据转化成多个CMP输入(10炮)——没明白怎么转化的
# expand to multiple CMPs as channels in input
def make_multi_CMP_inputs(X_data, T_data, nCMP, n_models=1):
# first we prepare array for X_data_multi_CMP
X_data_multi_CMP = np.zeros((n_models,
X_data.shape[0]//n_models-nCMP+1,
X_data.shape[1],
X_data.shape[2],
nCMP))//5D 数据
# add model dimension
X_data = X_data.reshape(n_models, X_data.shape[0]//n_models, X_data.shape[1], X_data.shape[2], 1)
T_data = T_data.reshape(n_models, T_data.shape[0]//n_models, T_data.shape[1])
for i in range(nCMP-1):
print(i)
#print(np.shape(X_data_multi_CMP))
#print(np.shape(X_data))
#print(nCMP)
#print(-nCMP+i+1)
X_data_multi_CMP[:,:,:,:,i] = X_data[:,i:-nCMP+i+1,:,:,0]//对原始地震数据做处理得到多通道的CMPs
X_data_multi_CMP[:,:,:,:,nCMP-1] = X_data[:,nCMP-1:,:,:,0]
if nCMP==1 :
T_data_multi_CMP = T_data
else :
T_data_multi_CMP = T_data[:, (nCMP-1)//2 : -(nCMP-1)//2, :]
X_data_multi_CMP = X_data_multi_CMP.reshape(X_data_multi_CMP.shape[0]*X_data_multi_CMP.shape[1],
X_data_multi_CMP.shape[2],
X_data_multi_CMP.shape[3],
X_data_multi_CMP.shape[4])
T_data_multi_CMP = T_data_multi_CMP.reshape(T_data_multi_CMP.shape[0]*T_data_multi_CMP.shape[1],
T_data_multi_CMP.shape[2])
#print(-(nCMP+1)//2) print(np.shape(X_data_multi_CMP)) print(np.shape(T_data_multi_CMP))
assert (X_data_multi_CMP.shape[0] == T_data_multi_CMP.shape[0])
return X_data_multi_CMP, T_data_multi_CMP
nCMP = 1
X_scaled, T_scaled = make_multi_CMP_inputs(X_scaled, T_scaled, nCMP, n_models=random_model_repeat)
nCMP = 11
X_scaled_multi, T_scaled_multi = make_multi_CMP_inputs(X_scaled, T_scaled, nCMP, n_models=random_model_repeat)
plt_nb_T(T_data, dx=jgx*dx, dz=jlogz*dx, fname="../latex/Fig/T_data")
plt_nb_T(1e3*T_scaled, dx=jgx*dx, dz=jlogz*dx, fname="../latex/Fig/T_scaled")
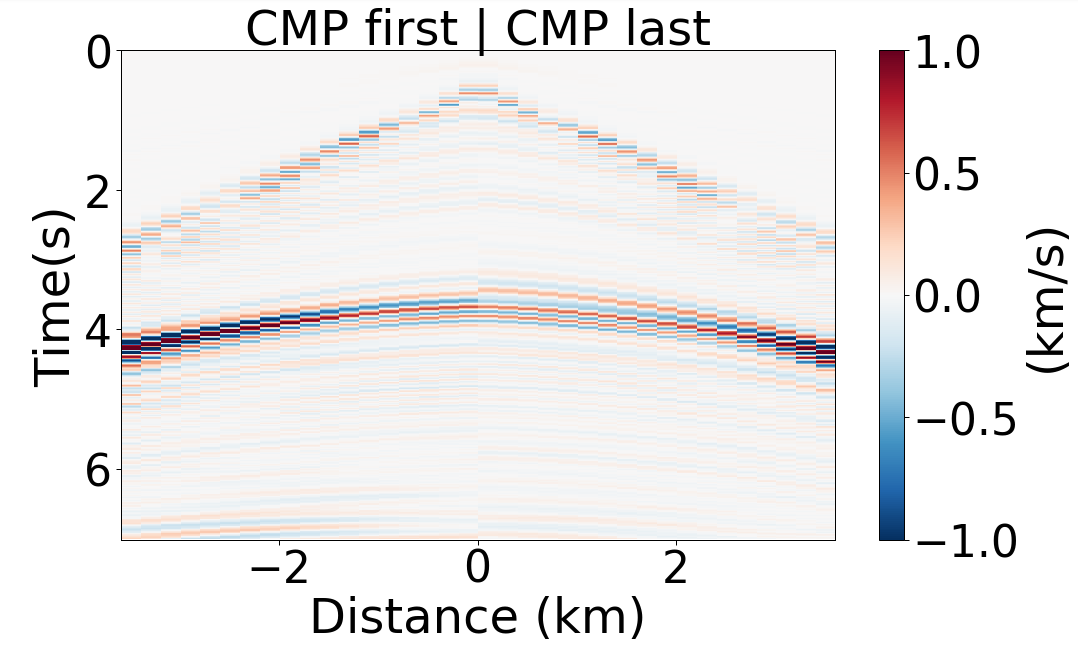
3.地震数据的拼接(经过翻转再拼接)——但不理解为什么只要第一个和最后一个的拼接
plt_nb_T(1e3*np.concatenate((np.squeeze(X_scaled[sample_reveal-nCMP,:,:,-1]), np.flipud(np.squeeze(X_scaled[sample_reveal,:,:,0]))), axis=0),
title="CMP first | CMP last", dx=200, dz=1e3*dt*jdt,
origin_in_middle=True, ylabel="Time(s)", fname="../latex/Fig/X_scaled")
print(np.shape(1e3*T_scaled[sample_reveal-(nCMP+1)//2:sample_reveal+(nCMP-1)//2:nCMP]))
使用 plt_nb_T 函数绘制了 X_scaled 数组中的特定样本。这个样本是将第 nCMP 个最后一个CMP的数据和第一个CMP的数据拼接在一起,然后放大1000倍(可能是为了清晰度,因为地震数据通常在很大的数量级上)。
np.squeeze(…):
使用 NumPy 的 squeeze 函数去除数组中的单维度条目(即去除大小为1的维度)
plt_nb_T(1e3*np.concatenate((np.squeeze(X_data_cut[sample_reveal-nCMP,:,:,-1]), np.flipud(np.squeeze(X_data_cut[sample_reveal,:,:,0]))), axis=0),
title="CMP first | CMP last", dx=200, dz=1e3*dt*jdt,
origin_in_middle=True, ylabel="Time(s)", fname="../latex/Fig/X_muted")
title=“CMP first | CMP last”:
设置图表的标题,表示图表展示了第一个和最后一个CMP的数据。
np.concatenate(…, axis=0):
使用 NumPy 的 concatenate 函数沿 axis=0 将两个数组拼接在一起。这里拼接的是特定样本的最后一个CMP和翻转后的(翻转使用 np.flipud)第一个CMP的数据。
dx=200, dz=1e3dtjdt:
设置图表的水平和垂直采样间隔。dt 和 jdt 可能是之前定义的时间步长和某个时间缩放因子。
origin_in_middle=True:
设置图像原点在中间,这通常用于对称的图形表示。
ylabel=“Time(s)”:
设置Y轴标签为“Time(s)”,表示Y轴的单位是秒。
fname="…/latex/Fig/X_scaled":
设置保存图像的文件名。
4.架构
def create_model(inp_shape, out_shape, jlogz=jlogz):
model = keras.models.Sequential()
activation = 'relu'
activation_dense = activation
padding = 'same'
dropout = 0.1
model.add(Conv2D(filters=4, kernel_size=(5, 21), strides=(2,5), activation=activation, padding=padding, input_shape=inp_shape))
model.add(Dropout(dropout))
model.add(Conv2D(filters=16, kernel_size=(7, 11), activation=activation, padding=padding))
model.add(MaxPool2D([1,2]))
model.add(Dropout(dropout))
model.add(Conv2D(filters=32, kernel_size=(3, 11), activation=activation, padding="valid"))
model.add(Dropout(dropout))
model.add(Conv2D(filters=32, kernel_size=(3, 7), activation=activation, padding=padding))
model.add(Dropout(dropout))
model.add(Conv2D(filters=32, kernel_size=(5, 5), activation=activation, padding=padding))
model.add(Dropout(dropout))
model.add(Conv2D(filters=1, kernel_size=(7, 60), strides=(10,jlogz//2), activation="linear", padding=padding))
model.add(Dropout(dropout))
model.add(Flatten())
#model.add(Dense(2*out_shape[0], activation=activation_dense))
#model.add(Dense(out_shape[0], activation=activation_dense))
#model.add(Dropout(0.1))
#model.add(Dense(out_shape[0], activation='linear'))
#model.add(Reshape(out_shape))
model.compile(loss='mse',
optimizer=keras.optimizers.Nadam(),
metrics=['accuracy'])
return model
二、问题
1.CNN得到的是频率,怎么生成的速度模型呢?好突然,
A:速度模型作为初始模型。经正演得到波形,频率指的是波形的高频、低频。
参考意义:生成数据的迭代阶段。凡是有速度模型,可以在此基础上去正演得到波形,利用波形的高频信息恢复/外推波形低频信息。由波形出发反演速度模型。
2.SimpleFWI中,波形和地震记录(raw data体现在哪)什么对应关系?
为什么作者反演的深度这么浅?
为什么从2-4Hz开始?这也不算高频呀?
3.Mapping中的
什么是“源中心频率为5Hz的全频段数据”?
4.不理解对第i个CMP处理在干嘛:X_data_multi_CMP[:,:,:,:,i] = X_data[:,i:-nCMP+i+1,:,:,0]?
输出X_data_multi_CMP为什么是这个样子?(10个CMP的原始数据)
三、已解答的问题
- Elastic Transform(弹性变换)是一种数据增强技术,特别适用于图像数据集的增强。它通过模拟图像的物理弹性变形来增加数据的多样性,有助于提高深度学习模型的泛化能力。以下是使用弹性变换进行数据增强的一些关键点:
-
原理:弹性变换通过在图像上应用随机生成的位移场来模拟弹性变形。位移场通常是通过高斯分布生成的随机向量,然后使用高斯滤波器进行平滑处理。
-
参数:弹性变换的两个关键参数是
alpha和sigma。alpha控制位移的大小,而sigma控制高斯滤波器的平滑程度。 -
应用:弹性变换可以应用于医学图像分析、手写识别、自然语言处理等领域,以增加数据集中样本的多样性。
-
实现:在Python中,可以使用像PyTorch这样的深度学习框架来实现弹性变换。例如,
torchvision.transforms模块提供了ElasticTransform类,可以轻松地将弹性变换应用到图像数据上。 -
效果:弹性变换能够模拟图像的复杂变形,包括拉伸、压缩和扭曲,这有助于模型学习到更加鲁棒的特征表示。
-
与其他数据增强技术的比较:与传统的旋转、翻转或裁剪等数据增强技术相比,弹性变换可以引入更复杂的图像变形,从而更有效地提高模型对图像变形的适应能力。
-
使用注意事项:在使用弹性变换时,需要仔细调整
alpha和sigma的值,以确保生成的图像既具有多样性,又不会失去重要的视觉信息。
通过使用弹性变换,可以有效地扩充图像数据集,提高模型对新情况的适应性,从而在各种视觉识别任务中取得更好的性能。——此弹性非彼弹性(不是弹性波,只是图像上的扰动)
- Mapping文献中,高斯随机场用于产生横向平滑模型的坐标偏移目的:
- 水平方向的大相关半径- -为保持其近乎水平层状
- 垂直方向上的小相关半径- -为使其代表不同的分层场景
- 水平分量和垂直分量的参数相同,但场不同
- 大的垂直位移和小的水平位移- -为保持其横向缓慢变化
下一步工作
1.了解Seismic Unix(SU)工具集。
2.把cmp输入数据的形式和处理目的理解清楚,把速度分析和地震反演两个问题的网络合理结合,目的是将其作为深度网络的输入数据。
需要理解的资料主要是有openfwi数据集所提到的3种网络。