💓 博客主页:倔强的石头的CSDN主页
📝Gitee主页:倔强的石头的gitee主页
⏩ 文章专栏:《数据结构与算法》
期待您的关注
目录
一、引言
二、堆的基本概念
🍃堆的特性
🍃堆的分类
三、数组与堆的关联
🍃为什么选择数组
🍃数组与堆的映射关系(重要)
四、堆的结构定义
五、堆的接口实现
🍃初始化
🍃销毁
🍃向上调整算法
🍃入堆
🍃向下调整算法
🍃出堆
🍃取堆顶元素
🍃对堆判空
🍃获取堆的数据个数
六、C语言实现堆的代码示例
🍃Heap.h //堆的头文件
🍃Heap.c //堆的源文件
🍃test.c //mian函数测试文件
🍃测试结果
七、性能分析
八、应用场景
九、总结
一、引言
堆是一种特殊的树形数据结构,其每个节点的值都大于或等于(大顶堆)或小于或等于(小顶堆)其子节点的值。在计算机科学中,堆常用于实现优先级队列、堆排序等算法。本文将探讨如何使用数组实现堆,并分析其原理、实现细节以及应用场景。
二、堆的基本概念
🍃堆的特性
- 堆是一棵完全二叉树,通常使用数组进行存储。
- 堆中任意节点的值都满足堆的性质,即大顶堆中父节点的值大于或等于其子节点的值,小顶堆中父节点的值小于或等于其子节点的值。
🍃堆的分类
- 大顶堆:父节点的值大于或等于其子节点的值。
- 小顶堆:父节点的值小于或等于其子节点的值。
三、数组与堆的关联
🍃为什么选择数组
- 数组在内存中是连续存储的,可以高效地进行访问和修改。
- 对于完全二叉树,可以使用数组进行简单的索引计算来访问任意节点。
注意:我们只是把数组在逻辑上想象成了抽象的堆,其实它本质上就是数组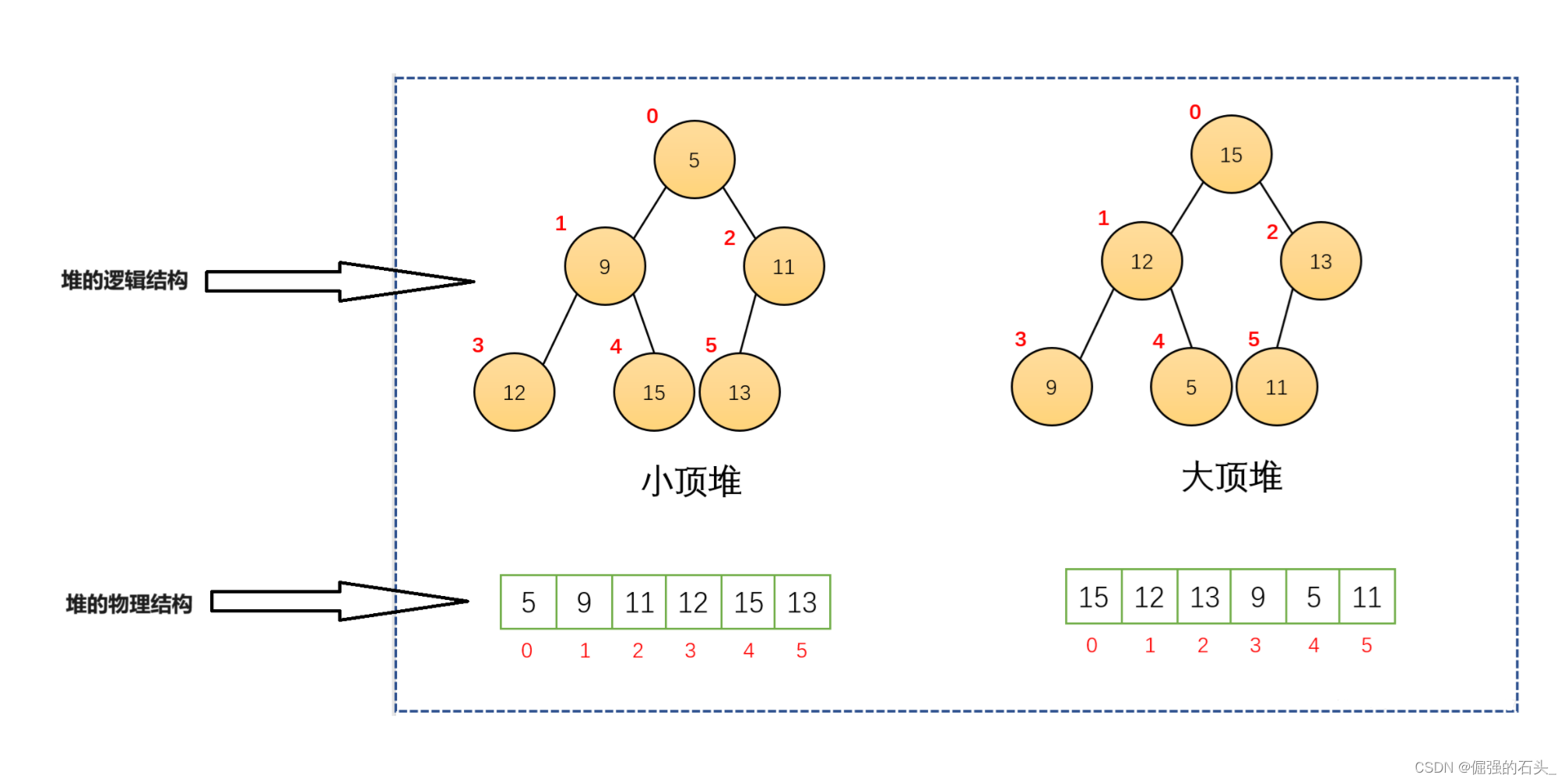
🍃数组与堆的映射关系(重要)
- 若某节点在数组中的下标为i(i从0开始),则其左子节点(若存在)的下标为2i+1,右子节点(若存在)的下标为2i+2,其父节点(若存在)的下标为(i-1)/2
- 堆的根节点在数组中的下标通常为0。
四、堆的结构定义
堆的结构定义与顺序表基本是一致的,这也更说明了堆的概念更多的是在逻辑上更加抽象
包括
- 指向某种数据类型的指针(用来实现数组)
- 数组的有效数据个数size
- 数组的空间大小capacity
typedef int HPDataType;//数据类型重定义
typedef struct Heap//堆的结构定义
{
HPDataType* a;
int size;
int capacity;
}Heap;
五、堆的接口实现
🍃初始化
- 首先对形参接收的地址判空
- 指针初始为NULL
- size和capacity初始为0
void HeapInit(Heap* php)//初始化
{
assert(php);
php->a = NULL;
php->size = php->capacity = 0;
}
🍃销毁
- 对形参接收的地址判空
- 释放为数组动态开辟的空间,并置为NULL
- size和capacity修改为0
void HeapDestory(Heap* hp)//销毁
{
assert(hp);
free(hp->a);
hp->a = NULL;
hp->size = hp->capacity = 0;
}
🍃向上调整算法(重要)
- (该函数在这里是为入堆准备的)
- 接收两个参数,分别是数组或指针,以及对应需要调整的节点位置
- 思想:从该位置向上调整,直到父子满足大小关系,或调整至根结点
void Adjustup(HPDataType* a, int child)//向上调整算法
{
assert(a);//数组必须存在,否则解引用就会报错
int parent = (child - 1) / 2;
while (child > 0 && a[parent] > a[child])//这里以小堆调整为例
{
Swap(&a[parent], &a[child]);//交换数据必须传地址
child = parent;
parent= (child - 1) / 2;
}
}这里额外封装了一个交换函数,方便后面多次使用,并且想要通过形参改变实参的值,需要传址调用
void Swap(HPDataType* a, HPDataType* b)//交换函数
{
HPDataType tmp = *a;
*a = *b;
*b = tmp;
}
🍃入堆
- 接收两个参数:数组或指针,以及要插入的数据
- 对形参接收的地址判空
- 判断数组有剩余空间(若不足,扩容)
- 将新数据插入到数组最后一个有效数据的后面
- 之后调用向上调整算法 重新调整为堆
void HeapPush(Heap* hp, HPDataType x)//入堆
{
assert(hp);//接收的堆地址必须是有效的
if (hp->size == hp->capacity)//判断是否需要扩容
{
int newcapacity = hp->capacity == 0 ? 4 : (hp->capacity) * 2;
HPDataType* tmp = (HPDataType*)realloc(hp->a,sizeof(HPDataType) * newcapacity);
if (tmp == NULL)
{
perror("Push perror\n");
exit(1);
}
hp->a = tmp;
hp->capacity = newcapacity;
}
hp->a[hp->size++] = x;//插入到尾部
Adjustup(hp->a, hp->size - 1);//进行向上调整
}
🍃向下调整算法(重要)
- 接收三个参数,数组或指针,以及parent对应要调整的位置,比向上调整算法额外多一个参数n(数组有效数据个数),用来判断是否调整到叶子结点
- 思想:以小堆为例,child等于parent两个孩子中较小的孩子,从该位置开始比较和调整,直到满足堆的大小关系或者调整到叶子结点
void Adjustdown(HPDataType* a, int parent, int n)//向下调整算法
{
assert(a);
int child = parent * 2 + 1;//先假设左孩子小
while (child < n)
{
if (child + 1 < n && a[child + 1] < a[child])//这里以小堆调整为例
child++;//如果右孩子存在,且右孩子小,父节点与右孩子进行比较
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
🍃出堆
- 接收一个参数:数组或指针,表示堆
- 首先对形参接收的地址判空
- 然后判断堆是否为空
- 交换堆顶和堆尾数据,size--
- 然后从堆顶开始进行向下调整
void HeapPop(Heap* hp)//出堆
{
assert(hp);
assert(hp->size);//判断堆不为空
Swap(&(hp->a[0]), &(hp->a[hp->size - 1]));
hp->size--;//第一个数据与最后一个数据交换,然后删除最后一个
Adjustdown(hp->a, 0, hp->size);
}
🍃取堆顶元素
- 对形参判空,并且堆不能为空
- 然后返回数组的第一个数据
HPDataType HeapTop(Heap* hp)// 取堆顶的数据
{
assert(hp);
assert(hp->size);
return hp->a[0];
}
🍃对堆判空
- 对形参判空
- 然后返回size==0的结果
int HeapEmpty(Heap* hp)//堆的判空
{
assert(hp);
return hp->size == 0;
}
🍃获取堆的数据个数
- 对形参判空
- 然后返回size
int HeapSize(Heap* hp)//堆的数据个数
{
assert(hp);
return hp->size;
}
六、C语言实现堆的代码示例
🍃Heap.h //堆的头文件
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
typedef int HPDataType;//数据类型重定义
typedef struct Heap//堆的结构定义
{
HPDataType* a;
int size;
int capacity;
}Heap;
//堆的初始化
void HeapInit(Heap* php);
// 堆的销毁
void HeapDestory(Heap* hp);
//向上调整算法
void Adjustup(HPDataType* a, int child);
//交换函数
void Swap(HPDataType* a, HPDataType* b);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 向下调整算法
void Adjustdown(HPDataType* a, int parent, int n);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
🍃Heap.c //堆的源文件
#include"Heap.h"
void HeapInit(Heap* php)//初始化
{
assert(php);
php->a = NULL;
php->size = php->capacity = 0;
}
// 堆的销毁
void HeapDestory(Heap* hp)//销毁
{
assert(hp);
free(hp->a);
hp->a = NULL;
hp->size = hp->capacity = 0;
}
void Swap(HPDataType* a, HPDataType* b)//交换函数
{
HPDataType tmp = *a;
*a = *b;
*b = tmp;
}
void Adjustup(HPDataType* a, int child)//向上调整算法
{
assert(a);//数组必须存在,否则解引用就会报错
int parent = (child - 1) / 2;
while (child > 0 && a[parent] > a[child])//这里以小堆调整为例
{
Swap(&a[parent], &a[child]);//交换数据必须传地址
child = parent;
parent= (child - 1) / 2;
}
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)//入堆
{
assert(hp);//接收的堆地址必须是有效的
if (hp->size == hp->capacity)//判断是否需要扩容
{
int newcapacity = hp->capacity == 0 ? 4 : (hp->capacity) * 2;
HPDataType* tmp = (HPDataType*)realloc(hp->a,sizeof(HPDataType) * newcapacity);
if (tmp == NULL)
{
perror("Push perror\n");
exit(1);
}
hp->a = tmp;
hp->capacity = newcapacity;
}
hp->a[hp->size++] = x;//插入到尾部
Adjustup(hp->a, hp->size - 1);//进行向上调整
}
void Adjustdown(HPDataType* a, int parent, int n)//向下调整算法
{
assert(a);
int child = parent * 2 + 1;//先假设左孩子小
while (child < n)
{
if (child + 1 < n && a[child + 1] < a[child])//这里以小堆调整为例
child++;//如果右孩子存在,且右孩子小,父节点与右孩子进行比较
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
void HeapPop(Heap* hp)//出堆
{
assert(hp);
assert(hp->size);//判断堆不为空
Swap(&(hp->a[0]), &(hp->a[hp->size - 1]));
hp->size--;//第一个数据与最后一个数据交换,然后删除最后一个
Adjustdown(hp->a, 0, hp->size);
}
HPDataType HeapTop(Heap* hp)// 取堆顶的数据
{
assert(hp);
assert(hp->size);
return hp->a[0];
}
int HeapSize(Heap* hp)//堆的数据个数
{
assert(hp);
return hp->size;
}
int HeapEmpty(Heap* hp)//堆的判空
{
assert(hp);
return hp->size == 0;
}
🍃test.c //mian函数测试文件
#include"Heap.h"
void test1()
{
Heap hp;
HeapInit(&hp);//初始化
if (HeapEmpty(&hp))
printf("堆空\n");
else
printf("堆非空\n");
int arr[] = { 5,7,8,11,2,9,15,13,21};
for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)//数据入堆
{
HeapPush(&hp, arr[i]);
}
if (HeapEmpty(&hp))
printf("堆空\n");
else
printf("堆非空\n");
printf("堆的数据个数:%d\n", HeapSize(&hp));
while (hp.size)//每次打印堆顶元素,并出堆
{
printf("%d ", HeapTop(&hp));
HeapPop(&hp);
}
printf("堆的数据个数:%d\n", HeapSize(&hp));
HeapDestory(&hp);
}
int main()
{
test1();
return 0;
}
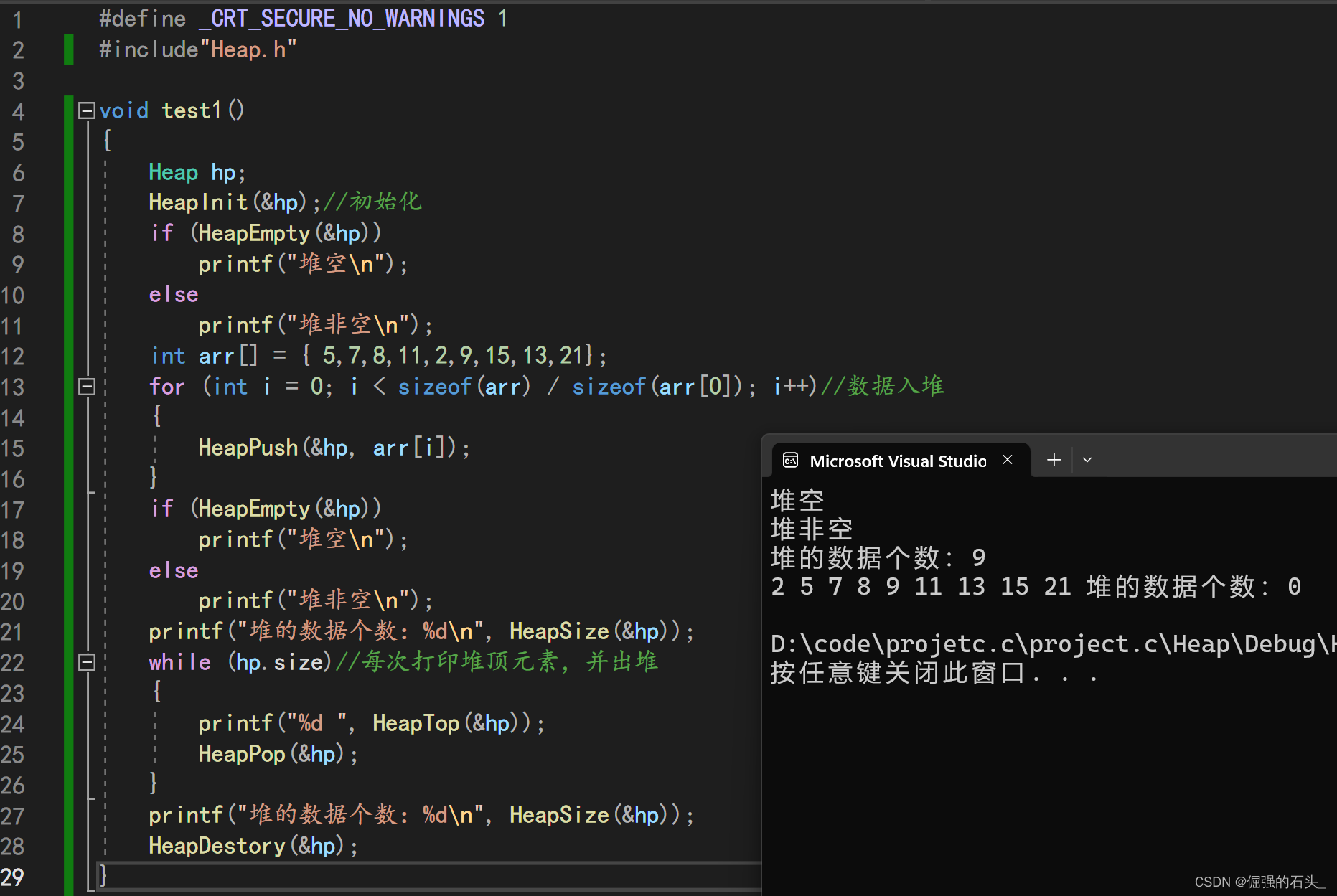
🍃测试结果
七、性能分析
- 堆的插入和删除操作的时间复杂度均为O(log n),这使得堆在处理大规模数据时具有较高的效率。
- 与其他数据结构(如链表)相比,数组在实现堆时具有更好的空间利用率和访问速度。
八、应用场景
- 优先队列:堆可以高效地实现优先队列,支持按照元素的优先级进行插入和删除操作。
- 堆排序:堆排序是一种基于堆的排序算法,具有O(nlogn)的时间复杂度。
- 数据流中的TopK问题:在处理数据流时,可以使用堆来快速找到前K大或前K小的元素。
九、总结
本文详细介绍了数组在堆数据结构中的妙用,并通过具体的代码示例和性能分析展示了其高效性和灵活性。通过深入学习堆的概念和实现方法,我们可以更好地理解其原理和应用场景,并在实际编程中灵活运用堆数据结构来解决各种问题。
如果看完本篇文章对您有所帮助,麻烦三连支持一下