《昇思25天学习打卡营第6天 | 函数式自动微分》
目录
- 《昇思25天学习打卡营第6天 | 函数式自动微分》
- 函数式自动微分
- 简单的单层线性变换模型
- 函数与计算图
- 微分函数与梯度计算
- Stop Gradient
函数式自动微分
神经网络的训练主要使用反向传播算法,模型预测值(logits)与正确标签(label)送入损失函数(loss function)获得loss,然后进行反向传播计算,求得梯度(gradients),最终更新至模型参数(parameters)。自动微分能够计算可导函数在某点处的导数值,是反向传播算法的一般化。自动微分主要解决的问题是将一个复杂的数学运算分解为一系列简单的基本运算,该功能对用户屏蔽了大量的求导细节和过程,大大降低了框架的使用门槛。
MindSpore使用函数式自动微分的设计理念,提供更接近于数学语义的自动微分接口grad和value_and_grad。
简单的单层线性变换模型
我们通过学习使用一个简单的单层线性变换模型来了解
import numpy as np
import mindspore
from mindspore import nn
from mindspore import ops
from mindspore import Tensor, Parameter
函数与计算图
计算图是用图论语言表示数学函数的一种方式,也是深度学习框架表达神经网络模型的统一方法。我们将根据下面的计算图构造计算函数和神经网络。
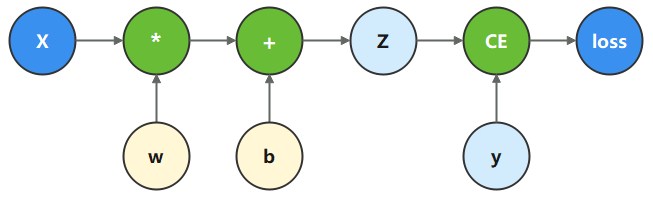
在这个模型中, 𝑥
为输入, 𝑦
为正确值, 𝑤
和 𝑏
是我们需要优化的参数。
x = ops.ones(5, mindspore.float32) # input tensor
y = ops.zeros(3, mindspore.float32) # expected output
w = Parameter(Tensor(np.random.randn(5, 3), mindspore.float32), name='w') # weight
b = Parameter(Tensor(np.random.randn(3,), mindspore.float32), name='b') # bias
我们根据计算图描述的计算过程,构造计算函数。 其中,binary_cross_entropy_with_logits 是一个损失函数,计算预测值和目标值之间的二值交叉熵损失。
def function(x, y, w, b):
z = ops.matmul(x, w) + b
loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
return loss
执行计算函数,可以获得计算的loss值。
loss = function(x, y, w, b)
print(loss)
Tensor(shape=[], dtype=Float32, value= 0.914285)
微分函数与梯度计算
为了优化模型参数,需要求参数对loss的导数:
∂
loss
∂
w
\frac{\partial \operatorname{loss}}{\partial w}
∂w∂loss和
∂
loss
∂
b
\frac{\partial \operatorname{loss}}{\partial b}
∂b∂loss,此时我们调用mindspore.grad函数,来获得function的微分函数。
这里使用了grad函数的两个入参,分别为:
fn:待求导的函数。grad_position:指定求导输入位置的索引。
由于我们对
w
w
w和
b
b
b求导,因此配置其在function入参对应的位置(2, 3)。
使用
grad获得微分函数是一种函数变换,即输入为函数,输出也为函数。
grad_fn = mindspore.grad(function, (2, 3))
执行微分函数,即可获得 𝑤
、 𝑏
对应的梯度。
grads = grad_fn(x, y, w, b)
print(grads)
(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 6.56869709e-02, 5.37334494e-02, 3.01467031e-01],
[ 6.56869709e-02, 5.37334494e-02, 3.01467031e-01],
[ 6.56869709e-02, 5.37334494e-02, 3.01467031e-01],
[ 6.56869709e-02, 5.37334494e-02, 3.01467031e-01],
[ 6.56869709e-02, 5.37334494e-02, 3.01467031e-01]]),
Tensor(shape=[3], dtype=Float32, value= [ 6.56869709e-02, 5.37334494e-02, 3.01467031e-01]))
Stop Gradient
通常情况下,求导时会求loss对参数的导数,因此函数的输出只有loss一项。当我们希望函数输出多项时,微分函数会求所有输出项对参数的导数。此时如果想实现对某个输出项的梯度截断,或消除某个Tensor对梯度的影响,需要用到Stop Gradient操作。
这里我们将function改为同时输出loss和z的function_with_logits,获得微分函数并执行。
def function_with_logits(x, y, w, b):
z = ops.matmul(x, w) + b
loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
return loss, z
grad_fn = mindspore.grad(function_with_logits, (2, 3))
grads = grad_fn(x, y, w, b)
print(grads)
(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 1.06568694e+00, 1.05373347e+00, 1.30146706e+00],
[ 1.06568694e+00, 1.05373347e+00, 1.30146706e+00],
[ 1.06568694e+00, 1.05373347e+00, 1.30146706e+00],
[ 1.06568694e+00, 1.05373347e+00, 1.30146706e+00],
[ 1.06568694e+00, 1.05373347e+00, 1.30146706e+00]]),
Tensor(shape=[3], dtype=Float32, value= [ 1.06568694e+00, 1.05373347e+00, 1.30146706e+00]))
可以看到求得
w
w
w、
b
b
b对应的梯度值发生了变化。此时如果想要屏蔽掉z对梯度的影响,即仍只求参数对loss的导数,可以使用ops.stop_gradient接口,将梯度在此处截断。我们将function实现加入stop_gradient,并执行。
def function_stop_gradient(x, y, w, b):
z = ops.matmul(x, w) + b
loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
return loss, ops.stop_gradient(z)
grad_fn = mindspore.grad(function_stop_gradient, (2, 3))
grads = grad_fn(x, y, w, b)
print(grads)



![[AIGC] Shell脚本在工作中的常用用法](https://img-blog.csdnimg.cn/img_convert/2110cabb1a7f0a98c7edabb00b2b1ba3.jpeg)