今天下起了暴雨,本以为下午就可以结束的答辩又因为老师开会被推迟。研三的学长走了后我们开始了0元购,收获颇丰哈哈,做个题
1、题目描述
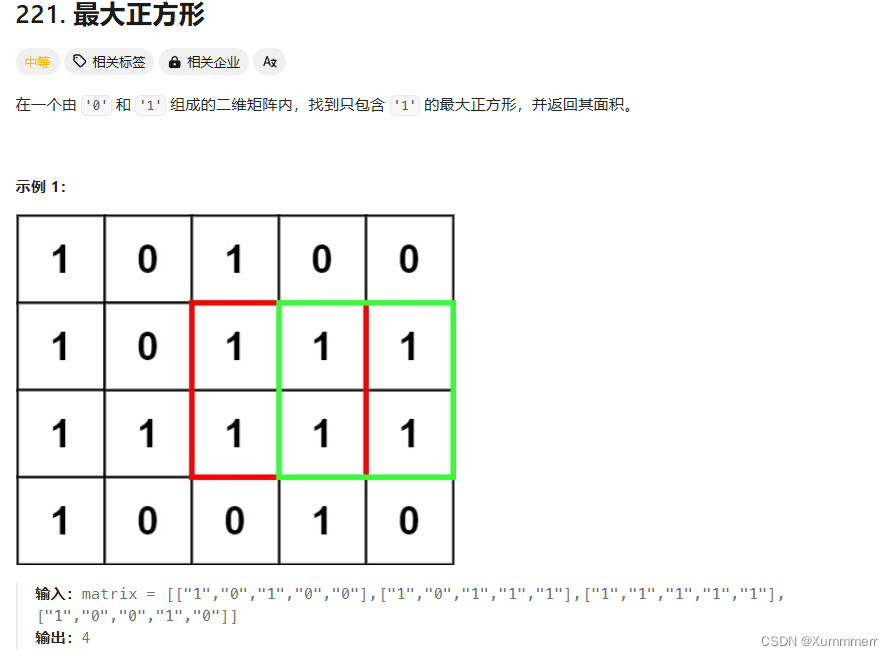
2、算法分析
给定一个矩形,要求最大正方形。第一次见这种题目哈
2024 6/30 嘿嘿,这道题我昨天没做啦,今天来做,今天中午就待实验室啦,回去太麻烦了。那么继续开始做题
我拿到这个题大概知道跟动态规划有关,然后看了题解,题解给出两种算法:暴力与DP。那么我们先来看看暴力解法
暴力法是最简单直观的做法,具体做法如下:
- 遍历矩阵中的每个元素,每次遇到 1,则将该元素作为正方形的左上角;
- 确定正方形的左上角后,根据左上角所在的行和列计算可能的最大正方形的边长(正方形的范围不能超出矩阵的行数和列数),在该边长范围内寻找只包含 1 的最大正方形;
- 每次在下方新增一行以及在右方新增一列,判断新增的行和列是否满足所有元素都是 1。
代码演示:
public int maximalSquare(char[][] matrix) {
// 初始化最大正方形的边长为0
int maxSide = 0;
// 如果矩阵为空,则直接返回0
if(matrix == null || matrix.length == 0 || matrix[0].length == 0){
return maxSide;
}
// 获取矩阵的行数和列数
int rows = matrix.length, columns = matrix[0].length;
// 遍历矩阵中的每个元素
for(int i = 0; i < rows; i++){
for(int j = 0; j < columns ; j++){
// 如果当前元素是'1',则开始尝试以当前位置为左上角的最大正方形的边长
if(matrix[i][j] == '1'){
// 更新maxSide,因为至少可以形成一个边长为1的正方形
maxSide = Math.max(maxSide, 1);
// 计算当前位置可能形成的最大正方形的最大可能边长
// 不能超过矩阵的边界
int currentMaxSide = Math.min(rows - i, columns - j );
// 尝试从边长为1开始,逐渐扩大正方形的边长
for(int k = 1; k < currentMaxSide; k++){
// 假设当前边长k的正方形是可能的
boolean flag = true;
// 检查正方形的右下角是否为'0',如果是,则无法形成边长为k的正方形
if(matrix[i + k][j + k] == '0'){
break;
}
// 检查正方形的右侧和下方的边界是否都为'1'
// 如果有任何一个为'0',则无法形成边长为k的正方形
for(int m = 0; m < k; m++){
if(matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0'){
flag = false;
break;
}
}
// 如果能形成边长为k的正方形,则更新maxSide
if(flag){
maxSide = Math.max(maxSide, k + 1);
// 如果不能形成边长为k的正方形,则无需继续尝试更大的边长
}else{
break;
}
}
}
}
}
// 计算最大正方形的面积并返回
int maxSquare = maxSide * maxSide;
return maxSquare;
}
暴力解法的时间复杂度: O ( m n min ( m , n ) 2 ) O(mn\min(m,n)^2) O(mnmin(m,n)2),其中 m 和 n 是矩阵的行数和列数。空间复杂度:O(1)。额外使用的空间复杂度为常数。
可以看到空间复杂度很高了,那么我们来看看动态规划是怎么解决的。
可以使用动态规划降低时间复杂度。
- 我们用
dp(i,j)表示以(i,j)为右下角,且只包含1的正方形的边长最大值。如果我们能计算出所有
dp(i,j)的值,那么其中的最大值即为矩阵中只包含1的正方形的边长最大值,其平方即为最大正方形的面积。 - 那么如何计算
dp中的每个元素值呢?对于每个位置(i,j),检查在矩阵中该位置的值: - 如果该位置的值是
0,则dp(i,j)=0,因为当前位置不可能在由1组成的正方形中; - 如果该位置的值是
1,则dp(i,j)的值由其上方、左方和左上方的三个相邻位置的dp值决定。具体而言,当前位置的元素值等于三个相邻位置的元素中的最小值加 1,状态转移方程如下:
dp(i,j) = min(dp(i − 1,j), dp(i − 1,j − 1), dp(i,j − 1) ) + 1
此外,还需要考虑边界条件。如果 i 和 j 中至少有一个为 0,则以位置 (i,j) 为右下角的最大正方形的边长只能是 1,因此 dp(i,j)=1。
3、代码
public int maximalSquare(char[][] matrix) {
// 初始化最大正方形的边长为0
int maxSide = 0;
// 如果矩阵为空,或者没有行或列,则直接返回0
if(matrix == null || matrix.length == 0 || matrix[0].length == 0){
return maxSide;
}
// 获取矩阵的行数和列数
int rows = matrix.length, columns = matrix[0].length;
// 创建一个与原始矩阵大小相同的二维dp数组,用于存储每个位置的最大正方形边长
int[][] dp = new int[rows][columns];
// 遍历矩阵的每一个位置
for(int i = 0; i < rows; i++){
for(int j = 0 ; j < columns; j++){
// 如果当前位置是'1'
if(matrix[i][j] == '1'){
// 如果当前位置是第一行或第一列,则最大正方形边长只能是1
if(i == 0 || j == 0){
dp[i][j] = 1;
}else{
// 否则,当前位置的最大正方形边长取决于其上方、左方和左上方的最小边长,并加1
// 因为我们要考虑的是由'1'组成的正方形
dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
}
// 更新最大正方形的边长
maxSide = Math.max(maxSide, dp[i][j]);
}
}
}
// 计算最大正方形的面积(边长的平方)
int maxSquare = maxSide * maxSide;
// 返回最大正方形的面积
return maxSquare;
}
这里的dp思想跟我之前做的一道最短路径思想是一样的。通过填充一个与原始矩阵大小相同的dp数组来记录每个位置的最大正方形边长。最终,返回的是最大正方形的面积,而不是边长。
4、复杂度分析
- 时间复杂度:
O(mn),其中 m 和 n 是矩阵的行数和列数。需要遍历原始矩阵中的每个元素计算 dp 的值。 - 空间复杂度:
O(mn),其中 m 和 n 是矩阵的行数和列数。创建了一个和原始矩阵大小相同的矩阵 dp。由于状态转移方程中的 dp(i,j) 由其上方、左方和左上方的三个相邻位置的 dp 值决定,因此可以使用两个一维数组进行状态转移,空间复杂度优化至 O(n)。