第24天,回溯算法part03,牢记回溯三部曲,掌握树形结构结题方法💪
目录
93.复原IP地址
78.子集
90.子集II
总结
93.复原IP地址
文档讲解:代码随想录复原IP地址
视频讲解:手撕复原IP地址
题目:

学习:本题属于切割类问题,不同的是本题需要使用 ' · ’ 来切割,并且本题对切割的数字大小和多少,切割多少次都有要求。但本质都是两步:1.切割;2.判断切割是否正确。
依据以上两点,本题和131.分割回文串不同的地方就在于对分割部分的判断和终止条件的选择。回溯逻辑用树形结构来表示为:
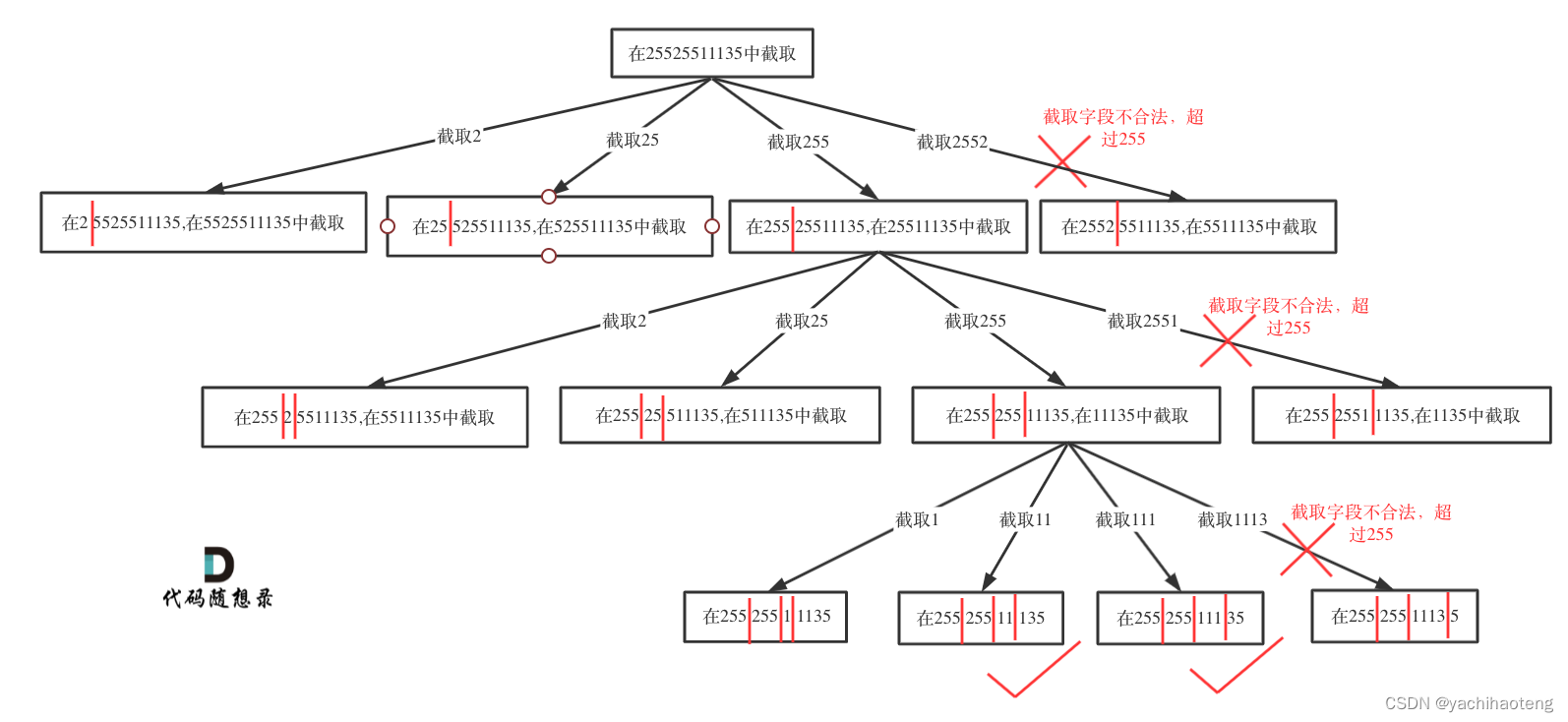
注意:判断分割部分是否合法,主要从三个部分出发:1.段位以0为开头且不止有0的数字不合法。2.段位里有非正整数字符不合法。3.段位如果大于255了不合法。
代码:确定回溯三部曲,注意本题要在字符串中加入' . ' 因此回溯的时候要删掉该点。
//时间复杂度O(3^4)
//空间复杂度O(n)
class Solution {
public:
//直接在字符串上进行操作,因此不设置路径数组
vector<string> result; //返回数组
//确定返回值和参数列表,直接在答案数组中插入因此不需要返回值,参数中需要原字符串s,分割点startindex
//本题还需要一个int型变量point表示当前逗号的数量
void backtracking(string& s, int startindex, int point) {
//确定终止条件,当逗号数量为3个时,说明当前分割已经完成了
if(point == 3) {
//最后一部分字符串还需要进行判断
if(ipvaild(s, startindex, s.size() - 1)) {
result.push_back(s);
}
return;
}
//确定单层递归逻辑
for(int i = startindex; i < s.size(); i++) {
//startindex作为切割线,切割的字符串区间为[startindex, i],左闭右闭
//判断切割下来的字符串是否合理
if(ipvaild(s, startindex, i)){
//如果合理的话,在字符串下标i后插入逗号,并进行下一轮递归
s.insert(s.begin() + i + 1, '.');
point++;
//注意这里需要传入的是i+2,因为加了一个逗号,切割的位置需要往后移两位
backtracking(s, i + 2, point);
point--; //回溯
s.erase(s.begin() + i + 1);
}
else { //假如不满足,后续的切割方法也难以满足,直接跳出本层循环
break;
}
}
}
bool ipvaild(string& s, int start, int end) {
if (start > end) {
return false;
}
//如果存在前置0的话,返回false
if(start != end && s[start] == '0') {
return false;
}
int num = 0; //对切割字符串进行求和
for(int i = start; i <= end; i++) {
if(s[i] - '0' < 0 || s[i] - '0' > 9) {
return false;
}
num = num * 10 + (s[i] - '0');
if(num > 255) {
return false;
}
}
return true;
}
vector<string> restoreIpAddresses(string s) {
backtracking(s, 0, 0);
return result;
}
};本题可以进行剪枝,自认为本题可以从三个部分进行剪枝,分别是:1.剪枝1,给的字符串不满足切割有效的IP地址;2.剪枝2,分割实际只需要分割3个字符就行,缩小循环范围;3.每次切割后可以判断一下是否后面的字符还能够满足切割要求。
代码:
class Solution {
public:
//切割问题主要需要两点:切割,判断!
//直接在字符串上进行操作,因此不设置路径数组
vector<string> result; //返回数组
//确定返回值和参数列表,直接在答案数组中插入因此不需要返回值,参数中需要原字符串s,分割点startindex
//本题还需要一个int型变量point表示当前逗号的数量
void backtracking(string& s, int startindex, int point) {
//确定终止条件,当逗号数量为3个时,说明当前分割已经完成了
if(point == 3) {
//最后一部分字符串还需要进行判断
if(ipvaild(s, startindex, s.size() - 1)) {
result.push_back(s);
}
return;
}
//确定单层递归逻辑
//剪枝2,分割只需要分割3个数字就够了
for(int i = startindex; i < startindex + 3; i++) {
//剪枝3,后续剩余的节点数不满足切割要求
if(s.size() - startindex > (4 - point) * 3 || s.size() - startindex < (4 - point)) {
break;
}
//startindex作为切割线,切割的字符串区间为[startindex, i],左闭右闭
//判断切割下来的字符串是否合理
if(ipvaild(s, startindex, i)){
//如果合理的话,在字符串下标i后插入逗号,并进行下一轮递归
s.insert(s.begin() + i + 1, '.');
point++;
//注意这里需要传入的是i+2,因为加了一个逗号,切割的位置需要往后移两位
backtracking(s, i + 2, point);
point--; //回溯
s.erase(s.begin() + i + 1);
}
else { //假如不满足,后续的切割方法也难以满足,直接跳出本层循环
break;
}
}
}
bool ipvaild(string& s, int start, int end) {
if (start > end) {
return false;
}
//如果存在前置0的话,返回false
if(start != end && s[start] == '0') {
return false;
}
int num = 0; //对切割字符串进行求和
for(int i = start; i <= end; i++) {
if(s[i] - '0' < 0 || s[i] - '0' > 9) {
return false;
}
num = num * 10 + (s[i] - '0');
if(num > 255) {
return false;
}
}
return true;
}
vector<string> restoreIpAddresses(string s) {
//剪枝1,给的字符串不满足切割有效的ip地址
if(s.size() < 4 || s.size() > 12) return result;
backtracking(s, 0, 0);
return result;
}
};78.子集
文档讲解:代码随想录子集
视频讲解:手撕子集问题
题目:
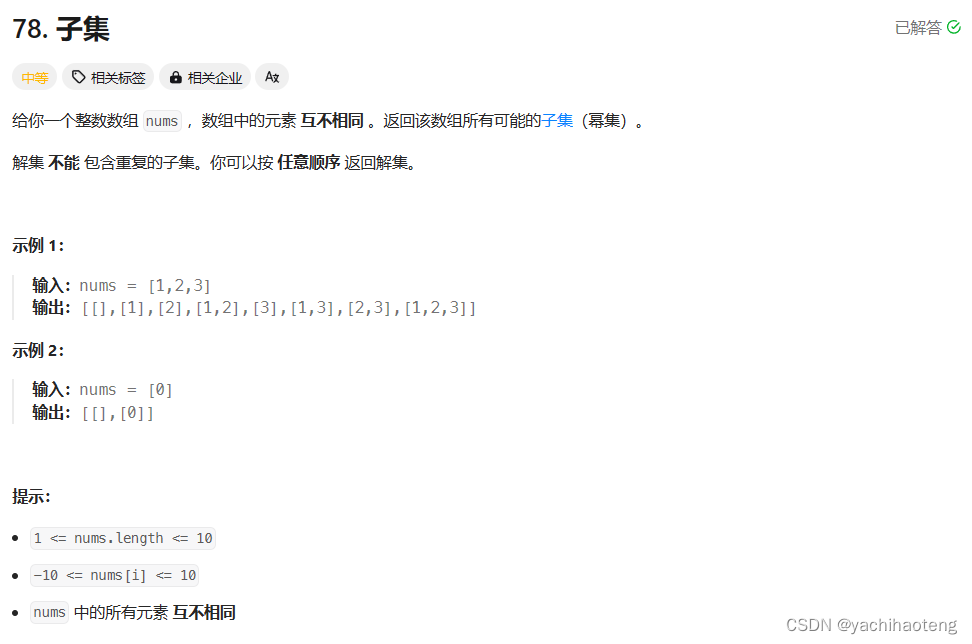
学习:回溯算法能够解决的第三类问题,子集问题。子集问题与切割问题和组合问题的本质不同在于,切割问题和组合问题都是在叶子节点收获结果,但是子集问题需要在每个节点都收获结果,这也导致了子集问题对result数组push_back的位置不同,但其他部分其实几乎是一致的。子集问题其实也能看作是一个组合问题,因此也需要注意去重。回溯逻辑转化为树形结构为:
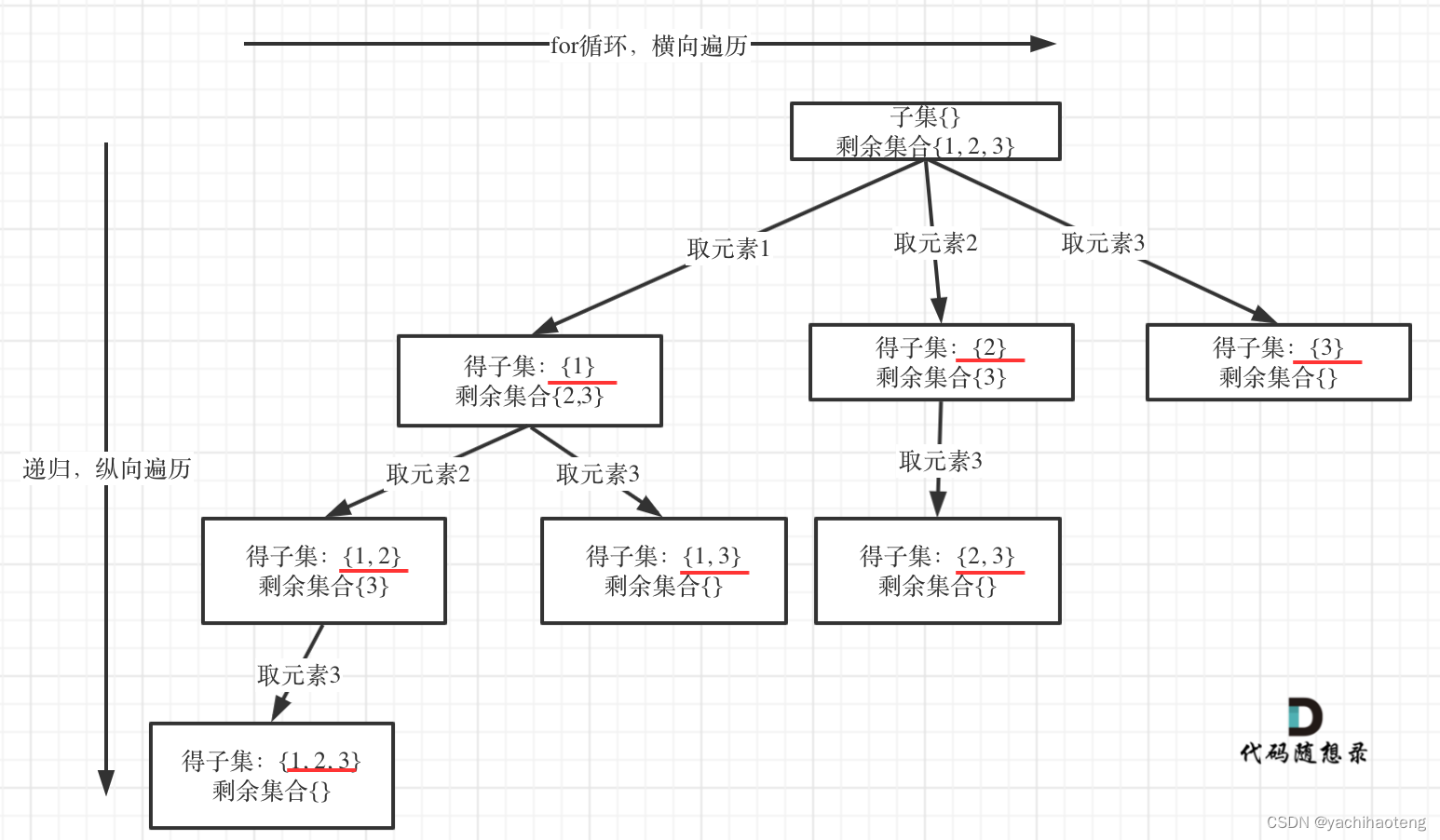
代码:确定回溯三部曲
//时间复杂度O(n*2^n)
//空间复杂度O(n)
class Solution {
public:
vector<vector<int>> result; //返回数组
vector<int> path; //保存路径
//确定返回值和参数列表,在数组中直接进行操作,所以不需要返回值,参数列表需要遍历的数组和当前遍历的下标
void backtracking(vector<int>& nums, int startindex) {
//子集问题的不同在于,子集收获答案是在每个节点均收货一次
//在终止条件前,先进行收获,其中也包含了空集
result.push_back(path);
//确定终止条件(其实等于就可以了),遍历到最后
//该终止条件也可以不写,因为当startindex >= nums.size()时,下面的for循环也不会进入,但要注意for循环后加return。
if(startindex >= nums.size()) {
return;
}
//确定单层递归逻辑
for(int i = startindex; i < nums.size(); i++) {
path.push_back(nums[i]);
//传入i+1,防止出现重复
backtracking(nums, i + 1);
path.pop_back();
}
return;
}
vector<vector<int>> subsets(vector<int>& nums) {
backtracking(nums, 0);
return result;
}
};90.子集II
文档讲解:代码随想录子集II
视频讲解:手撕子集II
题目:

学习:本题和上一题不同点在于本题存在重复元素,需要对后续的相同元素进行去重,事实上本题和组合总和II的去重是相同的,本质都是如果后面出现了与前面相同的元素就可以跳过该元素的遍历,因为前面的元素一定把后面的元素还有的组合都包括的。基于此本题可以采取和40.组合总和II相同的去重方式,都是在树层进行去重。
代码:确定回溯三部曲
//时间复杂度O(n*2^n)
//空间复杂度O(n)
class Solution {
public:
vector<vector<int>> result; //返回答案数组
vector<int> path; //保存路径
//确定参数和返回值
void backtracking(vector<int>& nums, int startindex) {
//收集每一个节点
result.push_back(path);
//确定终止条件
if(startindex == nums.size()) {
return;
}
//确定单层递归逻辑
for(int i = startindex; i < nums.size(); i++) {
//去重
if(i > startindex && nums[i] == nums[i-1]){
continue;
}
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
return;
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
//进行排序,便于去重
sort(nums.begin(), nums.end());
backtracking(nums, 0);
return result;
}
};总结
切割问题首尾,子集问题开始,牢记子集问题和切割问题和组合问题的不同。