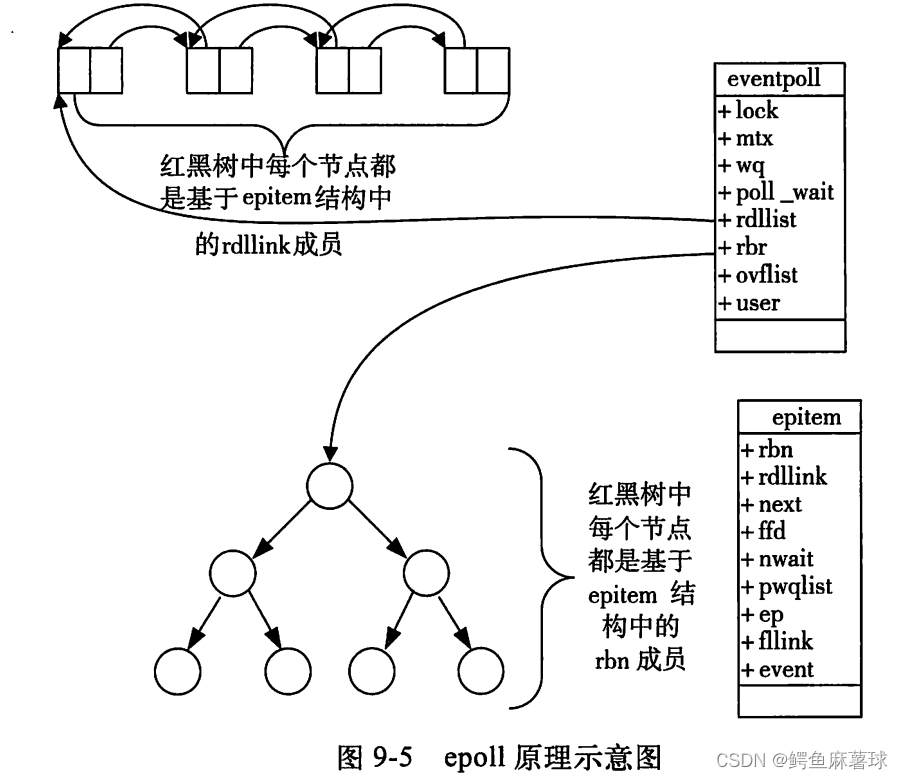
效果

原理
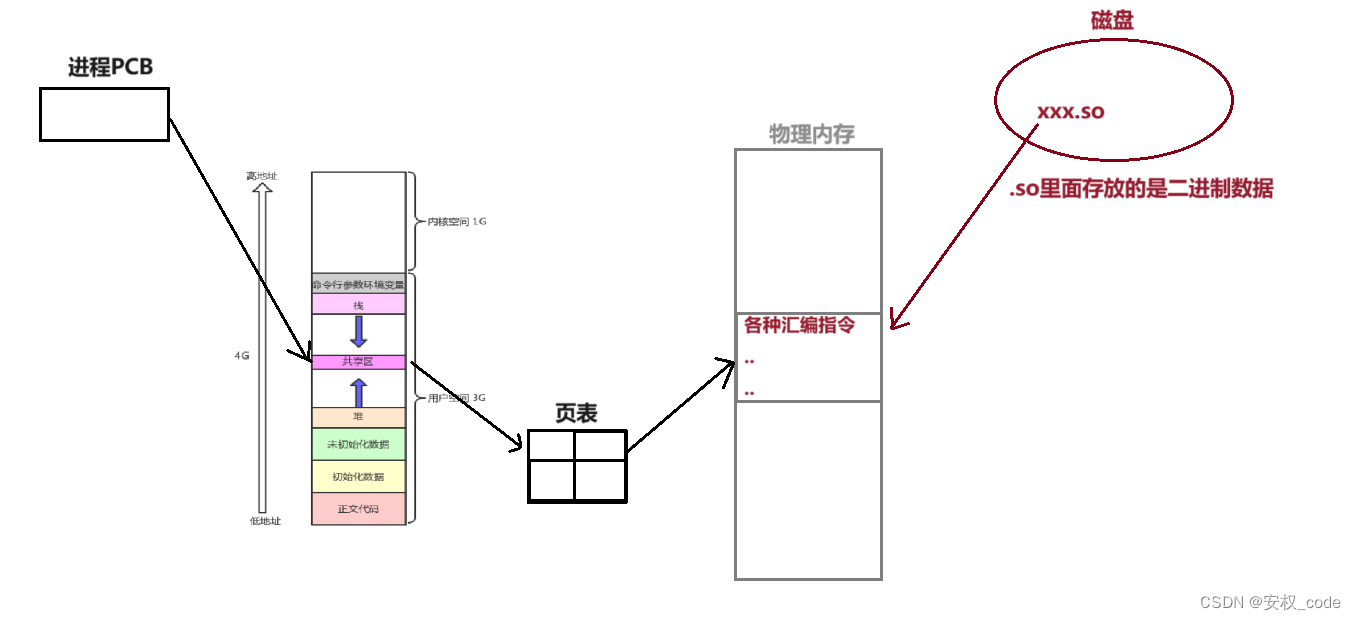
结合透视矩阵和视觉矩阵进行绘制
知识点
01透视矩阵
透视矩阵将视图空间中的坐标转换为裁剪空间中的坐标,使得更远的物体看起来更小。
function perspectiveMatrix(fov, aspect, near, far) {
const f = 1.0 / Math.tan(fov / 2);
const nf = 1 / (near - far);
return new Float32Array([
f / aspect, 0, 0, 0,
0, f, 0, 0,
0, 0, (far + near) * nf, -1,
0, 0, (2 * far * near) * nf, 0
]);
}
参数解释
函数 perspectiveMatrix 创建并返回一个透视投影矩阵,用于3D图形的透视投影。以下是每个参数的详细说明:
-
fov(Field of View, 视野):- 视野角度,即观察者在垂直方向上能够看到的视角。通常以弧度表示,角度单位可以通过
Math.PI / 180转换为弧度。 - 例如,
45 * Math.PI / 180表示45度的视角。
- 视野角度,即观察者在垂直方向上能够看到的视角。通常以弧度表示,角度单位可以通过
-
aspect(Aspect Ratio, 纵横比):- 视图的宽高比,即视图的宽度除以高度。它决定了横向和纵向的缩放比例。
- 例如,如果视口的宽度是800像素,高度是600像素,则
aspect= 800 / 600 = 4 / 3。
-
near(Near Clipping Plane, 近裁剪平面):- 近裁剪平面的距离,即从观察者到最近可见物体的距离。该值必须大于0。
- 例如,设置为0.1表示从0.1单位距离开始可见物体。
-
far(Far Clipping Plane, 远裁剪平面):- 远裁剪平面的距离,即从观察者到最远可见物体的距离。该值必须大于
near值。 - 例如,设置为100.0表示到100单位距离结束可见物体。
- 远裁剪平面的距离,即从观察者到最远可见物体的距离。该值必须大于
02视图矩阵
视图矩阵将世界空间中的坐标转换为视图空间中的坐标,表示相机的视点。
function lookAtMatrix(eye, center, up) {
const zAxis = normalize(subtractVectors(eye, center));
const xAxis = normalize(cross(up, zAxis));
const yAxis = normalize(cross(zAxis, xAxis));
return new Float32Array([
xAxis[0], yAxis[0], zAxis[0], 0,
xAxis[1], yAxis[1], zAxis[1], 0,
xAxis[2], yAxis[2], zAxis[2], 0,
-dot(xAxis, eye), -dot(yAxis, eye), -dot(zAxis, eye), 1
]);
}
function normalize(v) {
const length = Math.sqrt(v[0] * v[0] + v[1] * v[1] + v[2] * v[2]);
return [v[0] / length, v[1] / length, v[2] / length];
}
function subtractVectors(a, b) {
return [a[0] - b[0], a[1] - b[1], a[2] - b[2]];
}
function cross(a, b) {
return [
a[1] * b[2] - a[2] * b[1],
a[2] * b[0] - a[0] * b[2],
a[0] * b[1] - a[1] * b[0]
];
}
function dot(a, b) {
return a[0] * b[0] + a[1] * b[1] + a[2] * b[2];
}
参数解释
函数 lookAtMatrix 用于生成一个视图矩阵,用于将场景从世界空间转换到观察者空间。它通常用于实现相机的视图转换,使得相机看向特定的方向。这个函数的参数如下:
-
eye:- 相机的位置,表示观察者所在的点。
- 例如
[1, 1, 1]表示相机位于 (1, 1, 1) 的位置。
-
center:- 视点,表示相机所看向的目标点。
- 例如
[0, 0, 0]表示相机看向 (0, 0, 0) 的位置。
-
up:- 上方向向量,表示哪一个方向是相机的“上”方向。通常为
[0, 1, 0],表示正Y方向。
- 上方向向量,表示哪一个方向是相机的“上”方向。通常为
函数 lookAtMatrix 用于生成一个视图矩阵,用于将场景从世界空间转换到观察者空间。它通常用于实现相机的视图转换,使得相机看向特定的方向。这个函数的参数如下:
eye:
相机的位置,表示观察者所在的点。
例如 [1, 1, 1] 表示相机位于 (1, 1, 1) 的位置。
center:
视点,表示相机所看向的目标点。
例如 [0, 0, 0] 表示相机看向 (0, 0, 0) 的位置。
up:
上方向向量,表示哪一个方向是相机的“上”方向。通常为 [0, 1, 0],表示正Y方向。逻辑
设置透视矩阵和视觉矩阵
代码
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<title>立方体绘制</title>
<style>
* {
margin: 0;
padding: 0;
}
canvas {
margin: 50px auto 0;
display: block;
background: yellow;
}
</style>
<script src="test.js"></script>
</head>
<body>
<canvas id="canvas" width="400" height="400"></canvas>
<script>
// 获取
const canvas = document.getElementById('canvas')
const gl = canvas.getContext('webgl')
// 定义片源着色器和顶点着色器
const vsSource = `
attribute vec4 apos;
attribute vec4 acolor;
varying vec4 vcolor;
uniform mat4 u_projectionMatrix;
uniform mat4 u_viewMatrix;
void main() {
gl_Position =u_projectionMatrix * u_viewMatrix * apos;
vcolor = acolor;
}
`
const fsSource = `
precision mediump float;
varying vec4 vcolor;
void main() {
gl_FragColor = vcolor;
}
`
// 初始化webgl
const program = initShader(gl, vsSource, fsSource)
gl.useProgram(program)
// 获取 uniform 位置
const u_projectionMatrixLocation = gl.getUniformLocation(program, 'u_projectionMatrix')
const u_viewMatrixLocation = gl.getUniformLocation(program, 'u_viewMatrix')
// 创建透视矩阵和视图矩阵
const fov = Math.PI / 4 // 45度视角
const aspect = canvas.width / canvas.height
const near = 0.1
const far = 10.0
// lookAtMatrix 函数通过计算相机的位置、目标点和上方向,生成一个视图矩阵
const projectionMatrix = perspectiveMatrix(fov, aspect, near, far)
const viewMatrix = lookAtMatrix([3, 1, 7], [0, 0, 0], [0, 1, 0])
function lookAtMatrix(eye, center, up) {
const zAxis = normalize(subtractVectors(eye, center))
const xAxis = normalize(cross(up, zAxis))
const yAxis = normalize(cross(zAxis, xAxis))
return new Float32Array([
xAxis[0],
yAxis[0],
zAxis[0],
0,
xAxis[1],
yAxis[1],
zAxis[1],
0,
xAxis[2],
yAxis[2],
zAxis[2],
0,
-dot(xAxis, eye),
-dot(yAxis, eye),
-dot(zAxis, eye),
1
])
}
function normalize(v) {
const length = Math.sqrt(v[0] * v[0] + v[1] * v[1] + v[2] * v[2])
return [v[0] / length, v[1] / length, v[2] / length]
}
function subtractVectors(a, b) {
return [a[0] - b[0], a[1] - b[1], a[2] - b[2]]
}
function cross(a, b) {
return [a[1] * b[2] - a[2] * b[1], a[2] * b[0] - a[0] * b[2], a[0] * b[1] - a[1] * b[0]]
}
function dot(a, b) {
return a[0] * b[0] + a[1] * b[1] + a[2] * b[2]
}
function perspectiveMatrix(fov, aspect, near, far) {
const f = 1.0 / Math.tan(fov / 2)
const nf = 1 / (near - far)
return new Float32Array([f / aspect, 0, 0, 0, 0, f, 0, 0, 0, 0, (far + near) * nf, -1, 0, 0, 2 * far * near * nf, 0])
}
// 设置投影矩阵和视图矩阵
gl.uniformMatrix4fv(u_projectionMatrixLocation, false, projectionMatrix)
gl.uniformMatrix4fv(u_viewMatrixLocation, false, viewMatrix)
// 创建缓存区
function initBuffer(gl, program) {
const aposLocation = gl.getAttribLocation(program, 'apos')
const acolorLocation = gl.getAttribLocation(program, 'acolor')
const verticesColors = new Float32Array([
// 前面 (红色)
-0.5,
-0.5,
0.5,
1,
0,
0,
1, // 左下
0.5,
-0.5,
0.5,
1,
0,
0,
1, // 右下
0.5,
0.5,
0.5,
1,
0,
0,
1, // 右上
-0.5,
0.5,
0.5,
1,
0,
0,
1, // 左上
// 后面 (绿色)
-0.5,
0.5,
-0.5,
0,
1,
0,
1, // 左上
-0.5,
-0.5,
-0.5,
0,
1,
0,
1, // 左下
0.5,
-0.5,
-0.5,
0,
1,
0,
1, // 右下
0.5,
0.5,
-0.5,
0,
1,
0,
1, // 右上
// 左面 (蓝色)
-0.5,
-0.5,
-0.5,
0,
0,
1,
1, // 后下
-0.5,
0.5,
-0.5,
0,
0,
1,
1, // 后上
-0.5,
0.5,
0.5,
0,
0,
1,
1, // 前上
-0.5,
-0.5,
0.5,
0,
0,
1,
1, // 前下
// 右面 (洋红色)
0.5,
-0.5,
-0.5,
1,
0,
1,
1, // 后下
0.5,
0.5,
-0.5,
1,
0,
1,
1, // 后上
0.5,
0.5,
0.5,
1,
0,
1,
1, // 前上
0.5,
-0.5,
0.5,
1,
0,
1,
1, // 前下
// 顶面 (黄色)
-0.5,
0.5,
0.5,
1,
1,
0,
1, // 前左
0.5,
0.5,
0.5,
1,
1,
0,
1, // 前右
0.5,
0.5,
-0.5,
1,
1,
0,
1, // 后右
-0.5,
0.5,
-0.5,
1,
1,
0,
1, // 后左
// 底面 (青色)
-0.5,
-0.5,
0.5,
0,
1,
1,
1, // 前左
0.5,
-0.5,
0.5,
0,
1,
1,
1, // 前右
0.5,
-0.5,
-0.5,
0,
1,
1,
1, // 后右
-0.5,
-0.5,
-0.5,
0,
1,
1,
1 // 后左
])
const indices = new Uint16Array([
// 前面
0, 1, 2, 0, 2, 3,
// 后面
4, 5, 6, 4, 6, 7,
// 左面
8, 9, 10, 8, 10, 11,
// 右面
12, 13, 14, 12, 14, 15,
// 顶面
16, 17, 18, 16, 18, 19,
// 底面
20, 21, 22, 20, 22, 23
])
const vertexColorBuffer = gl.createBuffer()
gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorBuffer)
gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW)
const indexBuffer = gl.createBuffer()
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer)
gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW)
const FSIZE = verticesColors.BYTES_PER_ELEMENT
// 启用顶点属性并指向顶点缓冲区中的数据
gl.vertexAttribPointer(aposLocation, 3, gl.FLOAT, false, FSIZE * 7, 0)
gl.enableVertexAttribArray(aposLocation)
gl.vertexAttribPointer(acolorLocation, 4, gl.FLOAT, false, FSIZE * 7, FSIZE * 3)
gl.enableVertexAttribArray(acolorLocation)
}
initBuffer(gl, program)
// 启用深度测试
// 清除缓冲区时同时清除颜色缓冲区和深度缓冲区:
gl.enable(gl.DEPTH_TEST)
gl.clearColor(0, 0, 0, 1)
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT)
gl.drawElements(gl.TRIANGLES, 36, gl.UNSIGNED_SHORT, 0)
</script>
</body>
</html>



![[知识点篇]《计算机组成原理》之数据信息的表示](https://img-blog.csdnimg.cn/direct/7a13f06023f14dc8be988aba87150599.png)