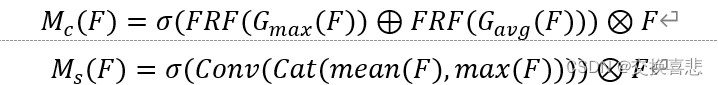参考

01背包: 每个物品只有一个, 只要选或不选两个选项

暴力解法: 回溯法枚举

1. dp[i][j]: i 表示 0 ~ i 的物品, j 表示容量, 数值表示当前的最大价值
2. 递推公式: max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])
3. 初始化: j = 0 时, 无法放任何有价值的物品, dp[i][0] = 0. i = 0时, 当空间 j 大于 物体0的价值时, 才能放该物品
4. 遍历顺序: 由于是从左上和正上方推导, 所以先遍历背包或遍历物品都可

当 i 放进去时，物品集就被分成两部分 1~i-1 和 i
若将 i 放进去，那么就把 j 空间中的 w[i] 占据, 剩下 j－w[i] 的空间给前面 i－1 ，
那么只要这时候前面 i－1 在 j－w[i] 空间里构造出最大价值, dp[i－1][j－w[i]]，再加上此时放入的i的价值v[i]，就是dp[i][j]

#include<bits/stdc++.h>
using namespace std;
int main() {
    int M, N;
    cin >> M;
    cin >> N;
    
    vector<int> weight;
    vector<int> value;
    
    for (int i = 0; i < M; i++) {
        int tem;
        cin >> tem;
        weight.push_back(tem);
    }
    
    for (int i = 0; i < M; i++) {
        int tem;
        cin >> tem;
        value.push_back(tem);
    }
 
//dp[i][j] 物品为i, j为重量 
//i索引范围[0 ~ M-1], 大小为 M
//j索引范围[0 ~ N]], 大小为 N + 1
	vector<vector<int>> dp(M, vector<int>(N + 1, 0));

    for (int j = 0; j <= N; j++) {
        if (j >= weight[0])
            dp[0][j] = value[0];
    } 

    for (int i = 1; i < M; i++) {
        for (int j = 1; j <= N; j++) { //注意取 =
            if (j - weight[i] >= 0) {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
            else {
                dp[i][j] = dp[i - 1][j];
            }
            
        }
    }
    cout << dp[M - 1][N] << endl;
}

dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

二维数组的递推公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
二维压缩成一维的递推公式: dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);//其中j是表背包容量

二维改为一维的方法:

正序遍历背包容量时, 会出现重复相加的情况, 图中为物品0不断的被累加

倒序遍历背包容量时, 由于会把本次物品的价值先加上, 价值一定比为加之前的大(dp[0~3]一定比dp[4]小), 所以不会出现重复累计的情况

#include<bits/stdc++.h>
using namespace std;

int main() {
    int M;//种类
    int N;//空间
    cin >> M;
    cin >> N;
    
    vector<int> weight(M, 0);
    vector<int> value(M, 0);
    
    for (int i = 0; i < M; i++) {
        cin >> weight[i];
    }
    for (int i = 0; i < M; i++) {
        cin >> value[i];
    }
    
    vector<int> dp(N + 1, 0);
    
    for (int i = 0; i < M; i++) {
        for (int j = N; j >=0 ; j--) {
            if (j - weight[i] >= 0) {
                dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
            } else {
                dp[j] = dp[j];
            }
            
        }
    }
    cout << dp[N] << endl;
}

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

参考

思路: 回溯法 (超时)

class Solution {
public:
    bool myoperator(int target, int sum , vector<int>& nums, int index) {
        if (sum >= target) {
            return sum == target? true : false;
        }

        bool res = false;
        for (int i = index; i < nums.size(); i++) {
            res = myoperator(target, sum + nums[i], nums, i + 1);
            if (res == true) return true;
        }
        return false;
    }
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];
        }
        if (sum % 2 == 1) return false;
        else return myoperator(sum/2, 0, nums, 0);
    }
};

思路: 01背包问题 - 每个元素只能放入一次

1. dp[j] : 容量为j, 最大价值为dp[j], 在本题中容量和价值相同
2. 递推公式:
3. dp数组如何初始化
4. 遍历顺序

能抽象成01背包最大值的原因:
5. 物品的重量和价值是相同的, dp[sum/2] 的最大值 value <= (sum/2)
6. 所以当 sum == value 时, 代表找到了一个元素

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];
        }

        if (sum % 2 == 1)
            return false;

        vector<int> dp(sum / 2 + 1, 0);
        for (int i = 0; i < nums.size(); i++) {
            for (int j = sum / 2; j >= 0; j--) {
                if (j - nums[i] >= 0) {
                    dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
                }
            }
        }
        return dp[sum / 2] == sum / 2 ? true : false;
    }
};