一、力扣64. 最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

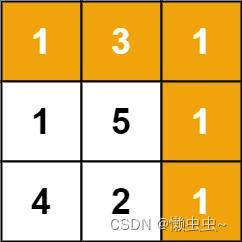
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

1.找出DP状态

此题需要求出从左上角出发，到达坐标(m,n)的路径数字和最小值。因此不难想到，子问题就是从左上角出发，到达坐标(i,j)的路径数字和最小值。

令 f[i][j]表示从左上角到坐标(i,j)的路径数字和最小值，原问题即可被划分为多个求最优值的子问题，且由于每次只能向下或向右移动一步，因此 f[i][j]的取值由f[i-1][j]和f[i][j-1]的值决定。

进一步验证，可以发现， f[i][j] 的取值与f[i-1][j]和f[i][j-1]所对应的具体路径无关。

2.找出DP状态转移方程

确定完「DP 状态」后，继续确定「DP 转移方程」。

dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]

这里需要注意边界问题，比如第一行和第一列，只能向下或者向右运动。

3. 算法实现

// 利用动态规划
    /**
     * 从左上角出发，到达坐标(i,j)的路径数字和最小值。
     * 令 f[i][j]表示从左上角到坐标(i,j)的路径数字和最小值，原问题即可被划分为多个求最优值的子问题，
     * 且由于每次只能向下或向右移动一步，因此 f[i][j]的取值由f[i-1][j]和f[i][j-1]的值决定，即符合「最优子结构原则」。
     * 进一步验证，可以发现， f[i][j] 的取值与f[i-1][j]和f[i][j-1]所对应的具体路径无关，因此符合「无后效性」。
     * 则dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
     * 这里需要注意边界问题，比如第一行和第一列，只能向下或者向右运动。
     *
     * @param grid
     * @return
     */
    public static int minPathSum(int[][] grid) {
        // 判断数据是否为空
        if(grid==null||grid.length==0||grid[0].length==0){
            return 0;
        }
        // 行
        int rows = grid.length;
        // 列
        int cols = grid[0].length;
        int[][] dp = new int[rows][cols];
        // 左上角元素值
        dp[0][0] = grid[0][0];
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if(i==0 &&j==0){
                    continue;
                }
                if(i!=0&&j==0){
                    // 第1列
                    dp[i][0] = dp[i-1][0]+grid[i][0];
                }else if(i==0&&j!=0){
                    // 第一行
                    dp[0][j] = dp[0][j-1]+grid[0][j];
                }else{
                    // 找出向下或向右的最小值+当前值
                    dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
                }
            }
        }
        return dp[rows-1][cols-1];
    }

二、力扣62. 不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

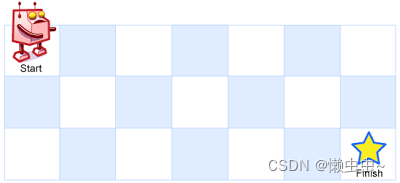
输入：m = 3, n = 7
输出：28
示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

思路1：BFS实现

    // 利用BFS实现
    public static int uniquePaths(int m, int n) {
        // 存储向右和向下两个方向
        int[][] directions = {{1, 0}, {0, 1}};
        Queue<int[]> queue = new LinkedList<>();
        // 将初始坐标加入队列
        queue.add(new int[]{0, 0});
        // 不同路径数量
        int count = 0;
        while (!queue.isEmpty()) {
            // 取出队首坐标
            int[] curr = queue.poll();
            // 坐标到达终点
            if (curr[0] == m - 1 && curr[1] == n - 1) {
                count++;
            } else {
                for (int[] direction : directions) {
                    // 遍历2个方向
                    int x = curr[0] + direction[0];
                    int y = curr[1] + direction[1];
                    if (x >= 0 && x < m && y >= 0 && y < n) {
                        // 坐标未越界，则将新坐标加入队列
                        queue.add(new int[]{x, y});
                    }
                }
            }
        }
        return count;
    }

思路2：动态规划

    // 利用动态规划实现
    public static int uniquePaths(int m, int n) {
        // 思路:由于在每个位置只能向下或者向右， 所以每个坐标的路径和等于上一行相同位置和上一列相同位置不同路径的总和，
        // 状态转移方程：f[i][j] = f[i - 1][j] + f[i][j - 1];
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; i++) {
            // 第i行，第0列，路径都是1
            dp[i][0] = 1;
        }
        for (int i = 0; i < n; i++) {
            // 第0行