双精度

Console.WriteLine("1/7的值是" + (double)1 / 7);

结果:0.14285714285714285
即使使用双精度浮点数，精确的位数也是有限的，如果想精确到小数点后100位，1000位，甚至更高哪？

朴素的除法

除数 余数 商，利用这三者的关系，可以无限度的计算下去。当然这个不能超过计算机的内存限制。
商=除数/被除数
余数 = 除数%被除数
迭代：
商 = （余数10）/被除数
余数 = (余数10）% 被除数

这就是小学数学的除法规则。基于此规则就可以不断迭代，提高精度，本文使用c#的long类型存储。用一个列表存储long。

代码实现

long的最大值是9223372036854775807 ，存在overflow的问题，因此 ，解决方案可以参见代码：

//计算1/7 除数 被除数
List<long> irrationalNumber(int divisor, int dividend) {
    List<long> longList = new List<long>();
    long final_result = 0;
    int result = 0;
    int remainder = 0;
    result = (int)divisor / dividend;
    remainder = (int)divisor% dividend;
    final_result += result;
    long tmp_result = 0;
    //这里以100为例
    while (longList.Count < 100)
    {
        divisor = remainder * 10;
        result = (int)divisor / dividend;
        remainder = (int)divisor % dividend;
        tmp_result = final_result;
        final_result = tmp_result * 10 + result;
        //判断越界9223372036854775807 4285714285714285714 越界的话 变成什么不一定 有时候是5963654709723753910，有时候是负数
        if (final_result < 0 || (long)((final_result-result))/10 != tmp_result)
        {
            longList.Add(tmp_result);
            tmp_result = 0;
            final_result = 0;
            remainder = (int)divisor / 10;
            continue;
        }
    }
    return longList;
}
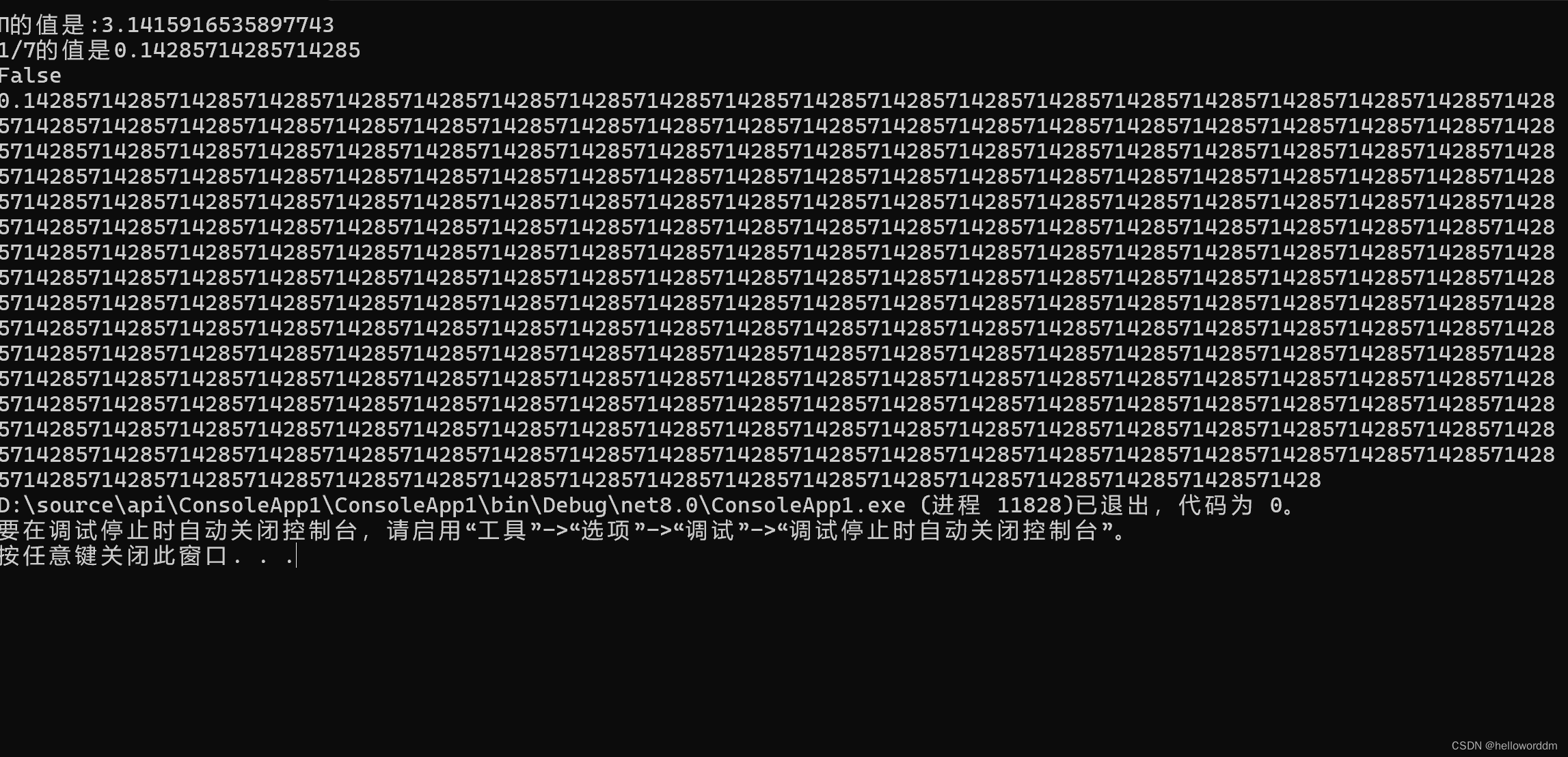
var result  =irrationalNumber(1，7);
 Console.Write("0.");
foreach (long item in result)
{
    Console.Write(item);
}

运行结果：

求16/19，只需要改为：

var result  =irrationalNumber(16，19);
 Console.Write("0.");
foreach (long item in result)
{
    Console.Write(item);
}

最终结果:

写在最后

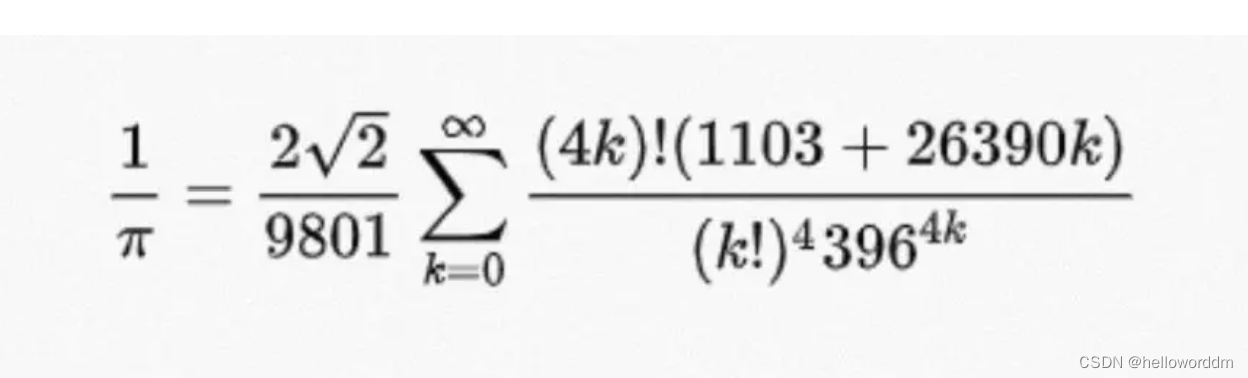
用这种方法，也可以求出Π比较高的精度。计算Π有很多方法，比如无穷级数方法，蒙特卡罗方法等

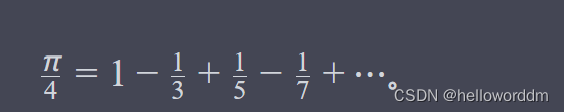
公众号

更多内容，欢迎关注我的微信公众号:半夏之夜的无情剑客。