DP:解决路径问题

文章目录

二维DP模型
如何解决路径问题
有关路径问题的几个问题
- 1.不同路径
- 2.不同路径Ⅱ
- 3.下降路径最小和
- 4.珠宝的最高价值
- 5.地下城游戏
总结

二维DP模型

二维动态规划（DP）模型是一种通过引入两个维度的状态和转移方程来解决复杂问题的技术。它在许多优化和组合问题中广泛应用，尤其是那些需要考虑二维数组或矩阵的情况。

以下是二维DP模型的核心概念和步骤：

状态定义：二维DP模型使用一个二维数组（或矩阵）来表示问题的状态。每个状态通常由两个变量（例如i和j）表示，表示在问题空间中的某个位置或状态。
状态转移方程：这是DP的核心。它描述了如何从一个状态转移到另一个状态，通常是通过递推关系来实现。转移方程基于问题的具体特性进行设计。
初始状态和边界条件：在DP表格中需要明确初始状态和边界条件。这些条件为DP表格的填充提供了起点。
目标状态：最后，我们通过目标状态来得到问题的最终解。通常是二维数组中的一个或几个特定位置。

如何解决路径问题

路径问题是动态规划中非常经典的一类问题，通常涉及从一个起点到一个终点的最短路径、最大路径或独特路径数等。解决路径问题的常用方法包括递归、回溯和动态规划（DP）。其中，动态规划由于其效率和易理解性，成为解决路径问题的常用技术。以下是解决路径问题的一些常见步骤和示例：

一般步骤

定义状态：确定DP数组的含义，通常是定义dp[i][j]表示从起点到位置(i, j)的某种路径属性（如路径和、路径数等）。
状态转移方程：建立递推关系，描述如何从一个状态转移到另一个状态。
初始化：根据问题的具体情况，设置DP数组的初始值。
计算DP数组：按照状态转移方程填充DP数组。
提取结果：通过DP数组得到最终结果。

有关路径问题的几个问题

1.不同路径

题目链接
题目：

样例输出和输入：

这道题是一个很典型的二维DP问题，也是二维DP中的路径问题的一种，这道题给定一个宽是m，长是n，让我们求在这个二位数组中从[0,0]点到[m-1,n-1]的方法有多少种。
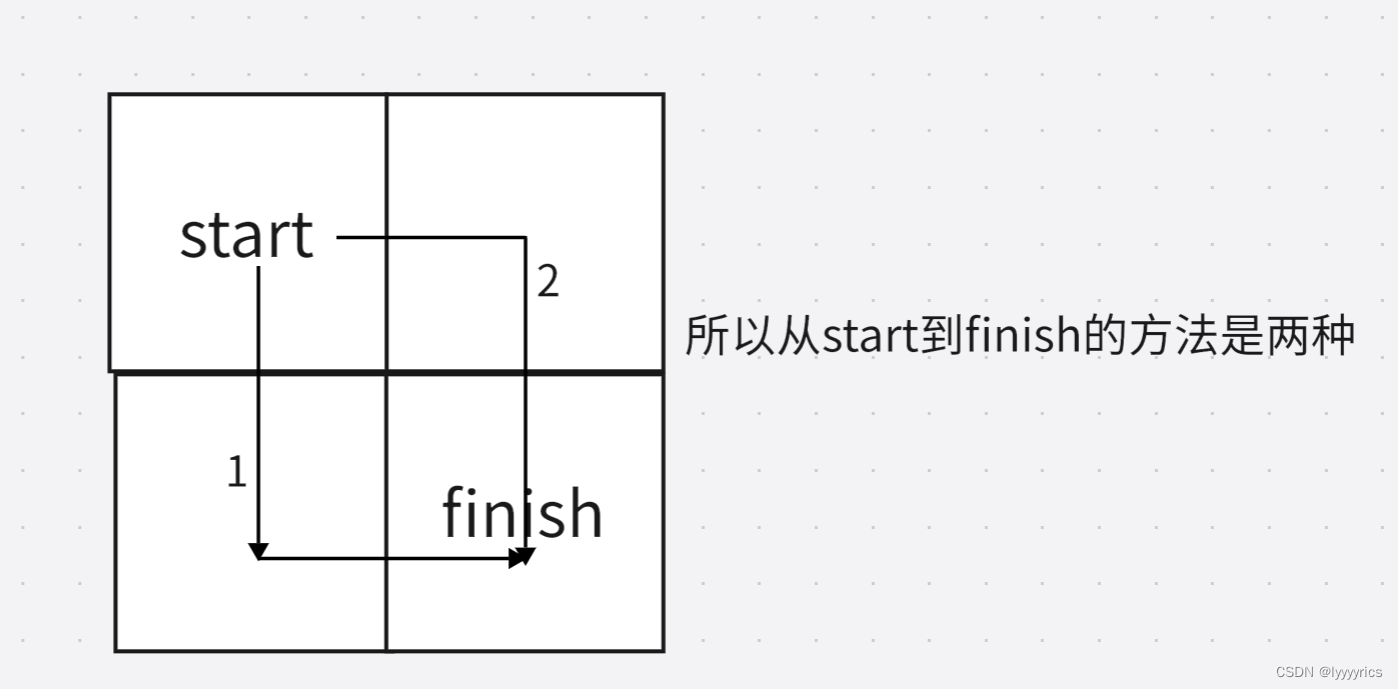
在这里插入图片描述

算法原理：
算法原理也和传统的DP问题的步骤是一样的。
第一步：状态表示，先确定dp表是初始位置还是末位置，很显然这道题要我们求的是方法有多少种，dp肯定是末位置，所以这里dp[i][j]到达[i,j]位置时有多少种方法。
第二步：状态转移方程，这道题dp表示的是到达某位置时的方法的种数，
在这里插入图片描述
很显然这道题题目要求只能向下或者向右移动，所以我们只有可能从[i,j]位置的上方或者[i,j]的左方到达[i,j]位置，所以我们需要求[i,j]位置的最多的方法数，只需要求出左边和上面的方法总数之和即可。
状态转移方程：dp[i][j]=dp[i-1][j]+dp[i][j-1]
第三步：初始化问题，这道题的当前数据需要用到左边的数据和上面的数据，所以这道题越界的地方应该是红色的地方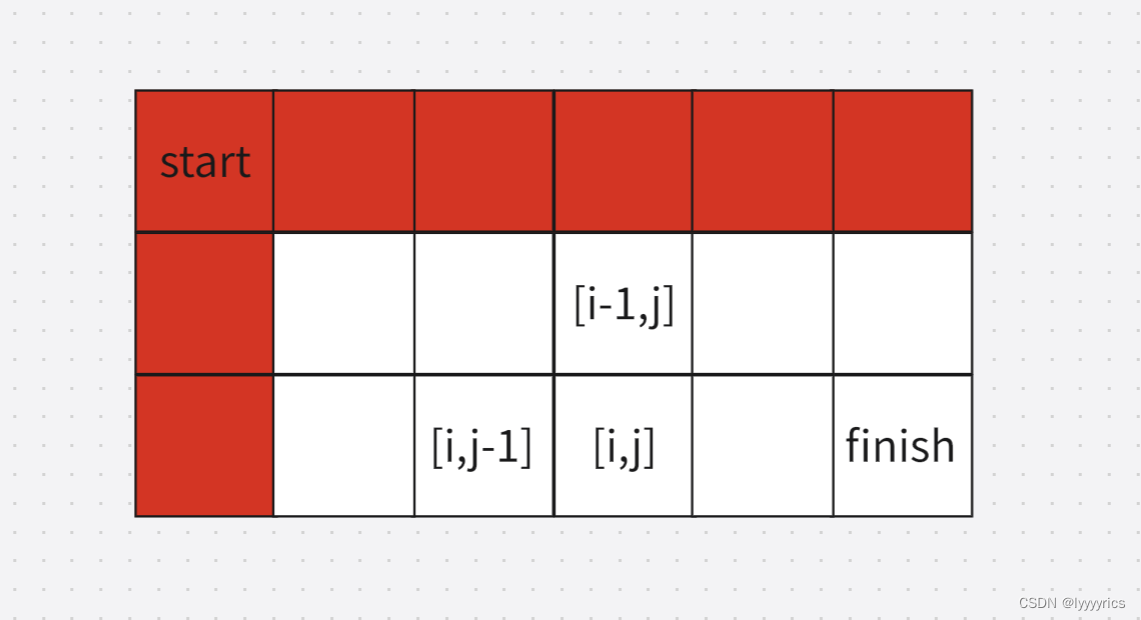：在这里插入图片描述
处理这种越界情况我们初始化只需要多开辟一行一列数组：

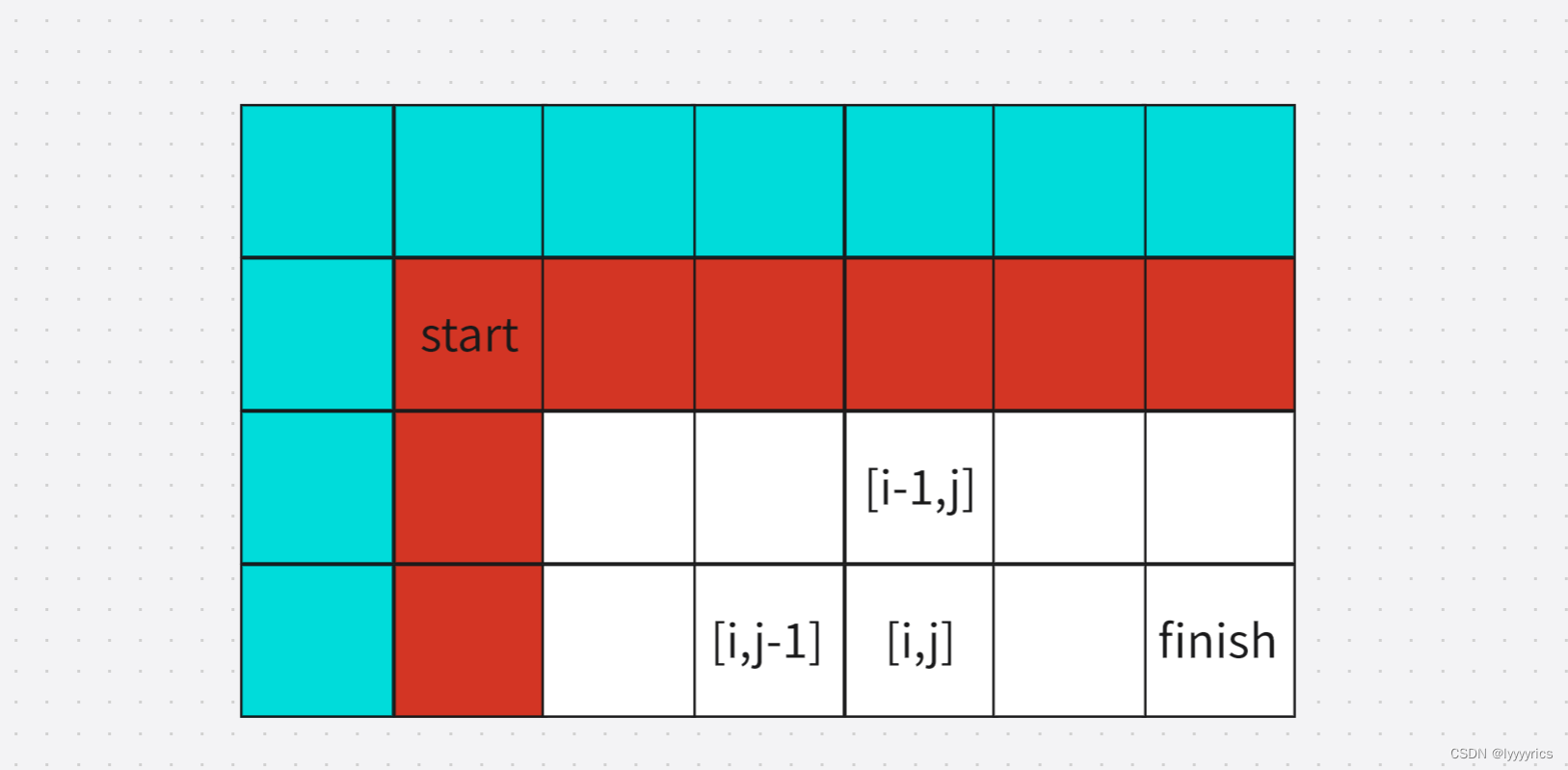
这样就不会出现越界的情况了，初始化应该把蓝色的部分全部初始化掉，具体初始哈为多少了，首先这相当于是一个虚拟的节点，为了防止越界而产生的，所以先初始化为0，但是如果初始化为零那么总的方法数就是零了，所以我们需要把[0,1]位置或者[1,0]位置初始化为1.
第四步：填表顺序，这道题很显然是从左上角开始按顺序遍历。
第五步：返回值问题，这道题求的是到达左下角的方法总数，所以是返回dp[m][n]。

代码展示：

class Solution {
public:
    int uniquePaths(int m, int n) 
    {
        //创建一个dp表，第一排和第一列表示虚拟节点
        vector<vector<int>> dp(m+1,vector<int>(n+1,0));
        //初始化[0,1]节点
        dp[0][1]=1;
        //填表
        for(int i=1;i<m+1;i++)
        {
            for(int j=1;j<n+1;j++)
            {
                //状态转移方程
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        //返回值
        return dp[m][n];
    }
};

运行结果：
在这里插入图片描述

2.不同路径Ⅱ

题目链接
题目：

样例输出和输入：

算法原理：
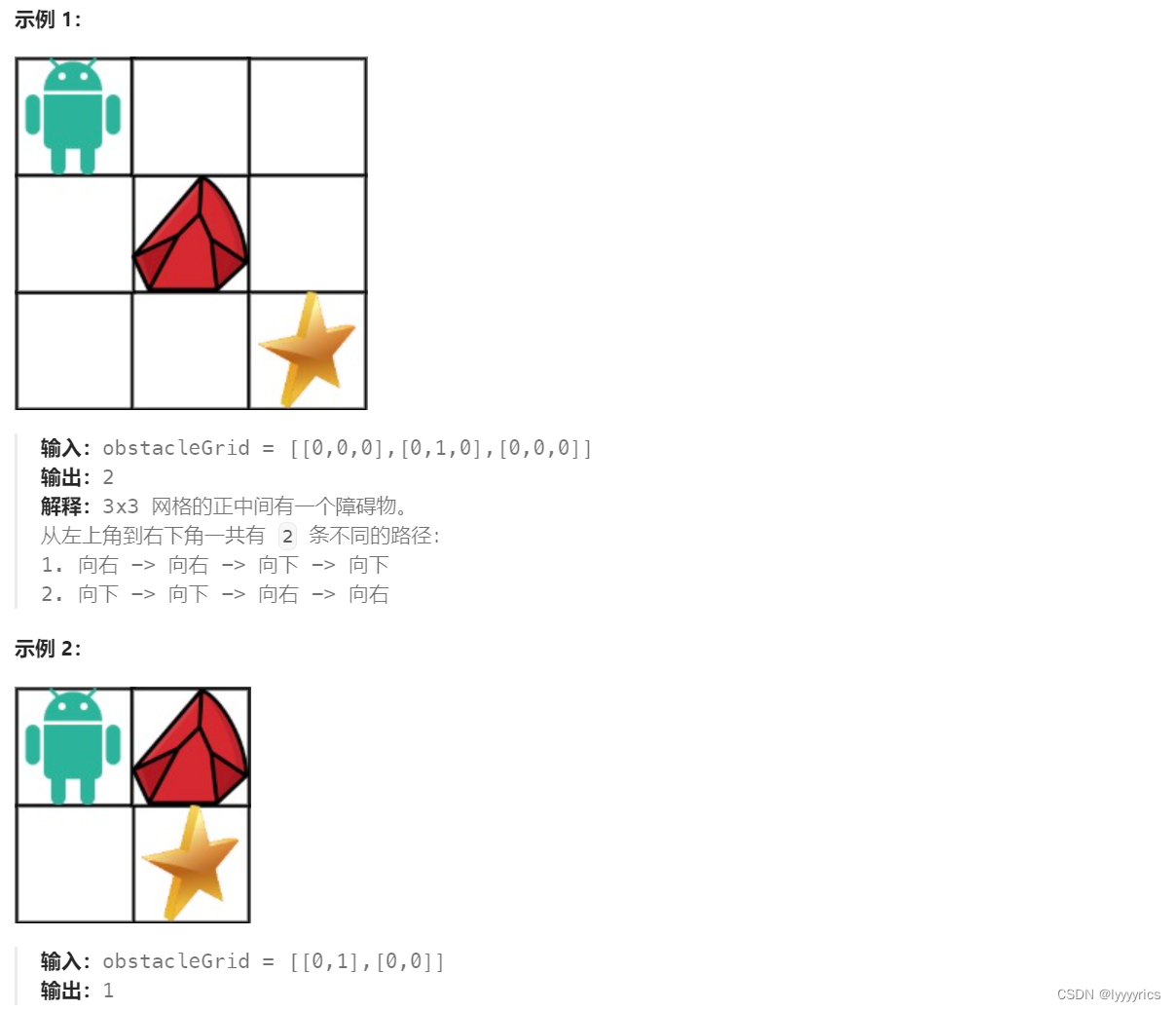
这道题和上一道题其实是一样的，只需要加一个判断，如果obstacleGrid数组中的值是1的话当前方法数就是0，所以在上道题的条件下加一个if条件的判断即可。
代码展示：

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m=obstacleGrid.size();
        int n=obstacleGrid[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,0));
        dp[0][1]=1;
        for(int i=1;i<m+1;i++)
        {
            for(int j=1;j<n+1;j++)
            {
                if(obstacleGrid[i-1][j-1]==0)
                {
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
                }
            }
        }
        return dp[m][n];
    }
};

运行结果：
在这里插入图片描述

3.下降路径最小和

题目链接
题目：

样例输出和输入：

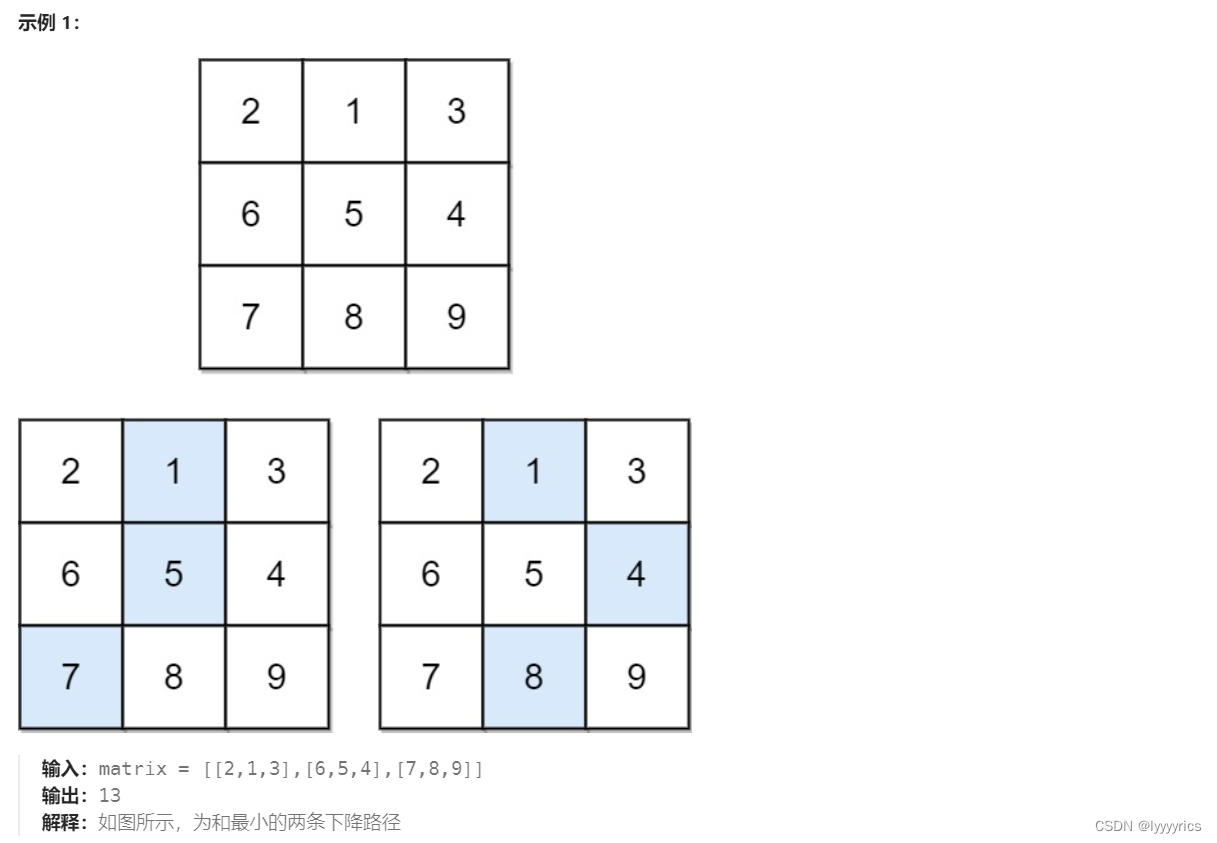
这道题的题意很简单，我们首先可以在一个n*n的矩阵的第一行选三个数
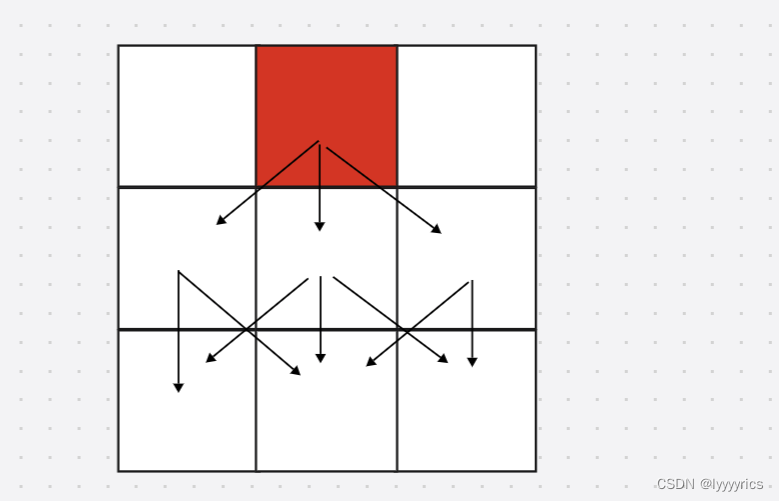
在这里插入图片描述
当我们选中间的格子时，可以下降的格子，我们假设当前格子的下标是[i,j]，则可以访问的下一行的下降的格子应该是：[i+1,j-1] [i+1,j] [i+1,j+1]这三个下标，这道题让我们求的就是到达最后一行的时候下降的最小的路径和，每个方格中的值就表示当前格子的路径数，所以当到达最后一行的时候走过的路径和就是走过的所有格子的值的和。
算法原理：
第一步：状态表示，这道题根据问题我们就知道这道题求的是下降路径最小和，所以我们的dp[i][j]表示的是到达[i][j]位置的时候的当前最小和。
第二步：状态转移方程，我们假设一个格子的下标是[i,j]。
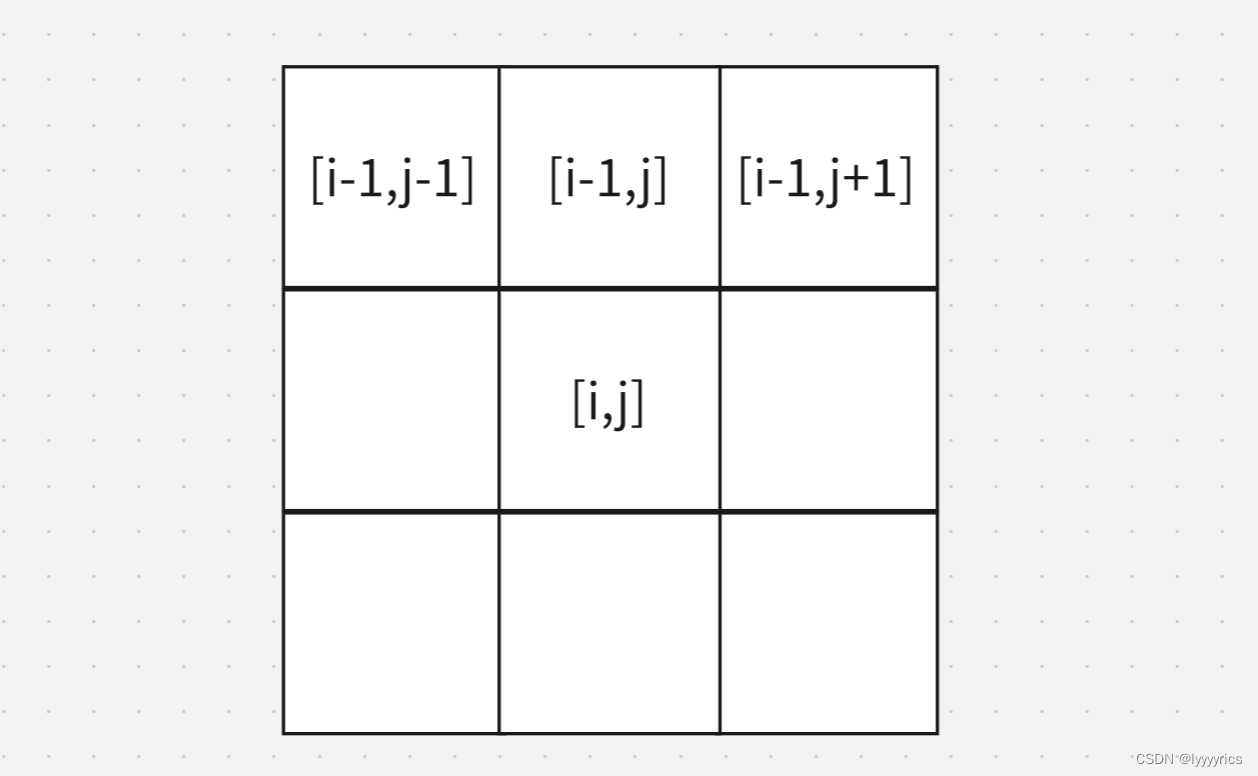
在这里插入图片描述

[i,j]的最小下降路径是不是应该等于上面三个的相邻的格子的最小路径加上当前格子的值。
所以状态转移方程应该是：dp[i][j]=min(dp[i-1][j],dp[i-1][j-1],dp[i-1][j+1])+matrix[i][j]
第三步：初始化为题，其实初始化还是和上面的一样，但是因为我们要用到上一行左边和右边的格子，所以这里会出现越界的格子不止左边和上面的格子还有右边的格子
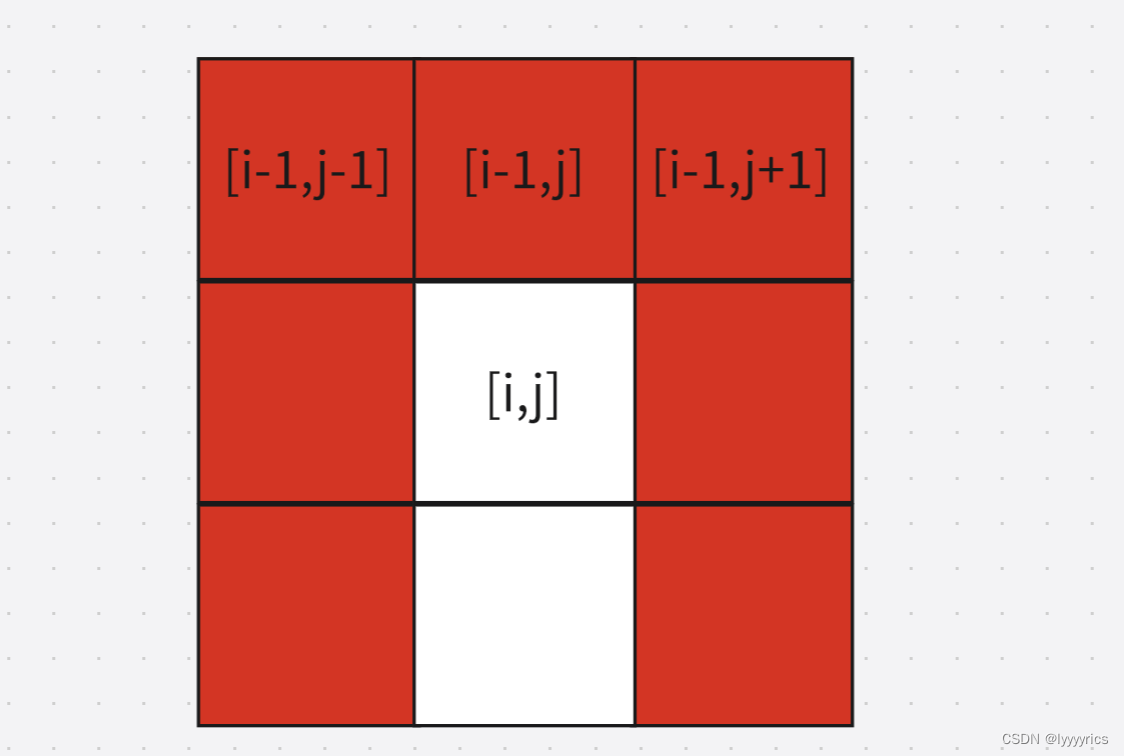
在这里插入图片描述
所以我们开辟空间应该这样开辟：

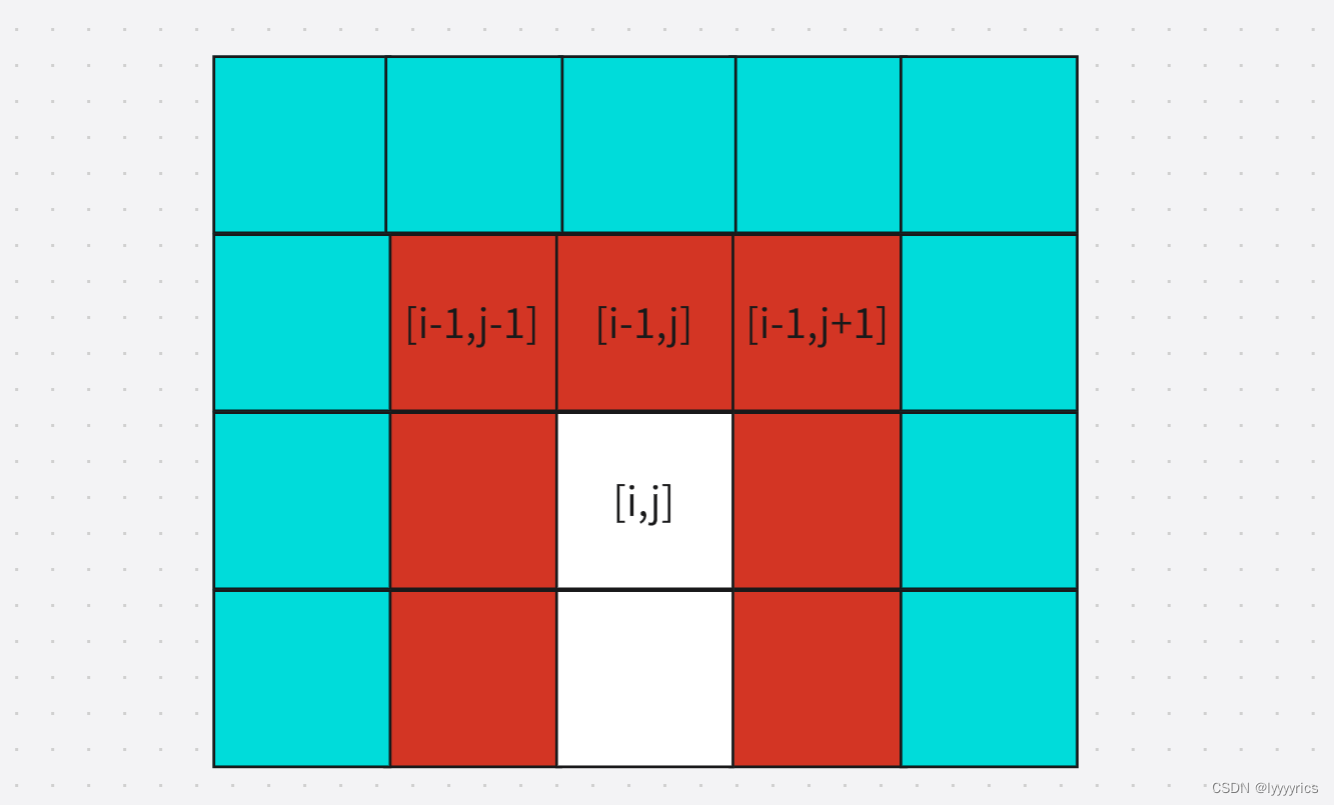
初始化应该初始化蓝色格子，由于当我们请求[i,j-1]位置的最小路径和的时候最左边的一列会影响最小值的大小，，所以这里初始化不能初始化为零，应该初始化为正无穷(INT_MAX)右边的蓝色格子也应该初始化为正无穷，但是上面一排的格子应该初始化为0，这样才不会影响结果。
第四步：填表顺序，填表顺序按顺序遍历。
第五步：返回值，由于这道题求的是最小路径和，所以应该返回dp数组中最后一行中的最小值。
代码展示：

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
        int m=matrix.size();
        int n=matrix[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+2,INT_MAX));
        for(int j=0;j<n+2;j++)
        {
            dp[0][j]=0;
        }
        for(int i=1;i<m+1;i++)
        {
            for(int j=1;j<n+1;j++)
            {
                dp[i][j]=min(min(dp[i-1][j-1],dp[i-1][j]),dp[i-1][j+1])+matrix[i-1][j-1];
            }
        }
        int Min=INT_MAX;
        for(int j=0;j<n+2;j++)
        {
            Min=min(Min,dp[m][j]);
        }
        return Min;
    }
};

运行结果：
在这里插入图片描述

4.珠宝的最高价值

题目链接
题目：

样例输出和输入：

这道题让我们求出珠宝的最高价值，
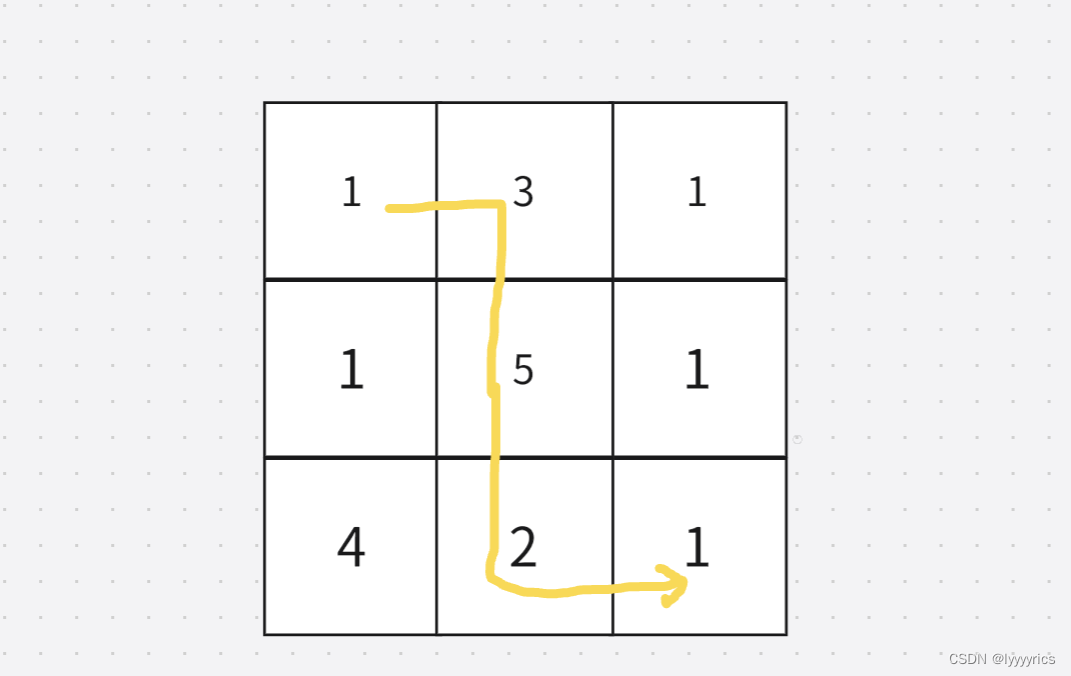
在这里插入图片描述
很显然根据示例一种的例子，价值最高的珠宝应该是这条路线之和，然后返回
算法原理：
状态表示：dp[i][j]当前位置的珠宝的最高价值。
状态转移方程：max(dp[i-1][j]+frame[i-1][j-1],dp[i][j-1]+frame[i-1][j-1])
初始化：初始化应该初始化最左边和最上面，初始化为零，因为当前的礼物价值是0.
代码展示：

class Solution {
public:
    int jewelleryValue(vector<vector<int>>& frame) {
        int m=frame.size();
        int n=frame[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,0));
        for(int i=1;i<m+1;i++)
        {
            for(int j=1;j<n+1;j++)
            {
                dp[i][j]=max(dp[i-1][j]+frame[i-1][j-1],dp[i][j-1]+frame[i-1][j-1]);
            }
        }
        return dp[m][n];
    }
};

运行结果：
在这里插入图片描述

5.地下城游戏

题目链接
题目：

样例输出和输入：

这道题让我们求出就出公主需要的最小健康值，当我们找到最小的一个路径的和加上1就是需要的最小的健康值。
算法原理：
状态表示：dp[i][j]表示当前位置救出公主需要的最小的健康程度，所以这道题的dp[i][j]应该是起点，而不是终点。
状态转移方程：我们设当前位置的最小的健康程度是dp[i][j]，则当我们用dp[i][j]-dungeon[i][j]>=dp[i+1][j],同理还有一种情况：dp[i][j]-dungeon[i][j]>=dp[i][j+1]所以最小的健康程度应该是求一个最小值，则状态转移方程：dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j]，但是需要注意的是如果dungeon是一个很大的正值的时候，会出现负数，由于这道题的题目要求是最低的健康值是1，到0或者小于零就死了，所以这道题不能出现负数，所以应该和1取一下max。
初始化，初始化我们和以前不一样，应该：
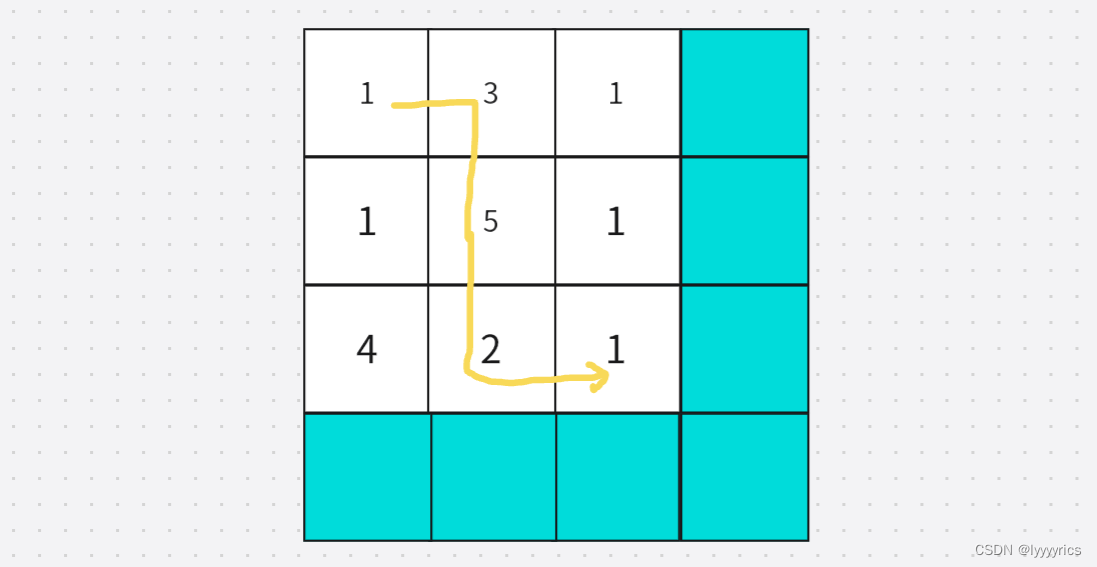
在这里插入图片描述
应该初始化左下角，由于取的最小值，所以不能初始化为0，应该初始化为INT_MAX，但是公主下面的和右边的格子应该初始化为1，因为救完公主的最小健康值是1，所以应该初始化为1.
填表顺序：从右下角倒着填表
返回值：返回dp数组的第一个值。
代码展示：

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) 
    {
        int m=dungeon.size();
        int n=dungeon[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));
        dp[m][n-1]=1;
        dp[m-1][n]=1;
        for(int i=m-1;i>=0;i--)
        {
            for(int j=n-1;j>=0;j--)
            {
                dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j];
                dp[i][j]=max(dp[i][j],1);
            }
        }
        return dp[0][0];
    }
};