文章目录
- week45 SAM优化器
- 摘要
- Abstract
- 1. 题目
- 2. Abstract
- 3. 锐度感知最小化
- 3.1 问题提出
- 3.2 方法提出
- 4. 文献解读
- 4.1 Introduction
- 4.2 创新点
- 4.3 实验过程
- 5. 结论
- 6.代码复现
- 小结
- 参考文献
week45 SAM优化器
摘要
本周阅读了题为Sharpness-Aware Minimization for Efficiently Improving Generalization的论文。为了将损失数据与泛化过程关联,引入了一种新颖算法“锐度感知最小化”(SAM),该程序能同时最小化损失值和损失锐度。实证结果表明,SAM提高了多个基准数据集和模型的泛化能力,且对标签噪声具有鲁棒性。本文在末尾部分简要介绍了SAM程序的核心代码,并给出了简洁的注释。
Abstract
This week’s weekly newspaper decodes the paper entitled Sharpness-Aware Minimization for Efficiently Improving Generalization. To associate loss data with the generalization process, a novel procedure called “Sharpness-Aware Minimization” (SAM) is introduced, which can minimize both loss value and loss sharpness. Empirical results show that SAM improves the generalization capabilities of multiple benchmark datasets and models, and it is robust to label noise. In the closing section of this article, we briefly introduce the core code of the SAM (Sharpness-Aware Minimization) procedure and provide concise comments for it.
1. 题目
标题:Sharpness-Aware Minimization for Efficiently Improving Generalization
作者:Pierre Foret, Ariel Kleiner, Hossein Mobahi, Behnam Neyshaburhttps://arxiv.org/search/cs?searchtype=author&query=Redko,+I)
发布:Published as a conference paper at ICLR 2021
链接:https://arxiv.org/abs/2010.01412
tip:上周的论文使用了该论文的锐度感知最小化技术,本周阅读该论文作为上周论文的补充
2. Abstract
为了将损失数据构成的图像与泛化过程联系起来,引入了一种新颖、有效的程序,可以同时最小化损失值和损失锐度。特别是,“锐度感知最小化”(SAM)算法寻找位于具有一致低损耗的邻域中的参数;该公式产生了最小最大优化问题,可以有效地执行梯度下降。该文提供的实证结果表明,SAM 改进了各种基准数据集(例如 CIFAR-{10, 100}、ImageNet、微调任务)和模型的模型泛化能力,为多个数据集带来了新颖的最先进性能。此外,该文发现 SAM 本身提供的标签噪声鲁棒性与专门针对噪声标签学习的最先进程序提供的鲁棒性相当。
To connect the image formed by loss data with the generalization process, a novel and effective procedure is introduced that can minimize both loss value and loss sharpness simultaneously. Specifically, the “Sharpness-Aware Minimization” (SAM) procedure seeks parameters located in a neighborhood with consistently low loss; this formula leads to a minimax optimization problem that can efficiently perform gradient descent. The empirical results provided in this paper show that SAM improves the model generalization capabilities for various benchmark datasets (such as CIFAR-{10, 100}, ImageNet, fine-tuning tasks), and models, bringing novel state-of-the-art performance for multiple datasets. In addition, the paper finds that the label noise robustness provided by SAM itself is comparable to that offered by state-of-the-art procedures specifically designed for noisy label learning.
3. 锐度感知最小化
综合了另一篇论文:ASAM: Adaptive Sharpness-Aware Minimization
for Scale-Invariant Learning of Deep Neural Networks 对理论部分的解释
该方法不是寻找简单地具有低训练损失值 L S ( w ) L_S(w) LS(w) 的参数值 w,而是寻找整个邻域都具有一致低训练的参数值损失值(相当于具有低损失和低曲率的邻域)
3.1 问题提出
- 目标函数:
L Q ( w ) L_{\mathscr Q}(w) LQ(w)式总体损失值,而训练集 L S ( w ) L_S(w) LS(w)表示样本损失值,即训练集S损失值$ \mathscr{D} ,使用 ,使用 ,使用L_S(w) 估计 估计 估计L_{\mathscr Q}(w)$
根据PAC-Bayesian generalization bound定理的非正式形式:对于任何
ρ
>
0
\rho>0
ρ>0(
ρ
\rho
ρ为领域大小),从分布来看,生成的训练集大概率满足:
L
D
(
w
)
≤
max
∣
∣
ϵ
∣
∣
2
≤
ρ
L
S
(
w
+
ϵ
)
+
h
(
∣
∣
w
∣
∣
2
2
/
ρ
2
)
L_\mathscr{D}(w)\leq\max_{||\epsilon||_2\leq \rho}L_S(w+\epsilon)+h(||w||^2_2/\rho^2)
LD(w)≤∣∣ϵ∣∣2≤ρmaxLS(w+ϵ)+h(∣∣w∣∣22/ρ2)
其中
h
:
R
+
→
R
+
h : \mathbb R^+ \rightarrow \mathbb R^+
h:R+→R+ 是严格递增函数,其具体形式如下
对于任何
ρ
>
0
ρ > 0
ρ>0 和任何分布
D
\mathscr D
D,选择训练集
S
∼
D
S \sim \mathscr D
S∼D 的概率为
1
−
δ
1 − δ
1−δ
L
D
(
w
)
≤
max
∣
∣
ϵ
∣
∣
2
≤
ρ
L
S
(
w
+
ϵ
)
+
k
log
(
1
+
∣
∣
w
∣
∣
2
2
ρ
2
(
1
+
log
(
n
)
k
)
2
)
+
4
log
n
δ
+
O
~
(
1
)
n
−
1
L_\mathscr D(w)\leq \max_{||\epsilon||_2\leq \rho}L_S(w+\epsilon)+\sqrt{\frac{k\log(1+\frac{||w||^2_2}{\rho^2}(1+\sqrt{\frac{\log(n)}{k}})^2)+4\log\frac{n}{\delta}+\tilde O(1)}{n-1}}
LD(w)≤∣∣ϵ∣∣2≤ρmaxLS(w+ϵ)+n−1klog(1+ρ2∣∣w∣∣22(1+klog(n))2)+4logδn+O~(1)
其中
n
=
∣
S
∣
n = |S|
n=∣S∣,k是参数数量,假设
L
D
(
w
)
≤
E
ϵ
i
∼
N
(
0
,
ρ
)
[
L
D
(
w
+
ϵ
)
]
L_\mathscr D(w) ≤ E{\epsilon_i\sim \mathcal N(0,\rho)}[L_\mathscr D(w + \epsilon)]
LD(w)≤Eϵi∼N(0,ρ)[LD(w+ϵ)]。假设条件意味着添加高斯扰动不应降低测试误差。
为了得到损失函数 L Q L_\mathscr Q LQ的极小解,现求不等式右侧 max ∣ ∣ ϵ ∣ ∣ 2 ≤ ρ L S ( w + ϵ ) + h ( ∣ ∣ w ∣ ∣ 2 2 / ρ 2 ) \max_{||\epsilon||_2\leq \rho}L_S(w+\epsilon)+h(||w||^2_2/\rho^2) max∣∣ϵ∣∣2≤ρLS(w+ϵ)+h(∣∣w∣∣22/ρ2)的最小值
- 锐度概念
将不等式右侧展开为如下形式
[
max
∣
∣
ϵ
∣
∣
2
≤
ρ
L
S
(
w
+
ϵ
)
−
L
S
(
w
)
]
+
L
S
(
w
)
+
h
(
∣
∣
w
∣
∣
2
2
/
ρ
2
)
[\max_{||\epsilon||_2\leq \rho}L_S(w+\epsilon)-L_S(w)]+L_S(w)+h(||w||^2_2/\rho^2)
[∣∣ϵ∣∣2≤ρmaxLS(w+ϵ)−LS(w)]+LS(w)+h(∣∣w∣∣22/ρ2)
中括号中即
L
S
L_S
LS锐度,其可以衡量从
w
\boldsymbol{w}
w移动到相临近的参数值,training loss增加的速度。从而上式可以理解为
s
h
a
r
p
n
e
s
s
+
t
r
a
i
n
i
n
g
l
o
s
s
+
w
sharpness+training\ loss+w
sharpness+training loss+w的正则项
- 进一步变换
将w的正则项使用L2正则项
L2正则项(Ridge):L2正则项将模型参数的平方和作为正则化项,即 L 2 = λ ∑ i = 1 n ( w i 2 ) L2=λ \sum^n_{i=1}(w_i^2) L2=λ∑i=1n(wi2)。它可以防止模型中的参数过大,从而减少模型的过拟合。
将
h
(
∣
∣
w
∣
∣
2
2
/
ρ
2
)
h(||w||^2_2/\rho^2)
h(∣∣w∣∣22/ρ2)替换为
λ
∣
∣
w
∣
∣
2
2
\lambda||w||^2_2
λ∣∣w∣∣22,
λ
\lambda
λ为参数衰减
min
w
L
S
S
A
M
(
w
)
+
λ
∣
∣
w
∣
∣
2
2
where
L
S
S
A
M
(
w
)
≜
max
∣
∣
ϵ
∣
∣
p
≤
ρ
L
S
(
w
+
ϵ
)
\min_wL^{SAM}_S(w)+\lambda||w||^2_2\ \text{where}\ L^{SAM}_S(w)\triangleq \max_{||\epsilon||_p\leq\rho}L_S(w+\epsilon)
wminLSSAM(w)+λ∣∣w∣∣22 where LSSAM(w)≜∣∣ϵ∣∣p≤ρmaxLS(w+ϵ)
其中
ρ
≥
0
\rho\geq 0
ρ≥0为一个超参,
p
∈
[
1
,
∞
]
p\in [1,\infin]
p∈[1,∞],文中给出p=2为最优
3.2 方法提出
为了最小化
L
S
S
A
M
(
w
)
L^{SAM}_S (w)
LSSAM(w),通过内部最大化求导,得到了
∇
w
L
S
S
A
M
(
w
)
\nabla_wL^{SAM}_S(w)
∇wLSSAM(w)的高效且有效的近似,这反过来又能够将随机梯度下降直接应用于 SAM 目标。沿着这条路径前进,首先通过
L
S
(
w
+
ϵ
)
L_S(w + \epsilon)
LS(w+ϵ)的一阶泰勒展开来近似内部最大化问题,其在0附近,如下
ϵ
∗
(
w
)
≜
argmax
∣
∣
ϵ
∣
∣
p
≤
ρ
L
S
(
w
+
ϵ
)
≈
argmax
∣
∣
ϵ
∣
∣
p
≤
ρ
L
S
(
w
)
+
ϵ
T
∇
w
L
S
(
w
)
=
argmax
∣
∣
ϵ
∣
∣
p
≤
ρ
ϵ
T
∇
w
L
S
(
w
)
\begin{align*} \epsilon^*(w)&\triangleq\text{argmax}_{||\epsilon||_p\leq\rho}L_S(w+\epsilon)\\ &\approx\text{argmax}_{||\epsilon||_p\leq\rho}L_S(w)+\epsilon^T\nabla_wL_S(w)\\ &=\text{argmax}_{||\epsilon||_p\leq \rho}\epsilon^T\nabla_wL_S(w) \end{align*}
ϵ∗(w)≜argmax∣∣ϵ∣∣p≤ρLS(w+ϵ)≈argmax∣∣ϵ∣∣p≤ρLS(w)+ϵT∇wLS(w)=argmax∣∣ϵ∣∣p≤ρϵT∇wLS(w)
inner maximization,简而言之,在训练集上更新模型超参数使得损失函数值最大,得到当前最优模型参数的问题,即求一个超参使得损失函数最大化
上式根据在 x = w + ϵ x=w+\epsilon x=w+ϵ处, ϵ → 0 \epsilon\rightarrow0 ϵ→0一阶泰勒展开式以及 argmax ∣ ∣ ϵ ∣ ∣ p ≤ ρ L S ( w ) = 0 \text{argmax}_{||\epsilon||_p\leq\rho}L_S(w)=0 argmax∣∣ϵ∣∣p≤ρLS(w)=0
用
ϵ
^
(
w
)
\hat \epsilon(w)
ϵ^(w)表示
ϵ
(
w
)
\epsilon(w)
ϵ(w)由经典对偶范数问题的解给出:
ϵ
^
(
w
)
=
ρ
sign
(
∇
w
L
S
(
w
)
)
∣
∇
w
L
S
(
w
)
∣
q
−
1
/
(
∣
∣
∇
w
L
S
(
w
)
∣
∣
q
q
)
1
/
p
(2)
\hat \epsilon(w)=\rho\ \text{sign}(\nabla_wL_S(w))|\nabla_wL_S(w)|^{q-1}/(||\nabla_wL_S(w)||^q_q)^{1/p}\tag{2}
ϵ^(w)=ρ sign(∇wLS(w))∣∇wLS(w)∣q−1/(∣∣∇wLS(w)∣∣qq)1/p(2)
其中
1
/
p
+
1
/
q
=
1
1/p+1/q=1
1/p+1/q=1
将p=2带入上式有
ϵ
^
(
w
)
=
ρ
sign
(
∇
w
L
S
(
w
)
)
∣
∇
w
L
S
(
w
)
∣
∣
∣
∇
w
L
S
(
w
)
∣
∣
2
=
ρ
∇
L
S
(
w
)
∣
∣
∇
L
S
(
w
)
∣
∣
2
\begin{align*} \hat \epsilon(w)&=\rho\ \text{sign}(\nabla_wL_S(w))\frac{|\nabla_wL_S(w)|}{||\nabla_wL_S(w)||_2}\\ &=\rho \frac{\nabla L_S(w)}{||\nabla L_S(w)||_2} \end{align*}
ϵ^(w)=ρ sign(∇wLS(w))∣∣∇wLS(w)∣∣2∣∇wLS(w)∣=ρ∣∣∇LS(w)∣∣2∇LS(w)
根据上式对于
∇
w
L
S
S
A
M
(
w
)
\nabla_wL_S^{SAM}(w)
∇wLSSAM(w)有:
∇
w
L
S
S
A
M
(
w
)
≈
∇
w
L
S
(
w
+
ϵ
^
(
w
)
)
=
d
(
w
+
ϵ
^
(
w
)
)
d
w
∇
w
L
S
(
w
)
∣
w
+
ϵ
^
(
w
)
=
∇
w
L
S
(
w
)
∣
w
+
ϵ
^
(
w
)
+
d
ϵ
^
(
w
)
d
w
∇
w
L
S
(
w
)
∣
w
+
ϵ
^
(
w
)
\begin{align*} \nabla_wL_S^{SAM}(w)&\approx \nabla_wL_S(w+\hat \epsilon(w))\\ &=\frac{\text{d}(w+\hat \epsilon(w))}{\text{d}w}\nabla_wL_S(w)|_{w+\hat \epsilon(w)}\\ &=\nabla_wL_S(w)|_{w+\hat \epsilon(w)}+\frac{\text{d}\hat \epsilon(w)}{\text{d}w}\nabla_wL_S(w)|_{w+\hat \epsilon(w)} \end{align*}
∇wLSSAM(w)≈∇wLS(w+ϵ^(w))=dwd(w+ϵ^(w))∇wLS(w)∣w+ϵ^(w)=∇wLS(w)∣w+ϵ^(w)+dwdϵ^(w)∇wLS(w)∣w+ϵ^(w)
上式使用了复合微分
d
f
(
g
(
x
)
)
d
x
=
d
g
(
x
)
d
x
d
f
(
x
)
∣
g
(
x
)
\frac{df(g(x))}{dx}=\frac{dg(x)}{dx}df(x)|_{g(x)}
dxdf(g(x))=dxdg(x)df(x)∣g(x)
文中在附录C.4部分指出上式中二阶项会大幅降低性能,因此仅保留第一项有
∇
w
L
S
S
A
M
(
w
)
≈
∇
w
L
S
(
w
)
∣
w
+
ϵ
^
(
w
)
(3)
\nabla_wL^{SAM}_S(w)\approx\nabla_wL_S(w)|_{w+\hat\epsilon(w)}\tag{3}
∇wLSSAM(w)≈∇wLS(w)∣w+ϵ^(w)(3)
将一般的优化器应用于SAM目标函数
L
S
S
A
M
(
w
)
L^{SAM}_S(w)
LSSAM(w),并使用上式计算目标函数的梯度,最终有SAM算法
综上,SAM算法如下


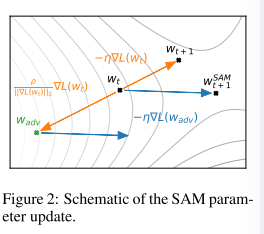
图 2 示意性地说明了单个 SAM 参数更新。
4. 文献解读
4.1 Introduction

上图为图一,左侧:改用 SAM 后错误率降低。每个点都是不同的数据集/模型/数据增强。 中间:使用 SGD 训练的 ResNet 收敛到的急剧最小值。 右侧:使用 SAM 训练的相同 ResNet 收敛到的宽最小值。
损失图像的几何形状(特别是最小值的平坦度)与泛化之间的联系已从理论和实证角度进行了广泛的研究。虽然这种联系有望实现新的模型训练方法,从而产生更好的泛化能力,但迄今为止,专门寻找更平坦的最小值并进一步有效提高一系列最先进模型泛化能力的实用高效算法仍然难以实现。
该文提出了一种新的高效、可扩展且有效的方法来提高模型泛化能力,该方法直接利用损失图像的几何形状及其与泛化的联系,并且是对现有技术的有力补充。
4.2 创新点
该问题提出了SAM算法,主要贡献大致如下:
- 引入了锐度感知最小化(SAM),这是一种通过同时最小化损失值和损失锐度来提高模型泛化能力的新颖过程。 SAM 通过寻找位于具有一致低损失值的邻域中的参数(而不是仅本身具有低损失值的参数,如图 1 的中图和右图所示)来发挥作用,并且可以高效且轻松地实现。
- 通过严格的实证研究表明,使用 SAM 可以提高一系列广泛研究的计算机视觉任务(例如 CIFAR-{10, 100}、ImageNet、微调任务)和模型的模型泛化能力,如图1左图所示。例如,应用 SAM 为许多已经深入研究的任务带来了新颖的最先进的性能,例如 ImageNet、CIFAR-{10, 100}、SVHN、Fashion-MNIST 以及标准集图像分类微调任务(例如,Flowers、Stanford Cars、Oxford Pets 等)。
- 研究表明,SAM 还提供了与专门针对噪声标签学习的最先进程序所提供的鲁棒性来处理标签噪声。
- 通过SAM 提供的镜头,通过提出一个有前途的新锐度概念(我们称之为m-锐度),进一步阐明了损失锐度和泛化之间的联系。
4.3 实验过程
为了评估 SAM 的功效,将其应用于一系列不同的任务,包括从头开始进行图像分类(包括在 CIFAR-10、CIFAR-100 和 ImageNet 上)、微调预训练模型以及使用噪声标签进行学习。在所有情况下,通过简单地用 SAM 替换用于训练现有模型的优化过程,并计算对模型泛化的影响来衡量使用 SAM 的好处。如下所示,在绝大多数情况下,SAM 显着提高了泛化性能。
CIFAR-10和CIFAR-100
以下模型未经预训练,使用具有 Shake-Shake正则化的 WideResNets和具有 ShakeDrop 正则化的 PyramidNet,模型经过调整,其中包括仔细选择的正则化方案以防止过度拟合,故主要从提高泛化能力方面进行提升。
所有结果都使用基本数据增强(水平翻转、四个像素填充和随机裁剪)。还评估了更先进的数据增强方法,例如剪切正则化和 AutoAugment
SAM 有一个超参数 ρ(邻域大小),我们使用 10% 的训练集作为验证集,通过 {0.01, 0.02, 0.05, 0.1, 0.2, 0.5} 上的网格搜索进行调整。允许每个非 SAM 训练运行执行的次数是每个 SAM 训练运行的两倍,并且报告每次非 SAM 训练在标准历元计数或双倍历元计数中运行所获得的最佳分数。
对报告结果的每个实验条件运行五个独立的副本(每个副本都具有独立的权重初始化和数据改组),报告测试集上产生的平均误差(或准确性)以及相关的 95% 置信区间。实现利用 JAX,并且在具有 8 个 NVidia V100 GPU 的单个主机上训练所有模型。为了计算跨多个加速器并行时的 SAM 更新,在加速器之间均匀划分每个数据批次,独立计算每个加速器上的 SAM 梯度,并对所得的子批次 SAM 梯度进行平均以获得最终的 SAM 更新。
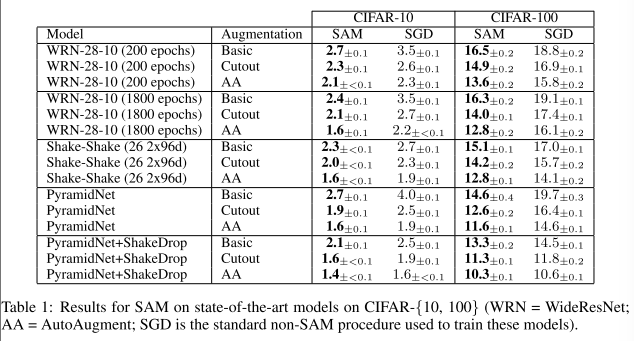
如表 1 所示,SAM 提高了针对 CIFAR-10 和 CIFAR-100 评估的所有设置的泛化能力。例如,SAM 使简单的 WideResNet 能够实现 1.6% 的测试误差,而没有 SAM 时误差为 2.2%。以前只能通过使用更复杂的模型架构(例如 PyramidNet)和正则化方案(例如 Shake-Shake、ShakeDrop)才能实现这种收益; SAM 提供了一种易于实施、独立于模型的替代方案。此外,即使应用于已经使用复杂正则化的复杂架构,SAM 也能带来改进:例如,将 SAM 应用于具有 ShakeDrop 正则化的 PyramidNet,会在 CIFAR-100 上产生 10.3% 的错误,这是一个新的状态在不使用额外数据的情况下,该数据集上的最新技术。
SVHN和 Fashion-MNIST 数据集
SAM 再次使简单的 WideResNet 能够达到或高于这些数据集最先进水平的精度:SVHN 的误差为 0.99%,Fashion-MNIST 的误差为 3.59%。
ResNets trained on ImageNet
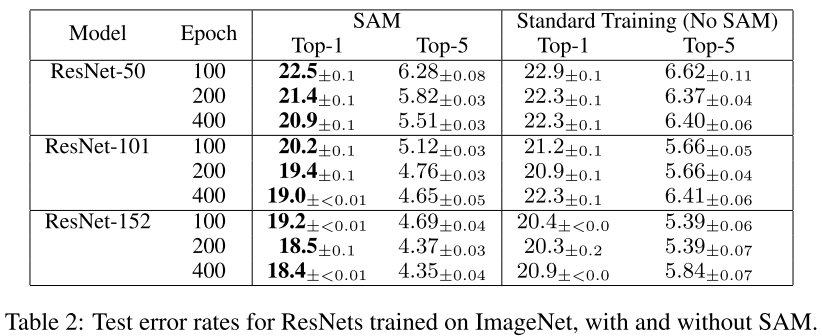
如表 2 所示,SAM 再次持续提高性能,例如将 ResNet-152 的 ImageNet top-1 错误率从 20.3% 提高到 18.4%。此外,请注意,SAM 可以增加训练时期的数量,同时继续提高准确性而不会过度拟合。相比之下,当训练从 200 epoch 扩展到 400 epoch 时,标准训练程序(没有 SAM)通常会显着过度拟合。
5. 结论
在这项工作中,引入了 SAM,这是一种新颖的算法,通过同时最小化损失值和损失锐度来提高泛化能力;通过严格的大规模实证评估证明了 SAM 的功效。在理论方面,m-锐度产生的每个数据点锐度的概念(与过去通常研究的在整个训练集上计算的全局锐度相反)提出了一个有趣的新镜头来研究概括。从方法论上来说,结果表明,SAM 有可能在目前依赖 Mixup 的鲁棒或半监督方法中用来代替 Mixup(例如,MentorSAM)。
6.代码复现
该代码可从 https://github.com/romilbert/samformer 获取。
SAM
这段代码定义了一个名为 SAM 的 Python 类,它是一个用于优化神经网络训练的自定义优化器,继承自 PyTorch 的 Optimizer。SAM 代表 Sharpness-Aware Minimization,这是一种用于改进模型泛化能力的优化技术,通过最小化损失函数的锐度来实现。
import torch
from torch.optim import Optimizer
class SAM(Optimizer):
"""
SAM: Sharpness-Aware Minimization for Efficiently Improving Generalization https://arxiv.org/abs/2010.01412
https://github.com/davda54/sam
"""
def __init__(self, params, base_optimizer, rho=0.05, adaptive=False, **kwargs):
assert rho >= 0.0, f"Invalid rho, should be non-negative: {rho}"
defaults = dict(rho=rho, adaptive=adaptive, **kwargs)
super(SAM, self).__init__(params, defaults)
self.base_optimizer = base_optimizer(self.param_groups, **kwargs)
self.param_groups = self.base_optimizer.param_groups
@torch.no_grad()
def first_step(self, zero_grad=False):
grad_norm = self._grad_norm()
for group in self.param_groups:
scale = group["rho"] / (grad_norm + 1e-12)
for p in group["params"]:
if p.grad is None:
continue
e_w = (
(torch.pow(p, 2) if group["adaptive"] else 1.0)
* p.grad
* scale.to(p)
)
p.add_(e_w) # climb to the local maximum "w + e(w)"
self.state[p]["e_w"] = e_w
if zero_grad:
self.zero_grad()
@torch.no_grad()
def second_step(self, zero_grad=False):
for group in self.param_groups:
for p in group["params"]:
if p.grad is None:
continue
p.sub_(self.state[p]["e_w"]) # get back to "w" from "w + e(w)"
self.base_optimizer.step() # do the actual "sharpness-aware" update
if zero_grad:
self.zero_grad()
@torch.no_grad()
def step(self, closure=None):
assert (
closure is not None
), "Sharpness Aware Minimization requires closure, but it was not provided"
closure = torch.enable_grad()(
closure
) # the closure should do a full forward-backward pass
self.first_step(zero_grad=True)
closure()
self.second_step()
def _grad_norm(self):
shared_device = self.param_groups[0]["params"][
0
].device # put everything on the same device, in case of model parallelism
norm = torch.norm(
torch.stack(
[
((torch.abs(p) if group["adaptive"] else 1.0) * p.grad)
.norm(p=2)
.to(shared_device)
for group in self.param_groups
for p in group["params"]
if p.grad is not None
]
),
p=2,
)
return norm
以上为torch中实现SAM优化器的方法,以下介绍该论文所构建的SAM优化器,代码从https://github.com/google-research/sam获取,但该部分代码使用tensorflow实现。
若要在编程中使用SAM优化器,需要引用sam包,其大致相关配置为numpy-1.23.5 sam-3.1.11 scikit-learn-1.2.2
此外,若要使用pytorch实现的训练代码,可以参考https://blog.csdn.net/weixin_44649780/article/details/124535616
小结
在这项工作中,引入了 SAM,这是一种新颖的算法,通过同时最小化损失值和损失锐度来提高泛化能力;通过严格的大规模实证评估证明了 SAM 的功效。在理论方面,m-锐度产生的每个数据点锐度的概念(与过去通常研究的在整个训练集上计算的全局锐度相反)提出了一个有趣的新镜头来研究概括。从方法论上来说,结果表明,SAM 有可能在目前依赖 Mixup 的鲁棒或半监督方法中用来代替 Mixup(例如,MentorSAM)。
参考文献
[1] Pierre Foret, Ariel Kleiner, Hossein Mobahi, Behnam Neyshabur “Sharpness-Aware Minimization for Efficiently Improving Generalization” [C], ICLR 2021