PDF文档公众号回复关键字:20240629

2022 CSP-J 选择题
单项选择题(共15题,每题2分,共计30分:每题有且仅有一个正确选项)
5.对于入栈顺序为a,b,c,d,e的序列,下列( )不合法的出栈序列
A. a,b,c,d,e
B. e,d,c,b,a
C. b,a,c,d,e
D. c,d,a,e,b
8.如果一颗二叉树只有根节点,那么这棵二叉树高度为1。请问高度为5的完全二叉树有( )种不同的形态
A. 16
B. 15
C. 17
D. 32
9.表达式a* (b+c)* d的后缀表达式为( ),其中 *和 +是运算符
A. * * a + b c d
B. a b c + * d *
C. a b c + d * *
D. * a * + b c d
11.在数据压缩编码中的哈夫曼编码方法,在本质上是一种( ) 策略
A. 枚举
B. 贪心
C. 递归
D. 动态规划
15.有四个人要从A点坐一条船过河到B点,船一开始在A点。该船一次最多可坐两个人。已知这四个人中每个人独自坐船的过河时间分别为1、2、4、8,且两个人坐船的过河时间为两人独自过河时间的较大者。则最短( )时间可以让四个人都过河到B点(包括从B点把船开回A点的时间)
A. 14
B. 15
C. 16
D. 17
2 相关知识点
栈
栈又名堆栈,是一种限定仅在表尾进行插入和删除操作的线性表,这一端称为栈顶,另一端称为栈底
栈中的数据元素遵守后进先出的原则

二叉树
每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点),并且,二叉树的子树有左右之分,其次序不能任意颠倒,例如下面是一棵二叉树

满二叉树
满二叉树又叫完美二叉树,除了叶子结点之外的每一个结点都有两个孩子,树的叶子节点均在最后一层(也就是形成了一个完美的三角形)

完全二叉树
除了最下层,其他每层都饱满,去除最后一层是一棵满二叉树,最下层的结点都集中在该层最左边的若干位置上

前缀表达式
前缀表达式,也称为波兰表达式,是一种算术表达式表示方法,其中运算符位于操作数之前.
//示例1 中缀表达式a+b对应的前缀表达式
+a bC++
//示例2 中缀表达式3+4*2对应的前缀表达式
+ 3 * 4 2
中缀表达式
是一种常见的算术表达式表示方法,其中运算符位于操作数之间
//示例1
3 + 4 * 2
//示例2
(1 + 2) * (3 - 4)C++
后缀表达式
后缀表达式,也称为逆波兰表达式,是一种算术表达式表示方法,其中运算符位于操作数之后
//示例1 中缀表达式a+b对应的后缀表达式C++
a b+
//示例2 中缀表达式3+4*2对应的前缀表达式
3 4 2 * +
中缀表达式转后缀表达式
确定优先级,按优先级逐一处理操作符(把操作符从操作数中间移到操作数后边)
例如如下中缀表达式转为后缀表达式
1 + ( 2 + 3)* 4 ) – 5
// 按优先级对表达式数字加括号
((1 + (( 2 + 3)* 4 )) – 5 )
//从最里面的一层括号开始运算,转换成后缀表达式
//转换方法,去除括号,数字在前,顺序不变,操作符移到最后
1. ( 2 + 3) => 2 3 +
// ( 2 + 3)可以看作一个整体x
2. (( 2 + 3)* 4 ) => (x+4) => x 4 + => 2 3 + 4 *
//(( 2 + 3)* 4 )看作一个整体x
3. (1 + (( 2 + 3)* 4 ))=> (1+x)=>1 x + = 1 2 3 + 4 * +
// (1 + (( 2 + 3)* 4 )) 看作一个整体x
4. ((1 + (( 2 + 3)* 4 )) – 5 ) =>(x-5)=>x 5 - => 1 2 3 + 4 * + 5 -
所以转换后的后缀表达式为 1 2 3 + 4 * + 5 -
哈夫曼树
1 选剩下的两棵根权值最小的树合并成一棵新树
2 新树的根权值等于两棵合并前树的根权值和
3 重复1和2
哈夫曼编码
哈夫曼树的左右孩子进行编码称为哈夫曼编码,通常左边为0,右边为1
只对叶子节点进行编码/解码,编码唯一
哈夫曼编码是前缀编码,任何一个字符的编码都不是另一个字符编码的前缀(只有叶子节点编码)
哈夫曼编码左边为0,右边为1是通常规定,也可以左边为1右边为0,但确定后编码是唯一的
如果下图为字母a,b,c,d,e的编码,字母旁边对应数字为其出现的频率

贪心算法
所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择 。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的 局部最优解
哈夫曼编码总是把出现频率少的编码相对较长,从而保证全局总的编码最短
哈夫曼编码使用的是贪心算法进行编码
3 思路分析
5.对于入栈顺序为a,b,c,d,e的序列,下列( D )不合法的出栈序列
A. a,b,c,d,e
B. e,d,c,b,a
C. b,a,c,d,e
D. c,d,a,e,b
分析
根据入栈出栈性质模拟,栈为后进先出
A a 进 a 出 b 进 b 出 c 进 c 出 d 进 d 出 e 进 e 出 出栈顺序合法
B a 进 b 进 c 进 d 进 e 进 e 出 d 出 c 出 b 出 a 出 出栈顺序合法
C a 进 b 进 b 出 a 出 c 进 c 出 d 进 d 出 e 进 e 出 出栈顺序合法
D a 进 b 进 c 进 c 出 d 进 d 出 此时b在栈顶,a无法出栈
所以选 D
8.如果一颗二叉树只有根节点,那么这棵二叉树高度为1。请问高度为5的完全二叉树有( A )种不同的形态
A. 16
B. 15
C. 17
D. 32
分析
完全二叉树,除最后一层,其他层都是满的
高度为5有4层是满的,后面1层节点是前面节点的2倍(1个父节点都有2个子节点)
前4层是满的,形态不会变化,只有第5层形态可能变化,第5层节点只要保证从左到右排即可
具体如下
满二叉树
高度为1 1个节点 2^1-1=1
高度为2 1+2 个节点 2^2-1=3
高度为3 1+2+4个节点 2^3-1=7
高度为4 1+2+4+8 个节点2^4-1=15
高度为5 1+2+4+8+16 个节点 2^5-1=31
由于是完全二叉树,说明第5层必有节点,第5层的节点最多可以31-15=16个
当第5层节点为16个时,此时是5层的满二叉树,是特殊的完全二叉树
因此有16种不同的形态
9.表达式a* (b+c)* d的后缀表达式为( B ),其中 *和 +是运算符
A. * * a + b c d
B. a b c + * d *
C. a b c + d * *
D. * a * + b c d
分析
确定优先级,按优先级逐一处理操作符(把操作符从操作数中间移到操作数后边)
a * (b+c)* d -- ((a * (b+c))* d)
((a * (b+c))* d)
1 (b+c) => b c+
// (b+c) 可以看作一个整体x
(a * (b+c)) => (a * x) => a x * => a b c + *
//(a * (b+c)) 可以看作一个整体x
((a * (b+c))* d) => (x * d) => x d * => a b c + * d *
11.在数据压缩编码中的哈夫曼编码方法,在本质上是一种( B ) 策略
A. 枚举
B. 贪心
C. 递归
D. 动态规划
分析
哈夫曼编码总是把出现频率少的编码相对较长,从而保证全局总的编码最短
哈夫曼编码使用的是贪心算法进行编码

15.有四个人要从A点坐一条船过河到B点,船一开始在A点。该船一次最多可坐两个人。已知这四个人中每个人独自坐船的过河时间分别为1、2、4、8,且两个人坐船的过河时间为两人独自过河时间的较大者。则最短( B )时间可以让四个人都过河到B点(包括从B点把船开回A点的时间)
A. 14
B. 15
C. 16
D. 17
分析
贪心算法解决此问题,贪心策略
1从剩余的人中选择用时最小的2人过河
2 用时最小的人返回去接剩余的人
1 初始 1 2 4 8 在河的A边

2从剩余的 1 2 4 8 找用时最少的2人(1 和 2)过河到B ,用时为2

3 在B端选择用时间最少的去接,1去接,用时1

4 从剩余的 4 8 找用时最少的2人(4 和 8)过河到B ,用时为8

5 在B端选择用时间最少的去接,2去接,用时2

6 从剩余的 1 2 过河 用时为2
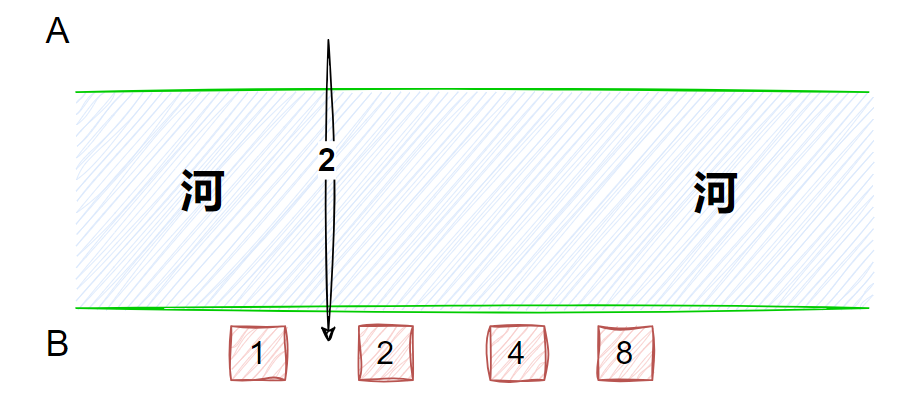
上述过河时间累加 2+1+8+2+2=15