前言
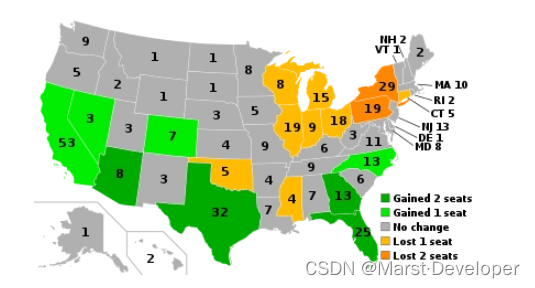
20世纪初,美国人口普查局局长约瑟夫·A·亨廷顿(Joseph A. Hill)和数学家爱德华·V·亨廷顿(Edward V. Huntington)在研究议会议席分配问题时,提出了一种基于数学原理的算法。该算法通过计算每个州的人口比例,来确定每个州应该分配的议会议席数量。
目录
算法来源
算法特点
算法步骤
应用场景
算法复杂度
代码
总结
算法来源
美国国会分配算法的历史发展可以追溯到美国建国初期。以下是其历史发展的简要概述
- 建国初期 美国国会的前身是1774年召开的第一届大陆会议。在1787年制定的美国宪法中,规定了国会由参议院和众议院组成,众议院议员根据各州人口比例分配,参议院议员则每州两名。
- 19世纪 19世纪中叶,美国国会通过了一系列法律和修正案,对国会席位的分配进行了调整。例如,1842年的国会立法规定各州必须按照人口比例划分选区,每个选区选举一名议员。
- 20世纪 20世纪初,随着美国人口的增长和变化,国会席位的分配再次成为争议焦点。1929年,美国国会通过了《众议院席位重新分配法案》,对众议院席位进行了重新分配。此后,国会席位的分配基本保持稳定,但随着时间的推移,一些州的人口增长或减少,导致其在国会中的代表权发生变化。
- 21世纪 21世纪以来,美国国会的分配算法仍然面临一些挑战和争议。例如,一些人认为当前的算法可能导致某些州在国会中的代表权不足,或者某些选区的划分不合理。此外,随着科技的发展和数据分析的应用,一些人也提出了使用更科学的方法来分配国会席位的建议。
算法特点
- 基于人口比例:根据各州人口数量的比例来分配议会议席。
- 考虑人口增长:在分配议会议席时,会考虑各州人口的增长情况。
- 数学原理:运用了数学方法和原理进行计算。
- 相对公平:旨在实现议会议席分配的相对公平性。
- 可操作性:具有一定的可操作性和实用性。
- 适应性:能够适应不同的人口变化和政治情况。
算法步骤
1.数据收集:收集各州的人口数据,包括人口数量、种族、年龄等信息。
2.确定众议院席位总数:根据美国宪法规定,众议院共有435个席位。
3.计算各州的人口比例:将各州的人口数量除以全国总人口,得到各州的人口比例。
4.分配众议院席位:首先给每个州分配一个初始名额;根据各州的人口比例,将众议院席位分配给各州。通常采用的方法是“比例分配法”或“优先分配法”。比例分配法是将众议院席位按照各州的人口比例进行分配,而优先分配法是在比例分配的基础上,对人口较少的州给予一定的额外席位。
5.调整席位分配:由于众议院席位总数是固定的,可能会出现一些州的席位分配不合理的情况。此时,需要进行调整,以确保席位分配的公平性和合理性。
6.划分选区:各州根据分配到的众议院席位数量,划分选区。选区的划分需要遵循一定的原则,如选区的人口数量要大致相等、选区的边界要连续等。
7.选举议员:在划分好的选区内,进行议员选举。选民投票选举代表该选区的议员。
应用场景
- 议会议席分配:如美国国会众议院的议席分配。
- 政治选举:在一些政治选举中,用于确定选区的划分和代表名额的分配。
- 资源分配:可用于其他类似资源分配的问题,如资金、物资等的分配。
- 决策制定:为涉及公平分配的决策提供一种科学的方法和依据。
- 公共政策:在制定公共政策时,考虑人口因素和公平性。
- 地区划分:例如学区划分、选区划分等。
- 组织架构设计:确定不同部门或团队的资源分配和权力分配。
- 国际组织:在一些国际组织中,用于成员国的代表权分配。
算法复杂度
时间复杂度 O(n²)
空间复杂度 O(n)
代码
这里举一个例子,三个群体(人数分别为100, 200, 300),对10个席位进行分配.
若是直接按比例计算1:2:3,那么算出来的席位就不是整数,直接四舍五入就会出现多一个还是少一个的问题.一起看看
def huntington_hill_allocation(num_seats, populations):
"""
根据亨廷顿山算法分配席位。
该算法用于在给定总数的席位中,根据各群体的人口数量进行席位分配。
它旨在提供一个相对公平的分配方法,避免小群体被过度代表或大群体被低估。
参数:
- num_seats: int, 总席位数,需要分配的席位数量。
- populations: List[Tuple[int, int]], 一个列表,其中每个元组包含两个整数,
分别代表群体的人口数量和已经分配的席位数量。
返回:
- List[int], 一个列表,表示每个群体最终分配到的席位数量。
"""
# 计算每个群体的quotient,即人口数量除以(1+已分配席位数)。
# 这是亨廷顿山算法的关键计算步骤,用于确定席位分配的优先级。
quotients = [(i, pop / (1 + seats)) for i, (pop, seats) in enumerate(populations)]
print(quotients)
# 根据quotient值对群体进行降序排序,以便优先分配席位给quotient值最高的群体。
quotients.sort(key=lambda x: x[1], reverse=True)
# 初始化每个群体的席位分配为0,准备进行分配。
seats_allocated = [0] * len(populations)
# 当还有席位剩余时,循环分配席位。
while num_seats > 0:
# 选择当前quotient最高的群体,为其分配一个席位。
index, _ = quotients[0]
seats_allocated[index] += 1
print(quotients)
# 更新该群体的quotient值,考虑到已经分配的额外席位。
quotients[0] = (index, populations[index][0] / (1 + seats_allocated[index]))
# 重新根据quotient值对群体进行排序,确保下一轮分配仍能优先考虑quotient最高的群体。
quotients.sort(key=lambda x: x[1], reverse=True)
# 减少剩余席位数量,表示已经分配了一个席位。
num_seats -= 1
print(f"第{index + 1}洲分配了一个席位后{seats_allocated},剩余席位数量:{num_seats}")
# 返回最终的席位分配结果。
return seats_allocated
# 示例用法
num_seats = 10
populations = [(100, 0), (200, 0), (300, 0)]
# [1, 3, 6]
# populations = [(100, 1), (200, 3), (300, 6)]
# [2, 4, 4]
# 3 7 10
allocated_seats = huntington_hill_allocation(num_seats, populations)
print("分配的席位:", allocated_seats)
"""
[(2, 300.0), (1, 200.0), (0, 100.0)]
第3洲分配了一个席位后[0, 0, 1],剩余席位数量:9
[(1, 200.0), (2, 150.0), (0, 100.0)]
第2洲分配了一个席位后[0, 1, 1],剩余席位数量:8
[(2, 150.0), (1, 100.0), (0, 100.0)]
第3洲分配了一个席位后[0, 1, 2],剩余席位数量:7
[(2, 100.0), (1, 100.0), (0, 100.0)]
第3洲分配了一个席位后[0, 1, 3],剩余席位数量:6
[(1, 100.0), (0, 100.0), (2, 75.0)]
第2洲分配了一个席位后[0, 2, 3],剩余席位数量:5
[(0, 100.0), (2, 75.0), (1, 66.66666666666667)]
第1洲分配了一个席位后[1, 2, 3],剩余席位数量:4
[(2, 75.0), (1, 66.66666666666667), (0, 50.0)]
第3洲分配了一个席位后[1, 2, 4],剩余席位数量:3
[(1, 66.66666666666667), (2, 60.0), (0, 50.0)]
第2洲分配了一个席位后[1, 3, 4],剩余席位数量:2
[(2, 60.0), (1, 50.0), (0, 50.0)]
第3洲分配了一个席位后[1, 3, 5],剩余席位数量:1
[(2, 50.0), (1, 50.0), (0, 50.0)]
第3洲分配了一个席位后[1, 3, 6],剩余席位数量:0
分配的席位: [1, 3, 6]
"""总结
这种方法的优点在于,它在一定程度上能够更公平地按照人口比例分配众议院议员名额,避免了一些其他方法可能出现的不公平或不合理的情况。然而,需要注意的是,没有一种名额分配方法是完全完美的,各种方法都可能存在一定的局限性和争议。在实际应用中,名额分配问题仍然是一个复杂且具有挑战性的议题,需要综合考虑多方面的因素和不同的观点。类似的算法还有比例法,最大余数法,亚当斯法,韦伯斯特法,等额分配法,杰斐逊法.
如果还有更好的名额分配算法,欢迎在评论中支持,大家互相学习.