Merge Sort概述
分而治之算法
递归地将问题分解为多个子问题,直到它们变得简单易解
将解决方案组合起来,解决原有问题
O(n*log(n))运行时间
基于比较的算法的最佳运行时间
一般原则
·合并排序:
1. 将数组分成两半
2.在每一半上调用合并排序以递归排序
3.将两个已排序的两半合并为一个已排序数组
看一个例子:
2,6,5,1,7,4,3
首先第一步,是将数组分成两半,分到直到分不了了。
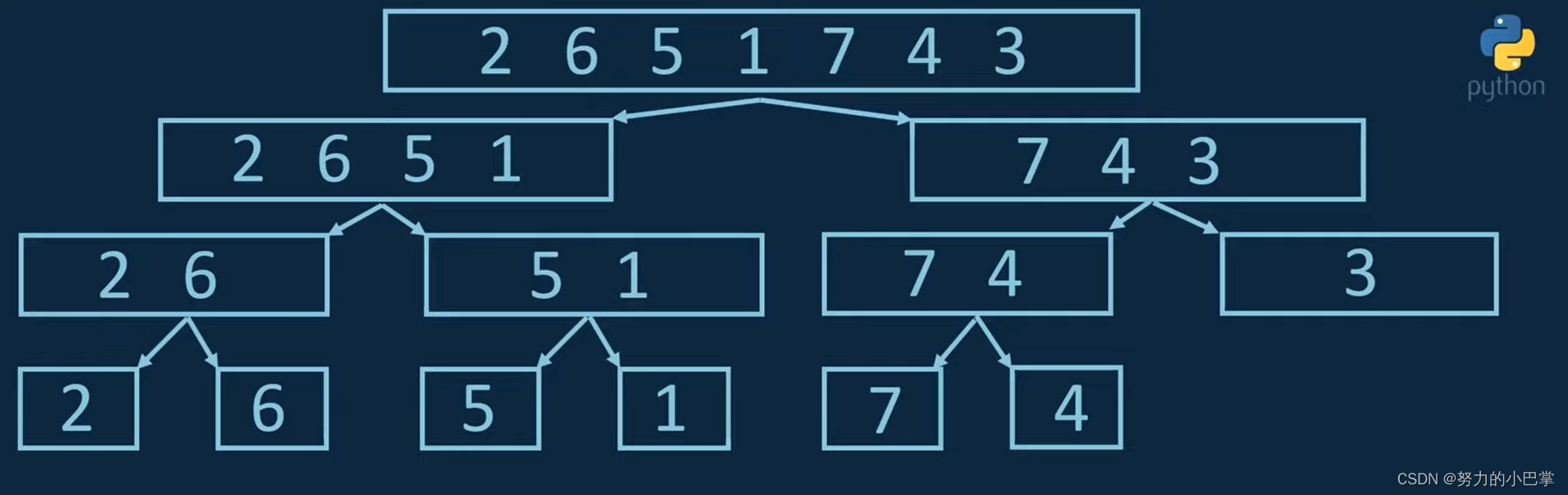
然后现在,对每组数据进行排序。
2,6
1,5
4,7
然后,再一组一组排序:
1,2,5,6
3,4,7
然后最后两组排序
1,2,3,4,5,6,7
注意这里是,1和3比,选1,2和3比,选2,5和3比,选3,4和5比,选4。。。
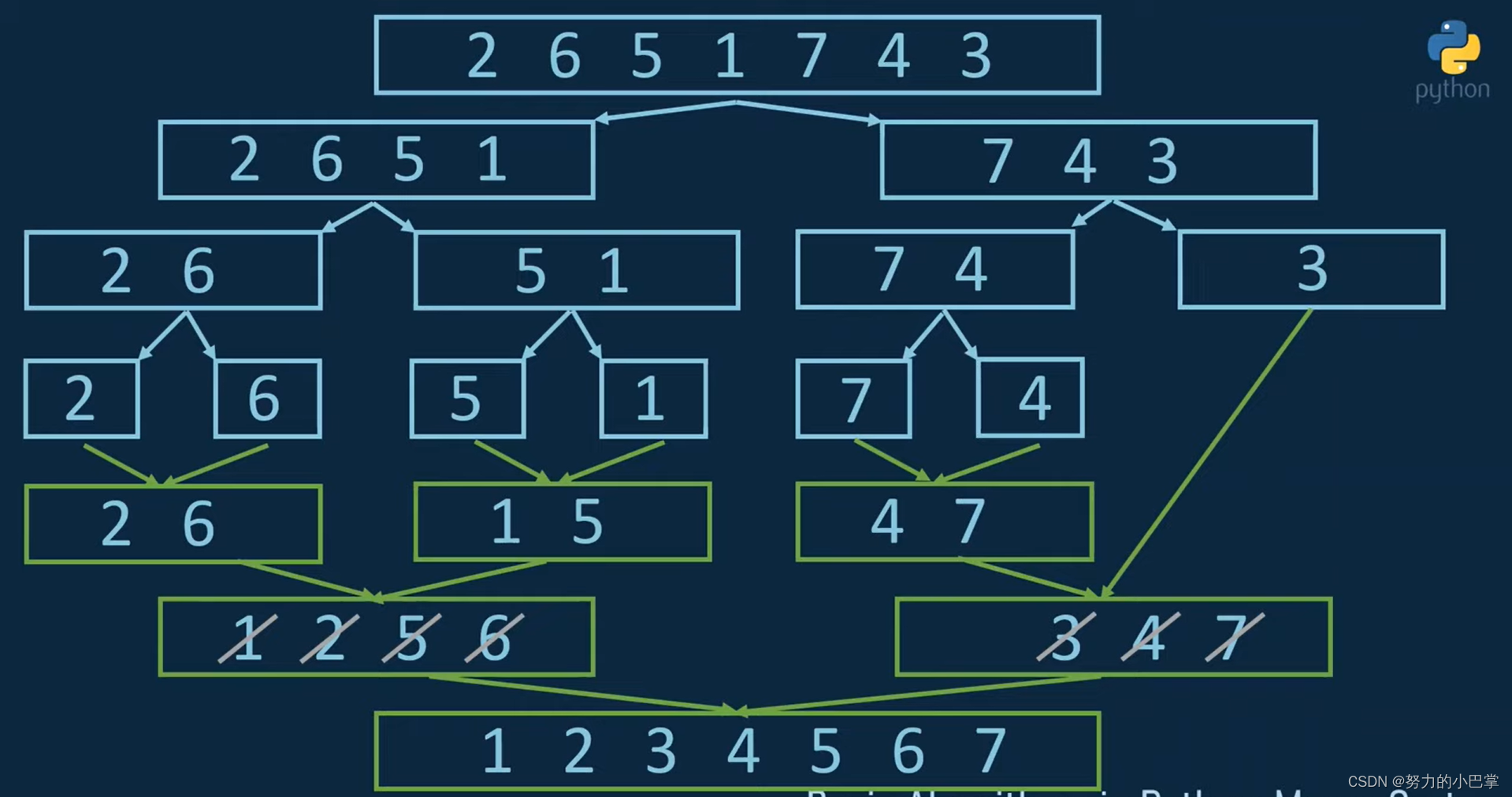
Python实现MergeSort合并排序
def merge_sort(arr):
if len(arr) > 1: #要保证大于1才能排序
left_arr = arr[:len(arr)//2] #定义2个子数组,这个是从索引0到中心点,:左留下空白就是取左边所有
right_arr = arr[len(arr)//2:] #这个是从中心点到右边
# 递归
merge_sort(left_arr)
merge_sort(right_arr) #分别再左右两个数组进行递归
# 执行以上两行以后,左右两个数组都按照顺序排列了
# 合并
# 现在两个数组已经拍好顺序,我们想让两个数组,第一个数组的最左边和第二个数组最左边进行比较
# 所以,创建索引进行追踪
i = 0 #追踪第一个左边数组
j = 0 #追踪右边
k = 0 #追踪合并数组中的索引
while i < len(left_arr) and j < len(right_arr):
if left_arr[i] < right_arr[j]:#如果左边的数组值小
arr[k] = left_arr[i] # 保存索引对应的值
i += 1
#k += 1
#因为我们取得是i的值,所以,必须i+1进入下一个索引,而且,k是合并后的数组,也要进入下一个
else:
arr[k] = right_arr[j]
j += 1
#k += 1
k += 1 #简略后,放这里
# 现在只考虑转移左边的数组,不考虑右边的数组;
# 这是假设,右边都排好了,但是左边没排完
while i < len(left_arr):
arr[k] = left_arr[i]
i += 1
k += 1
# 假设左边都排好了,但是右边还要排
while j < len(right_arr):
arr[k] = right_arr[j]
j += 1
k += 1
arr_test = [2,3,5,1,7,4,4,4,2,6,0]
merge_sort(arr_test)
print(arr_test)问题:
merge_sort(left_arr)
2 merge_sort(right_arr) #分别再左右两个数组进行递归
3 # 执行以上两行以后,左右两个数组都按照顺序排列了 这里是什么意思?是直接调用我定义的函数吗?函数不是没写完吗?这里正是体现了递归函数的工作原理。当你在代码中调用 merge_sort(left_arr) 和 merge_sort(right_arr) 时,你实际上是在调用当前函数自身,但是传入了不同的参数——即左侧子数组和右侧子数组。
虽然从直观上看,函数“还没有写完”,但实际上,每次调用 merge_sort 函数时,它都在执行完整的逻辑流程:
- 检查当前数组的长度是否大于1,如果是,则继续执行。
- 将当前数组分割成两个子数组(左侧和右侧)。
- 对这两个子数组分别递归调用
merge_sort函数。这里就是递归发生的地方,每一次这样的调用都会重复整个过程,直到数组被拆分到不能再拆分(即长度为1或0,视为已排序)。 - 最后,通过合并这些小数组来完成排序。
因此,即便在某次调用中函数尚未执行到合并步骤,之前的调用(处理更小规模数组的那些调用)已经在逐步完成它们的任务。当这些更深层次的递归调用返回时,它们会逐级返回到上一层,最终回到最初的函数调用,这时所有子数组都已经排序完毕,可以进行最终的合并,完成整个数组的排序。