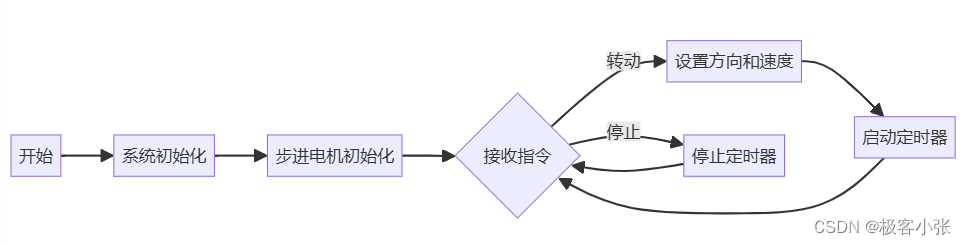
四元数（Quaternion）是一种数学工具，广泛用于计算机图形学、机器人学和物理模拟中，特别适合处理三维旋转。Eigen库是一个高性能的C++数学库，提供了丰富的线性代数功能，其中就包括对四元数的支持。

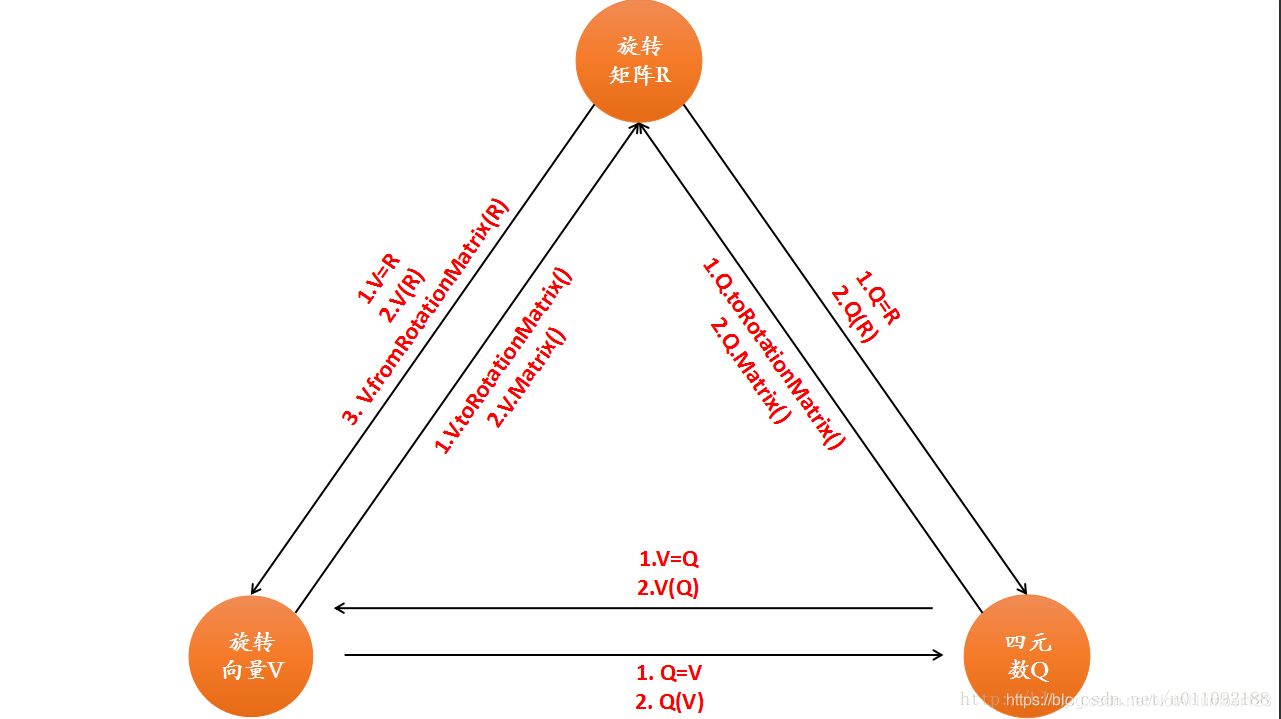
1. 为什么选择四元数？

在计算机图形学和物理学中，四元数被广泛用来表示和计算三维旋转。相比于欧拉角和旋转矩阵，四元数具有以下优点：

• 避免万向锁（Gimbal Lock）：欧拉角在某些情况下会失去一个自由度，而四元数没有这个问题。
• 高效的插值：四元数在进行插值操作时非常方便和高效，这对于动画和平滑运动至关重要。
• 节省空间：四元数只需要4个数来表示一个旋转，而旋转矩阵需要9个数。

2. Eigen库中的四元数类

Eigen库提供了Eigen::Quaternion类和相关的操作来处理四元数。Eigen::Quaternion类定义如下：

template<typename Scalar>
class Quaternion

其中 Scalar 通常为 float 或 double 类型。

3. 四元数的基本操作

创建与初始化

Eigen中可以通过不同的方式创建四元数：

• 默认构造：创建一个未初始化的四元数。
• 直接赋值：通过四个分量（w, x, y, z）来初始化。
• 从旋转矩阵初始化：将旋转矩阵转换为四元数。

示例代码如下：

#include <Eigen/Geometry>
#include <iostream>

int main() {
    // 通过直接赋值初始化
    Eigen::Quaternionf q1(1.0, 0.0, 0.0, 0.0);
    std::cout << "q1: " << q1.coeffs().transpose() << std::endl;

    // 从旋转矩阵初始化
    Eigen::Matrix3f rot;
    rot = Eigen::AngleAxisf(M_PI / 4, Eigen::Vector3f::UnitZ());
    Eigen::Quaternionf q2(rot);
    std::cout << "q2: " << q2.coeffs().transpose() << std::endl;

    return 0;
}

四元数和旋转矩阵的转换

四元数可以轻松转换为旋转矩阵，反之亦然：

// 四元数转旋转矩阵
Eigen::Matrix3f rotationMatrix = q2.toRotationMatrix();

// 旋转矩阵转四元数
Eigen::Quaternionf q3(rotationMatrix);

 四元数乘法

四元数乘法用于组合旋转：

Eigen::Quaternionf q4 = q1 * q2;
std::cout << "q4: " << q4.coeffs().transpose() << std::endl;

四元数的共轭与逆

四元数的共轭与逆可以方便地计算：

Eigen::Quaternionf q_conjugate = q1.conjugate();
Eigen::Quaternionf q_inverse = q1.inverse();
std::cout << "Conjugate: " << q_conjugate.coeffs().transpose() << std::endl;
std::cout << "Inverse: " << q_inverse.coeffs().transpose() << std::endl;

4. 四元数插值

四元数插值（Spherical Linear Interpolation, Slerp）在动画和旋转平滑中非常有用。Eigen提供了Eigen::Quaternion类的slerp函数来实现四元数的插值：

Eigen::Quaternionf q5 = q1.slerp(0.5, q2);
std::cout << "Slerped Quaternion: " << q5.coeffs().transpose() << std::endl;

5. 结语

Eigen库中的四元数类提供了强大的工具来处理三维旋转和插值。通过Eigen库，我们可以轻松实现四元数的创建、操作和插值，从而简化复杂的三维旋转问题。