学习视频:第3章-二分类线性判别分析_哔哩哔哩_bilibili
西瓜书对应章节: 3.4
文章目录
- - 算法原理
- - 损失函数推导
- -- 异类样本中心尽可能远
- -- 同类样本方差尽可能小
- -- 综合
- 知识点补充 - 二范数
- 二范数(2-norm)详解
- 定义
- 几何意义
- 性质
- 应用
- 示例
- 求解 w
- 知识点补充 - 广义瑞利商
- 定义
- 解释
- 应用
- 优化广义瑞利商
- 算法原理

- 损失函数推导
--------------------------------------- 投影后 ----------------------------------------------
– 异类样本中心尽可能远
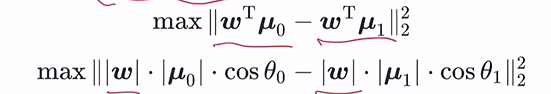
– 同类样本方差尽可能小
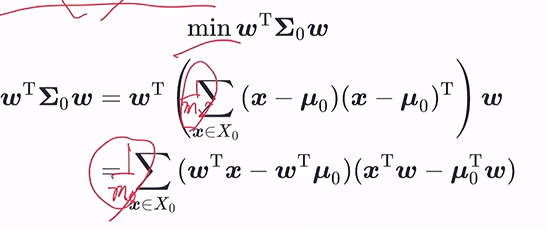
– 综合
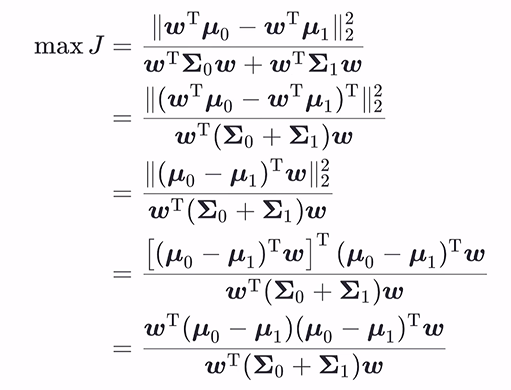
分母为 同类样本之间的关系,分子为异类样本之间的关系,使分子尽量小(同类样本方差尽可能小),分母尽量大(异类样本中心尽量远),则有 M a x Max Max J J J
知识点补充 - 二范数
二范数(2-norm)详解
定义
对于一个n维欧几里得空间中的向量 x = [ x 1 , x 2 , … , x n ] T \mathbf{x} = [x_1, x_2, \ldots, x_n]^\text{T} x=[x1,x2,…,xn]T,其二范数定义为: ∥ x ∥ 2 = x 1 2 + x 2 2 + ⋯ + x n 2 = x T x \|\mathbf{x}\|_2 = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2} = \sqrt{\mathbf{x}^\text{T} \mathbf{x}} ∥x∥2=x12+x22+⋯+xn2=xTx
几何意义
在二维或三维空间中,二范数表示向量末端到原点的欧几里得距离。例如,在二维空间中,向量
x
=
[
x
1
,
x
2
]
T
\mathbf{x} = [x_1, x_2]^\text{T}
x=[x1,x2]T 的二范数表示为:
∥
x
∥
2
=
x
1
2
+
x
2
2
\|\mathbf{x}\|_2 = \sqrt{x_1^2 + x_2^2}
∥x∥2=x12+x22
这正是勾股定理的直接应用,表示向量
x
\mathbf{x}
x 在平面上的长度。
性质
非负性:对于所有向量 x , ∥ x ∥ 2 ≥ 0 ,且 ∥ x ∥ 2 = 0 当且仅当 x = 0 \mathbf{x},\|\mathbf{x}\|_2 \geq 0,且 \|\mathbf{x}\|_2 = 0 当且仅当 \mathbf{x} = \mathbf{0} x,∥x∥2≥0,且∥x∥2=0当且仅当x=0。齐次性:对于所有向量 x \mathbf{x} x 和所有标量 c c c, ∥ c x ∥ 2 = ∣ c ∣ ∥ x ∥ 2 \|c\mathbf{x}\|_2 = |c|\|\mathbf{x}\|_2 ∥cx∥2=∣c∣∥x∥2。三角不等式:对于所有向量 x \mathbf{x} x 和 y \mathbf{y} y, ∥ x + y ∥ 2 ≤ ∥ x ∥ 2 + ∥ y ∥ 2 \|\mathbf{x} + \mathbf{y}\|_2 \leq \|\mathbf{x}\|_2 + \|\mathbf{y}\|_2 ∥x+y∥2≤∥x∥2+∥y∥2。
应用
二范数在数值分析、机器学习、信号处理等领域有广泛应用。例如,在机器学习中,二范数常用于正则化项,以防止模型过拟合;在信号处理中,二范数用于衡量信号的能量。
示例
考虑向量 x = [ 3 , 4 ] T \mathbf{x} = [3, 4]^\text{T} x=[3,4]T,其二范数为: ∥ x ∥ 2 = 3 2 + 4 2 = 9 + 16 = 25 = 5 \|\mathbf{x}\|_2 = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 ∥x∥2=32+42=9+16=25=5。
这表示向量 (\mathbf{x}) 在二维空间中的长度为5。
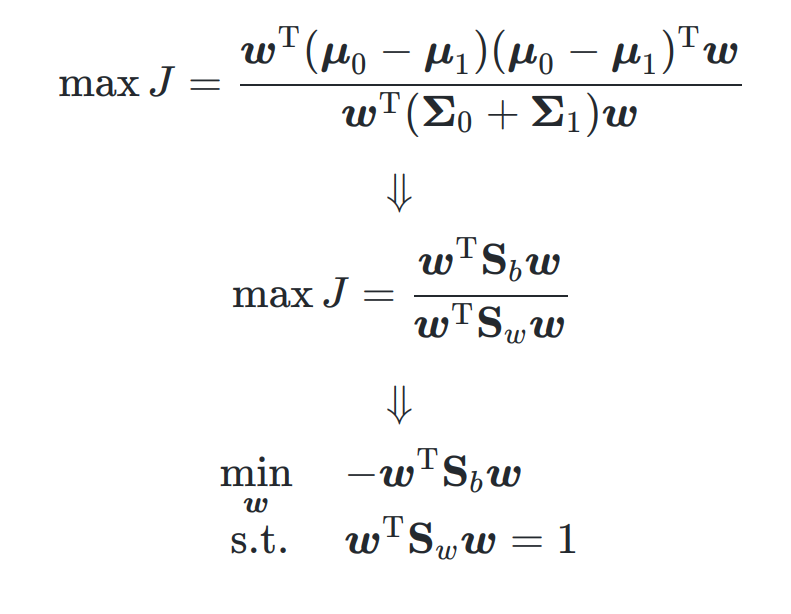
求解 w
- 利用 拉格朗日乘子法 对该式子进行转化


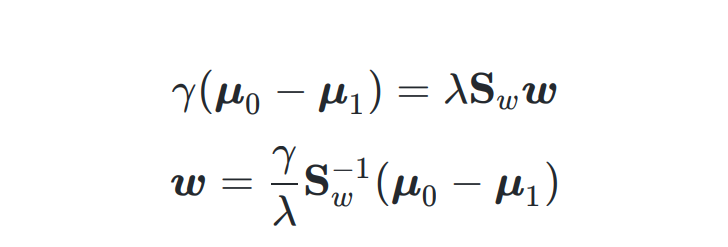
知识点补充 - 广义瑞利商
广义瑞利商(Generalized Rayleigh Quotient)是一种在数学和工程中广泛使用的概念,特别是在信号处理、模式识别和最优化问题中。它是经典瑞利商的推广,用于衡量向量在不同矩阵(通常是对称正定矩阵)下的分布情况。
定义
广义瑞利商的形式如下:
R ( w ) = w ⊤ A w w ⊤ B w R(\mathbf{w}) = \frac{\mathbf{w}^\top \mathbf{A} \mathbf{w}}{\mathbf{w}^\top \mathbf{B} \mathbf{w}} R(w)=w⊤Bww⊤Aw
其中, A \mathbf{A} A 和 B \mathbf{B} B 是对称矩阵, B \mathbf{B} B 通常是正定的, w \mathbf{w} w 是一个非零向量。
解释
- A \mathbf{A} A 通常表示待优化的问题中涉及的矩阵,例如散布矩阵或相关矩阵。
- B \mathbf{B} B 通常表示一个约束矩阵,比如在模式识别中的类内散布矩阵或协方差矩阵。
- w \mathbf{w} w 是我们要寻找的向量,使得广义瑞利商 R ( w ) R(\mathbf{w}) R(w) 达到最大或最小。
应用
-
线性判别分析 (LDA):
在模式识别中,LDA 通过最大化类间散布矩阵 S \mathbf{S} S与类内散布矩阵 S w \mathbf{S}_w Sw的广义瑞利商来找到最优的投影方向:
R ( w ) = w ⊤ S b w w ⊤ S w w R(\mathbf{w}) = \frac{\mathbf{w}^\top \mathbf{S}_b \mathbf{w}}{\mathbf{w}^\top \mathbf{S}_w \mathbf{w}} R(w)=w⊤Swww⊤Sbw -
特征值问题:
广义瑞利商的极值问题可以转化为广义特征值问题,解决矩阵 A w = λ B w \mathbf{A}\mathbf{w} = \lambda \mathbf{B}\mathbf{w} Aw=λBw 中的特征值 λ \lambda λ 和特征向量 w \mathbf{w} w。 -
振动分析:
在结构工程和机械工程中,用于分析系统在不同状态下的振动模式。
优化广义瑞利商
求解广义瑞利商最大化或最小化的问题通常涉及求解广义特征值问题:
A
w
=
λ
B
w
\mathbf{A} \mathbf{w} = \lambda \mathbf{B} \mathbf{w}
Aw=λBw
其中,
λ
\lambda
λ 是广义瑞利商的极值。
通过解这个特征值问题,可以得到使广义瑞利商达到极值的 w \mathbf{w} w 和对应的特征值 λ \lambda λ。