记忆化搜索
- 1.记忆化搜索
- 2.不同路径
- 3.最长递增子序列
- 4. 猜数字大小 II
- 5.矩阵中的最长递增路径

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
1.记忆化搜索
什么是记忆化搜索,下面我们以一道比较常见的509. 斐波那契数来演示一下什么是记忆化搜索。
关于这个斐波那契数,我们很早之前就碰到过如循环、递推、递归,不过它 还可以用动态规划,记忆化搜索来解决。矩阵快速幂也可以解决。
循环、递推、递归,时间复杂度O(N^2)
动态规划、记忆化搜索,时间复杂度O(N)
矩阵快速幂,时间复杂度O(logN)
因为记忆化搜索是基于递归代码来实现的,所以我们先用递归写这道题。
解法一:递归

dfs要干的事情就是给我一个数我把它第n个斐波那契数返回来。关于函数体怎么写,很简单求。F(0) = 0,F(1) = 1,F(n) = F(n - 1) + F(n - 2),其中 n > 1。求第n个斐波那契数先把n-1和n-2斐波那契数求出来。递归出口 n<=1 返回n就可以了。
int fib(int n)
{
return dfs(n);
}
int dfs(int n)
{
if(n <= 1) return n;
return dfs(n-1)+dfs(n-2);
}
我们先分析一下这个递归过程。当n=5的时候,我们看一下这个递归展开过程。就像一颗二叉树。有多少节点就要递归多少次。时间复杂度O(2^N)
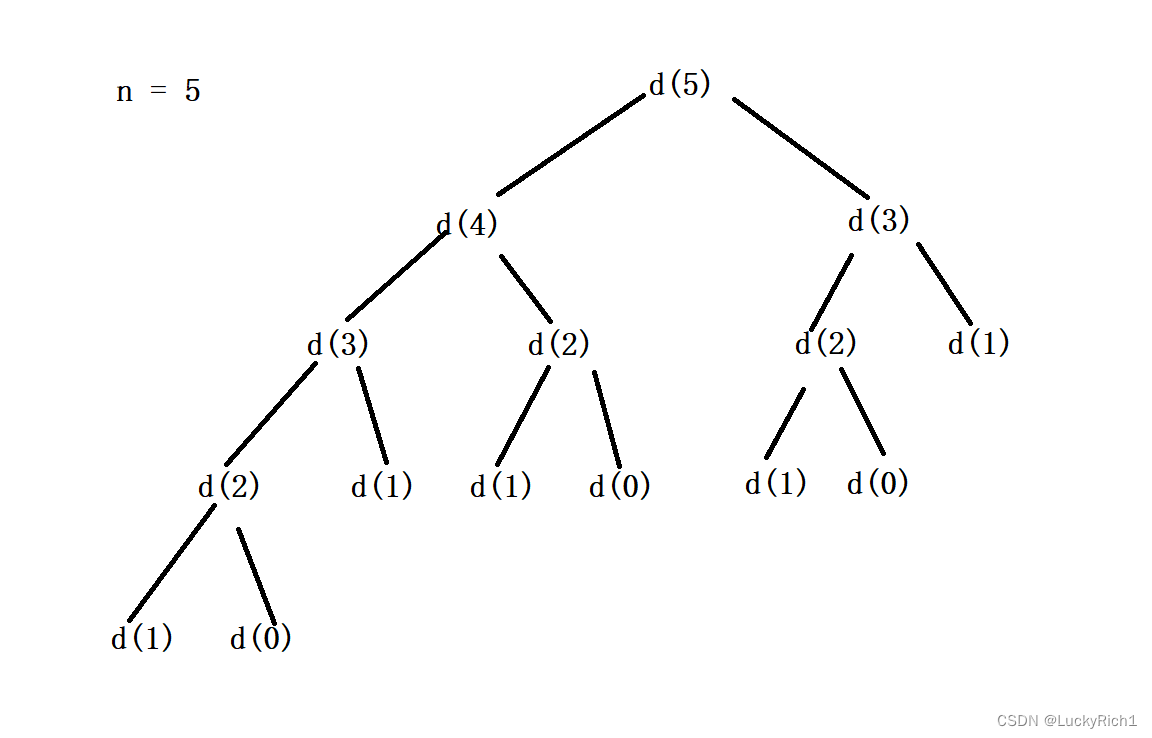
我们先分析一下为什么这个递归它会这么慢。慢其实就慢在我们会重复计算一些问题,如d(3)我们会重复进入两次,但是这两个d(3)的递归展开树是完全一样的!这两个d(3)向上返回的值是完全一样的!
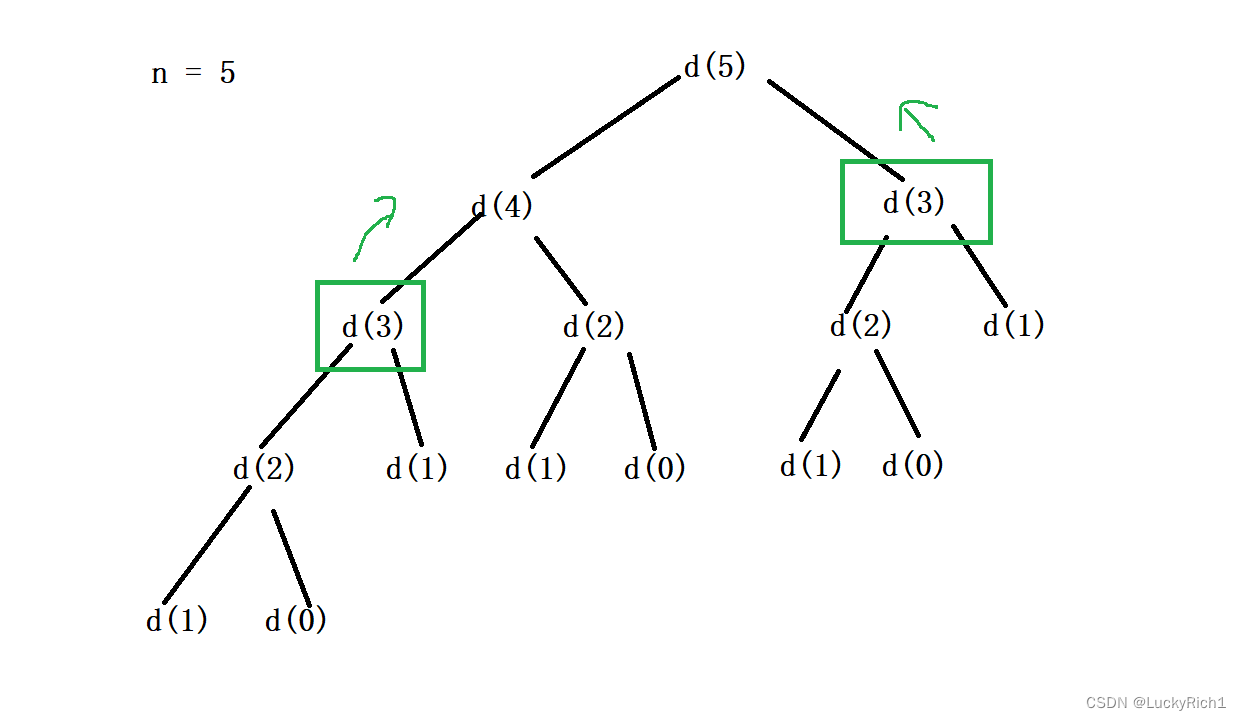
那我们想一下能不能这样优化一下,来一个备忘录,就是当我从d(5)来深度优先遍历的时候,先去左边,然后当我从d(3)这颗递归树返回时是一个返回值,(x为返回值)此时把这个d(3)=x这个f信息丢到备忘录里。(备忘录可能是一个数组、哈希表)。
然后当从左边回来然后去右边的时候,当我们又一次进入d(3)的时候,此时我就不把d(3)展开了。因为此时我去备忘录里找找我发现d(3)=x这个消息在左边就已经计算过了。所以在这里不展开了直接在备忘录里把x给拿出来,然后返回就可以了。
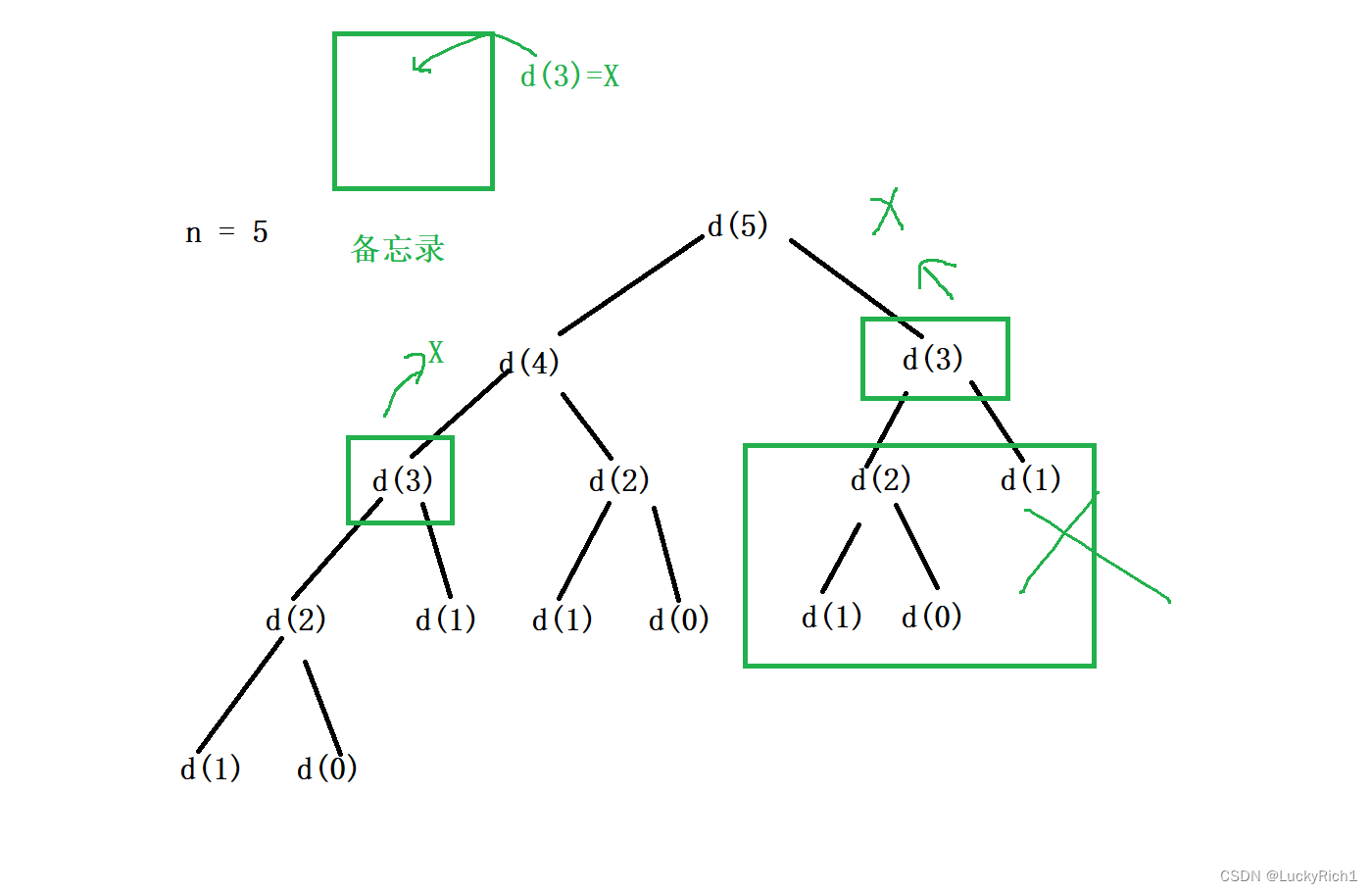
当有一个备忘录的时候,相同子树不在展开的时候,是不是就对递归做优化了。像这样一种方式就叫做记忆化搜索!
解法二:记忆化搜索
在递归过程中,发现有一些完全相同的问题时,我们就可以把完全相同问题的结果放到备忘录里,然后递归进入相同问题的时候直接往备忘录里拿结果就可以了。这就是记忆化搜索,因此又称作带备忘录的递归。
此时你会发现其实并不止d(3)会被做优化其实就是剪枝,d(2)也会被优化。这么多分支都不用进去。时间复杂度直接从O(2^N)变成O(N)。所以添加一个备忘录可以极大优化我们的搜索过程。这也是记忆化搜索名字的由来,带着记忆去做dfs,这些重复的地方就不要重复进去了就实现了大量的剪枝,时间复杂度从指数级别降到线性级别!
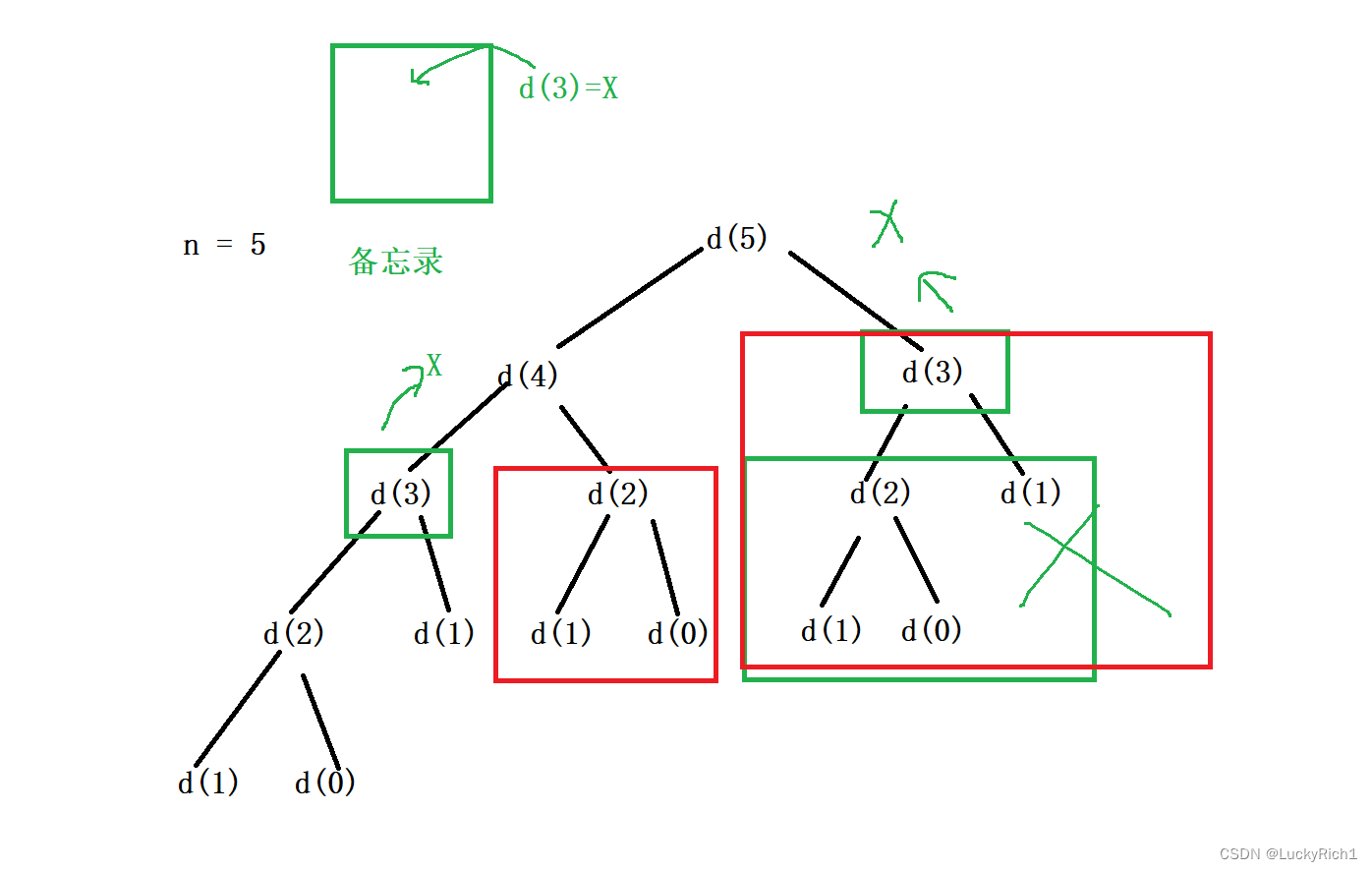
如何实现记忆化搜索呢?
- 添加一个备忘录
- 递归每次返回的时候,将结果放到备忘录里面
- 在每次进入递归的时候,往备忘录里面瞅一瞅
那添加一个什么样的备忘录呢?
紧盯这样一个原则,先找可变参数,然后将<可变参数,返回值>的映射关系存起来。
在这个dfs递归函数里。可变参数就是n,返回值就是第几个斐波那契数。所以在这里仅需<int,int> 前面是第几个斐波那契数的第几,后面是存的是具体的斐波那契数。
这个备忘录搞什么数据结构呢?
可以搞一个哈希表,这里我们可以来一个数组就行。这个数组可以搞成全局的,也可以当成dfs参数。
有时候备忘录可能需要初始化一下。搞成全局的备忘录里都是0,但是我们备忘录里有一个规则,备忘录里面初始存的值不能跟最终结果的值是一样的。 也就是说要去备忘录找这个值的时候,我得先判断一下你这个值是不是已经被计算过了,如果这个备忘录里面d(3)本来就存在X值,但是我还没有进入过d(3)里呢,就可能会导致误差。所有要把备忘录初始化为这个dfs里永远都不会出现得返回值!

int memo[31];
int fib(int n)
{
// 2.记忆化搜索
//初始化
memset(memo, -1 ,sizeof memo);
// 1. 递归
//return dfs(n);
}
int dfs(int n)
{
//往备忘录查找一下
if(memo[n] != -1) return memo[n]; //剪枝
if(n <= 1)
{
memo[n]=n;// 返回之前放进备忘录里面
return n;
}
memo[n]=dfs(n-1)+dfs(n-2);// 返回之前放进备忘录里面
return memo[n];
}
解法三:动态规划
动态规划我们一般思路是盯着5个方向。
- 确定状态表示
- 推导状态转移方程
- 初始化
- 确定填表顺序
- 确定返回值
解决动态规划问题现创建一个表格。可能是一维的也可能是二维的。我称为dp表。我们会赋予现赋予dp表一个含义。如果有一个i下标,我们会赋予dp[i] 一个含义。其中这个dp[i]的含义就是状态表示。推导这个状态转移方程就我想求这个dp[i]的值的时候,我们会从前面填的表格的值来推导dp[i]是多少。具体推导处理的公式就是状态转移方程。初始化就是我们填dp[i]是依赖之前填的表格,但是0这个位置状态没有办法搞。因此必须先把0这个位置的值先初始化放后序填表。确定填表顺序 如果填dp[i]状态依赖于之前的状态,就必须是从左到右。确定返回值 根据题目要求确定最后返回的是这个表中那一个数。
其实我们可以从之前的递归和记忆化搜索直接推出这5步,因为它们是一一对应的关系。
dfs函数头就是给我一个数n我返回数n的斐波那契数。
填写备忘录的顺序,我们是做了深度优先遍历因此会一直递归下去,所以先会把d(1),dp(0)先放到备忘录里然后在往上返回一依次放。对应dp表就是从左到右。
主函数是dfs(n)调用的,对应dp表返回的就是dp[n]的值。
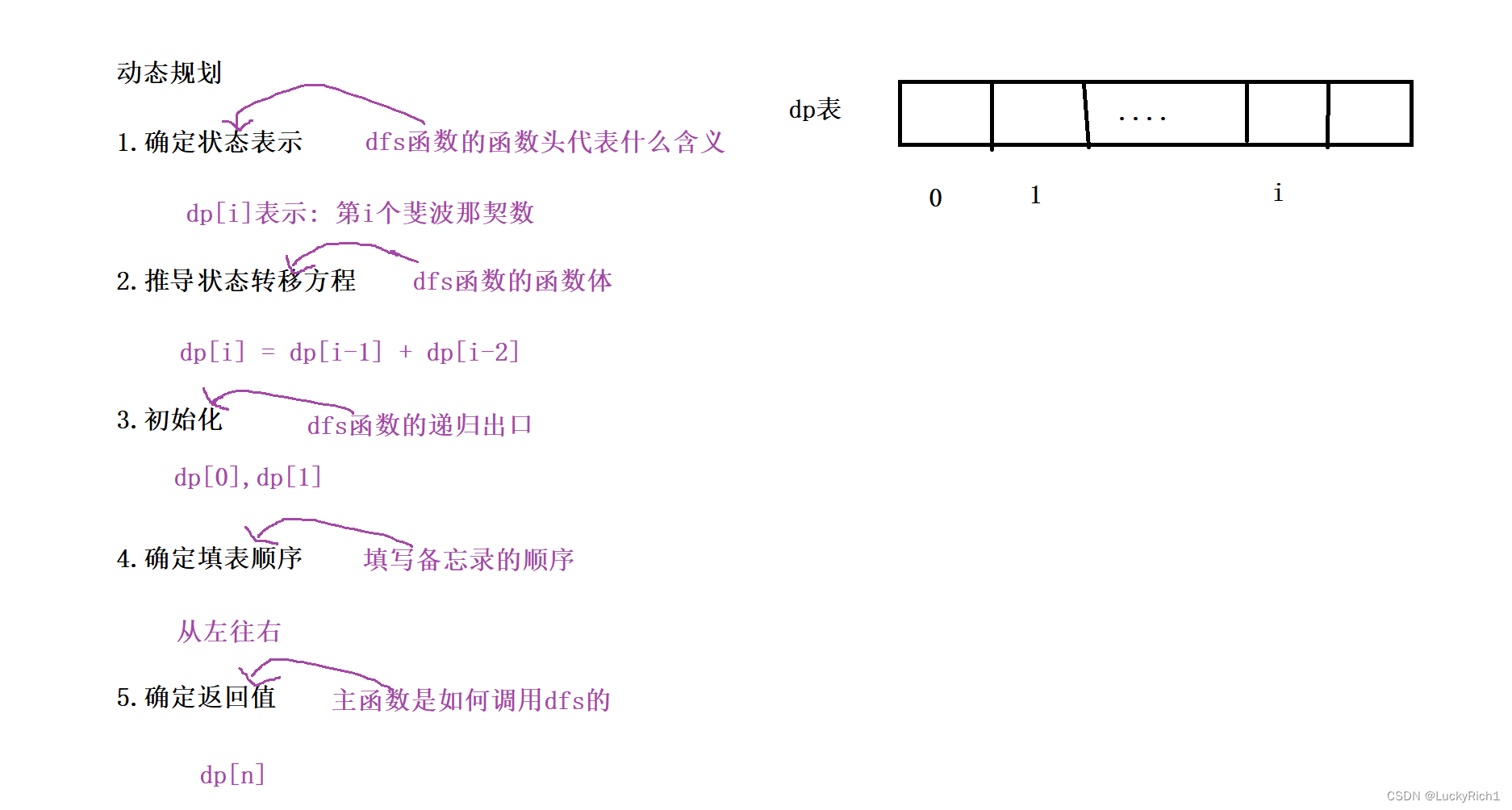
为什么动态规划和记忆化搜索这些都是一一对应的?因为动态规划和记忆化搜索本质都是一样的:
- 暴力求解(暴搜),动态规划要求dp[i]也要把前面都算出来,也是暴搜。无非就是动态规划和记忆化搜索是对暴搜的优化。
- 对暴力解法的优化是一样的:把已经计算过的值,存起来。 记忆化搜索算d(5),因为d(4)和d(3)已经放进备忘录里面了。直接去备忘录里找拿d(4)和d(3)就看可以。动态规划求dp[i]的时候是已经把前面dp[i-1]和dp[i-2]的值已经放到这个表里面了,然后求dp[i]的时候,直接去表里拿就就可以了。
《算法导论》这本书就是把记忆化搜索和常规的动态规划 归为 动态规划。无法就是记忆化搜索是递归形式的动态规划,而常规的动态规划是一个递推(循环)动态规划。
int dp[31];
int fib(int n){
// 3. 动态规划
dp[0]=0,dp[1]=1;
for(int i = 2; i <= n; ++i)
dp[i] = dp[i - 1] + dp[i - 2];
return dp[n];
}
下面我们总结几个问题。
1.所有的递归(暴搜、深搜),都能改成记忆化搜索吗?
不是的,只有在递归过程中,出现大量完全相同的问题时,才能用记忆化搜索的方式优化。
2.带备忘录的递归、带备忘录的动态规划、记忆化搜索 都是一回事。
3.自顶向下 vs 自底向上 有什么不同。
无法就是解决一个问题时思考方向不同而已。自顶向下就是思考决策树时是按照从上往下的顺序来思考的,我想求d(5),我要先求出d(4)和d(3) 。。。。。自底向上就是从下往上思考,求d(5),我从最底下看,我先求d(0) d(1)推出d(2),然后在求d(3)。。。 而这两种方式就正好对应记忆化搜索和常规动态规划。记忆化搜索是递归加一个备忘录所以记忆化搜索方式就是从上往下。常规动态规划是递推方式,先求dp[0],自下往上对推导dp[n]是多少。
4.我们在解决这个问题的时候发现了一个流程,我可以先写出暴搜,然后改成记忆化搜索,然后把记忆化搜索东西抽象处理就是动态规划。好像发现解决动态规划问题的全新流程,暴搜->记忆化搜索->动态规划。以前是 常规动态规划。
碰到一道动态规划的题先写成暴搜,然后改成记忆化搜索,在抽象成成动态规划。一般这样搞也没错,但是有些题你直接写出暴搜会比你用常规动态规划成本高的多。
暴搜->记忆化搜索->动态规划 和 常规动态规划 都是解决动态规划的方式。
那个更好, 因人而异,因题而异。
在我看来暴搜可以为我们确定状态表示,提供一个方向。 而且记忆化搜索就已经是一个动态规划了,从暴搜改到记忆化搜索时间复杂度已经是线性级别了,没有必要在搞成动态规划了。
2.不同路径
题目链接:62. 不同路径
题目分析:

这个机器人位于左上角位置,每次只能向右和向下移动,问从开始位置到终点一共有多少种不同的路径。
我们下标从1开始计数,这样就少了很多边界情况。
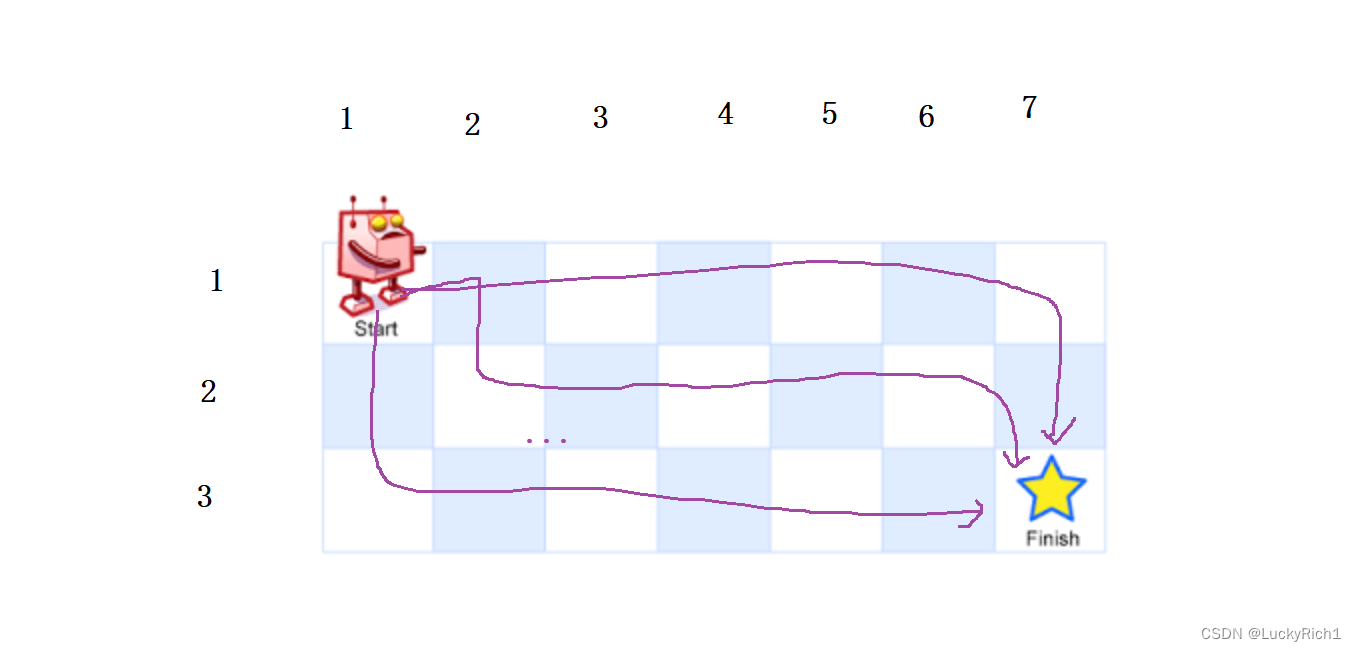
算法原理:
接下来我们用记忆化搜索解决这个问题。如果纯记忆化搜索我们只要两步就可以了。第一步 先想出暴搜(递归)的代码。第二步 暴搜代码改成记忆化搜索,但是前提是能否改!
1.暴搜(递归)
我们最后向求出的m,n位置有多少种不同的走法,那么就这样搞dfs,dfs我给你两个参数,dfs(i,j) 你直接给我返回1,1到达i,j有多少种走法。具体dfs你内部怎么走我不关心,我相信你一定能够完成任务。接下来想想这个函数体 如何设计,我想从1,1到达这个三角的位置一共有多少种方式,其实只用关心两个位置就可以。因为想到达三角的位置,必须要从这两个圆圈到达,要求只能向右走向下走。
如果此时我知道到达圆圈有多少种方式那在多走一步就走到三角了。也就是说到达圆圈有多少种方式,到达这个三角也有多少种方式。因此仅需要达到两个圆圈有多少种方式加起来就是到达三角位置的方式 dfs(i-1,j) + dfs(i,j-1)。
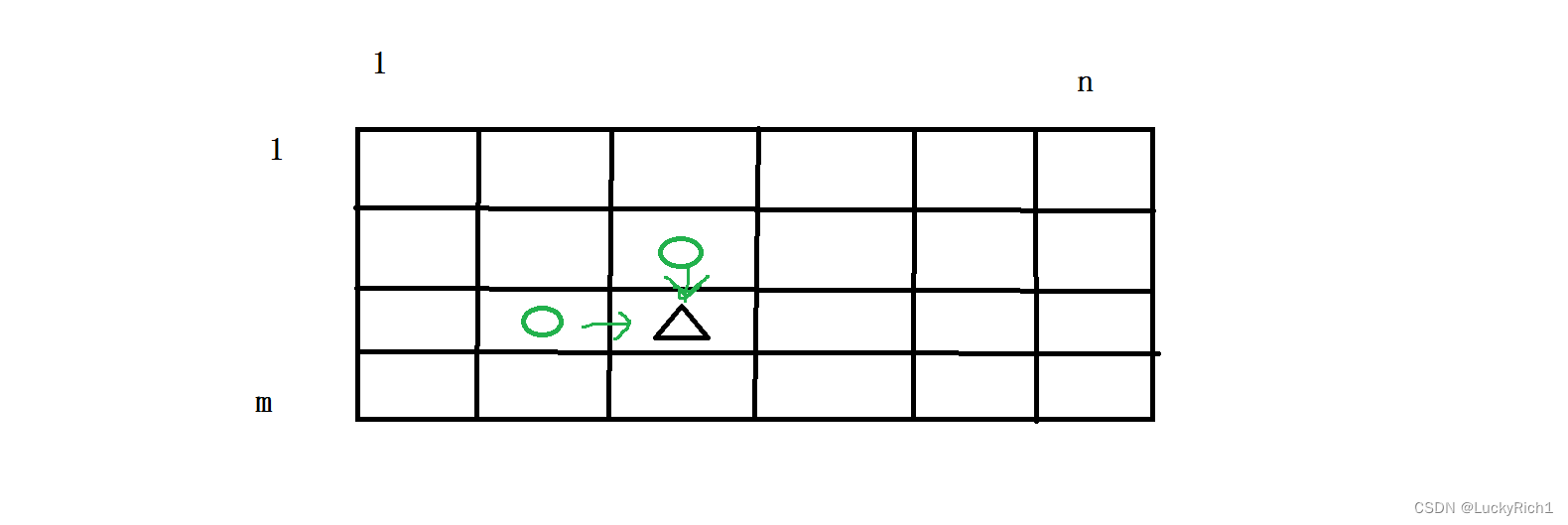
递归出口 我们考虑某个位置的时候,我们仅会考虑它上面的位置以及左边的位置。有可能i=1的时候去考虑i-1不就越界了吗,i=0的时候不能从非法位置达到这里。同理j=0也是一种非法情况,我们既要考虑上边也要考虑左边。因此
i == 0 || j == 0 return 0;
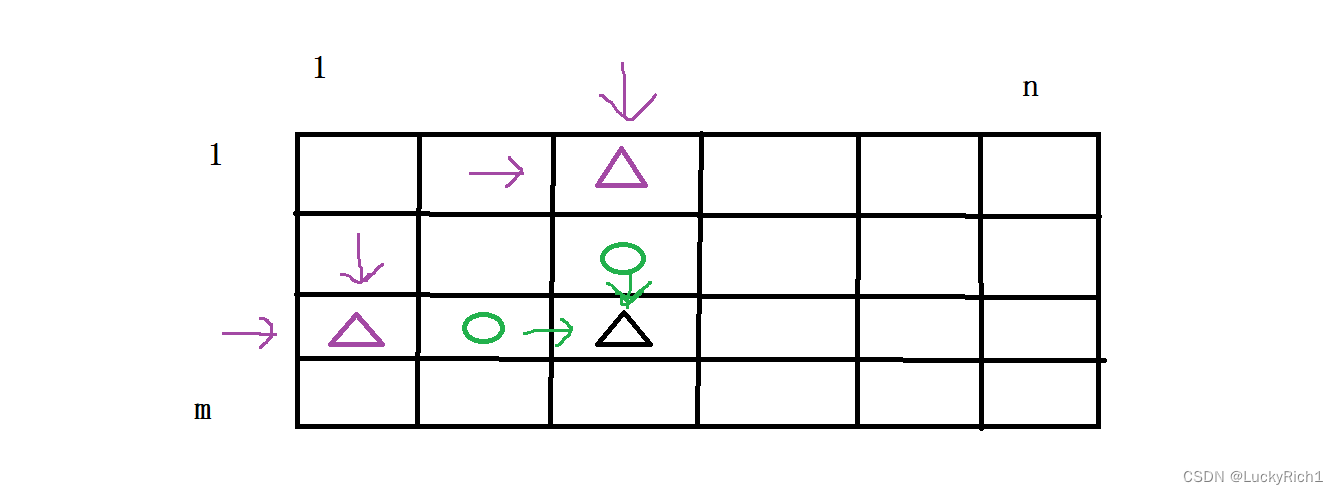
但还有一种隐藏递归出口,当i == 1 && j == 1的时候是位于起点的,上面和左边都没有所以需要特殊处理 i == 1 && j == 1 return 1
class Solution {
public:
int uniquePaths(int m, int n)
{
return dfs(m,n);
}
int dfs(int i,int j)
{
if(i == 0 || j == 0)
return memo[i][j];
if(i == 1 && j == 1)
return 1;
return dfs(i-1,j)+dfs(i,j-1);
}
};
上面会超时,下面看看能否暴搜的代码改成记忆化搜索。在递归过程种发现大量重复的相同问题就可以用记忆化搜索。
记忆化搜索
我们发现在递归过程种发现大量重复的相同问题因此可以用记忆化搜索
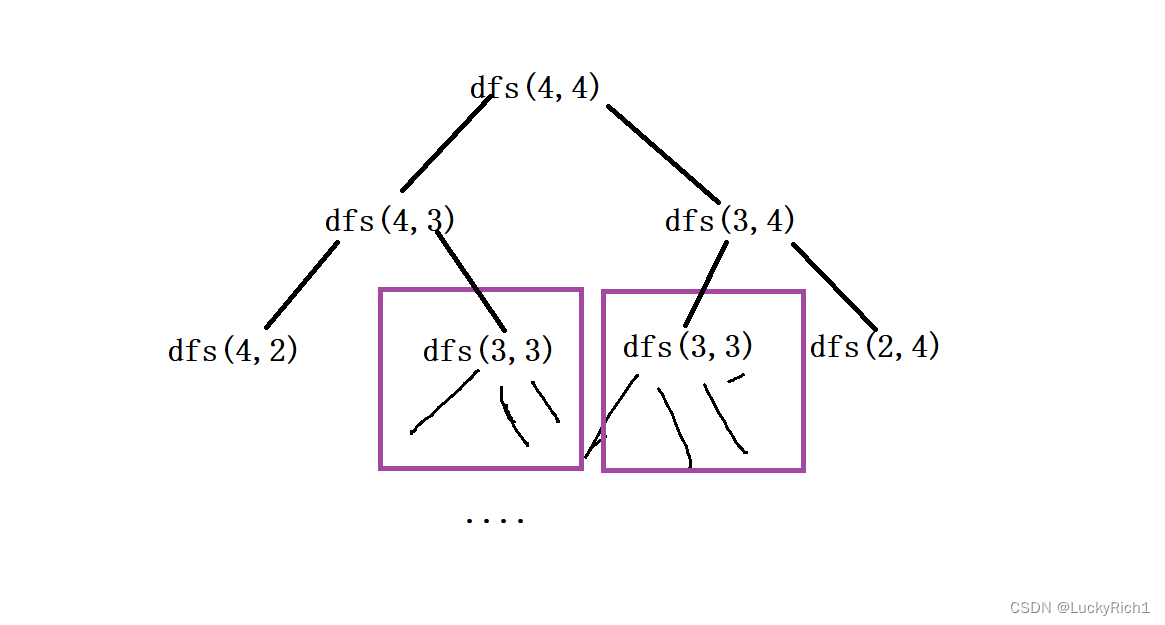
- 搞一个备忘录
- 递归之前,查找一下备忘录
- 返回之前,把结果存在备忘录中
搞一个备忘录 上一道题是搞一个一维数组,但是这道题dfs函数里面是有两个可变参数,i和j一直在变化。里面的值是int,因此我可以搞一个int [m+1][n+1] 二维数组。因为要访问到m,n的位置。
class Solution {
int memo[101][101];
public:
int uniquePaths(int m, int n) {
// 记忆化搜索
return dfs(m,n);
}
int dfs(int i,int j)
{
if(memo[i][j] != 0) return memo[i][j];
if(i == 0 || j == 0)
{
memo[i][j] = 0;
return memo[i][j];
}
//return 0;
if(i == 1 && j == 1)
{
memo[i][j] = 1;
return memo[i][j];
}
memo[i][j]=dfs(i-1,j)+dfs(i,j-1);
return memo[i][j];
}
};
解下来把记忆化搜索改成动态规划。
class Solution {
int dp[101][101]; //先创建一个dp表 dp[i][j]表示到达i,j有多少种方式
public:
int uniquePaths(int m, int n) {
// 动态规划
dp[1][1] = 1; // 初始化
for(int i = 1; i <= m; ++i)
{
for(int j = 1; j <= n; ++j)
{
if(i == 1 && j == 1) continue;
dp[i][j] = dp[i-1][j] + dp [i][j-1];//状态转移方程
}
}
return dp[m][n];
}
};
3.最长递增子序列
题目链接:300. 最长递增子序列
题目分析:
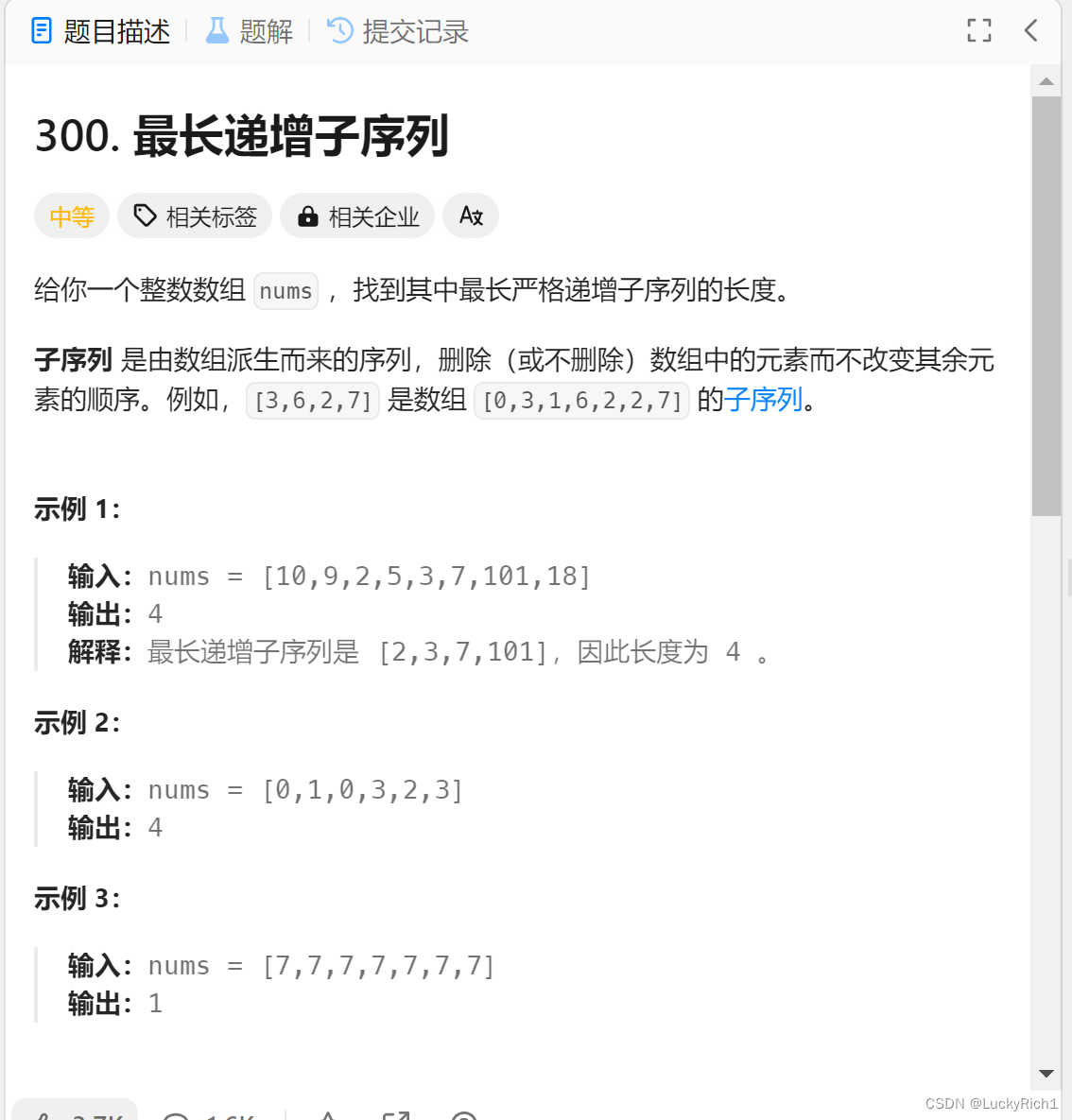
子序列是数组中可以不连续的的序列。让找的是最长的子序列。最长子序列不止一个但是返回的是最长的长度。
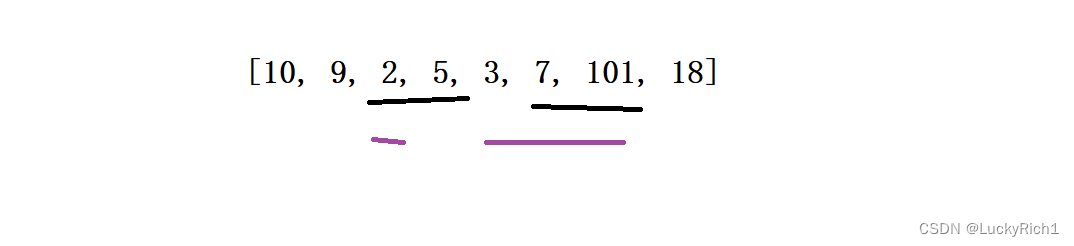
算法原理:
还是用记忆化搜索方式,分两步,第一步 暴搜,第二步 暴搜->记忆化搜索
暴搜
如何暴力的把最长递增子序列长度找出来,其实我们能够暴力的把所有递增子序列找到然后找到其中最长的长度不就可以了。如何暴力,很简单画个决策树,最长子序列可能回一任何一个起点开始,所以刚开始可能以2、5、3、7、101、18所有情况为起点,然后递归下去,如从2递归下去,只能从2后面的元素考虑,注意只能选择比2大的。选择5然后从5递归下去,只能选择比5大的等等。
接下来思考一下这个递归函数如何设计,函数头 我们看我们每次都是干的什么事情,每次我们都以某个位置为起点,找到以这个起点开始的最长递增子序列的长度。int dfs(pos),函数体 来一个for循环,让i从pos+1位置开始循环一直到n,因为考虑以pos位置为起点,接下来考虑的是pos+1位置,然后找到所有情况的最大值,然后在加上一个1就可以了,因为当前位置也要算上!for(int i=pos+1; i<n;++i) max(dfs(i)+1)。递归出口 不需要递归出口,把所有情况走完就返回了。
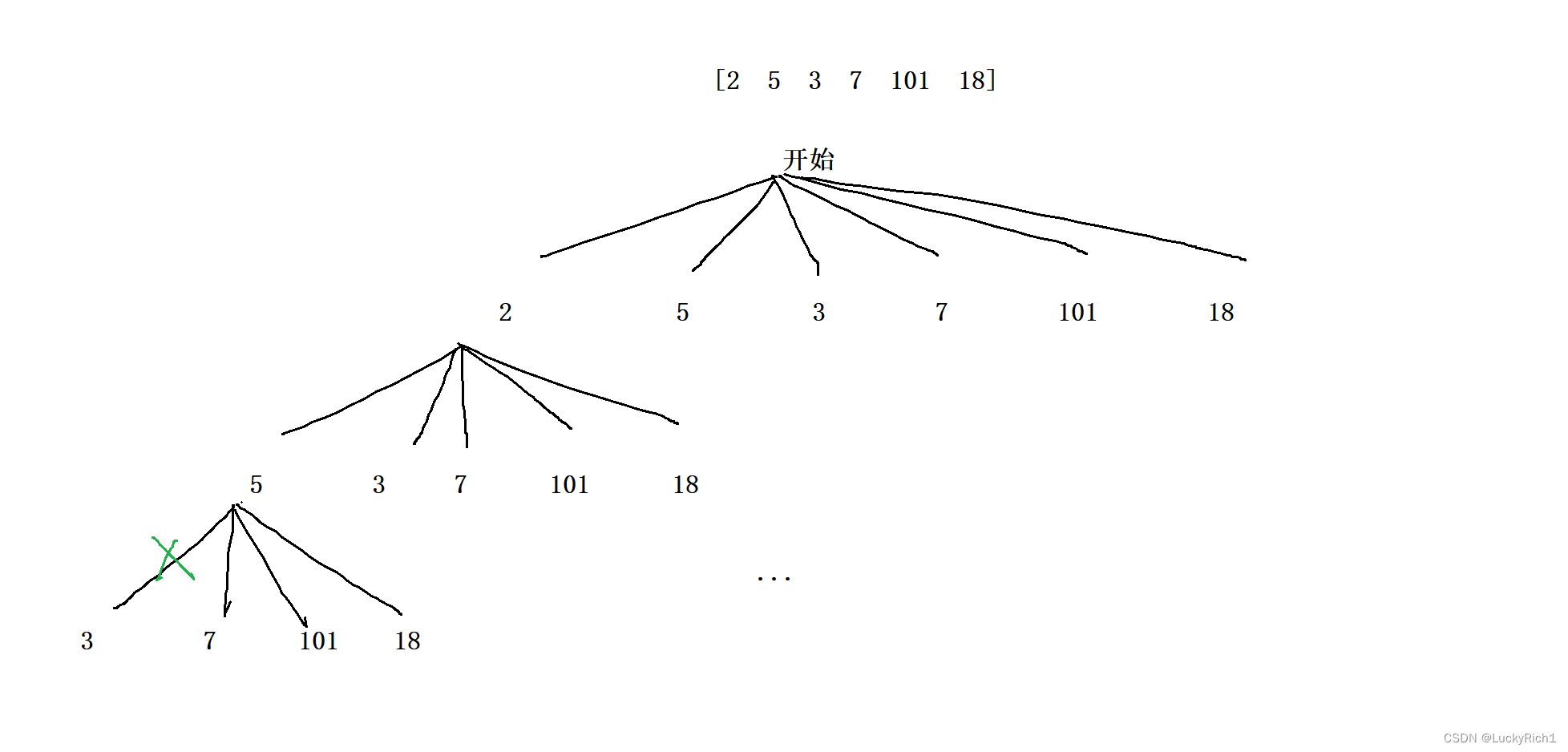
会超时间限制
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n=nums.size();
int ret=0;
for(int i = 0; i < n; ++i)
{
ret=max(ret,dfs(nums,i));
}
return ret;
}
int dfs(vector<int>& nums, int pos)
{
int ret=1;//必须等于1,如果pos是最后一个,循环进不去,但它也是一个子序列,返回1才对.
for(int i = pos + 1; i < nums.size(); ++i)
{
if(nums[i] > nums[pos])
ret=max(ret,dfs(nums,i)+1);
}
return ret;
}
};
暴搜->记忆化搜索
存在大量完全相同的问题,可以改成记忆化搜索
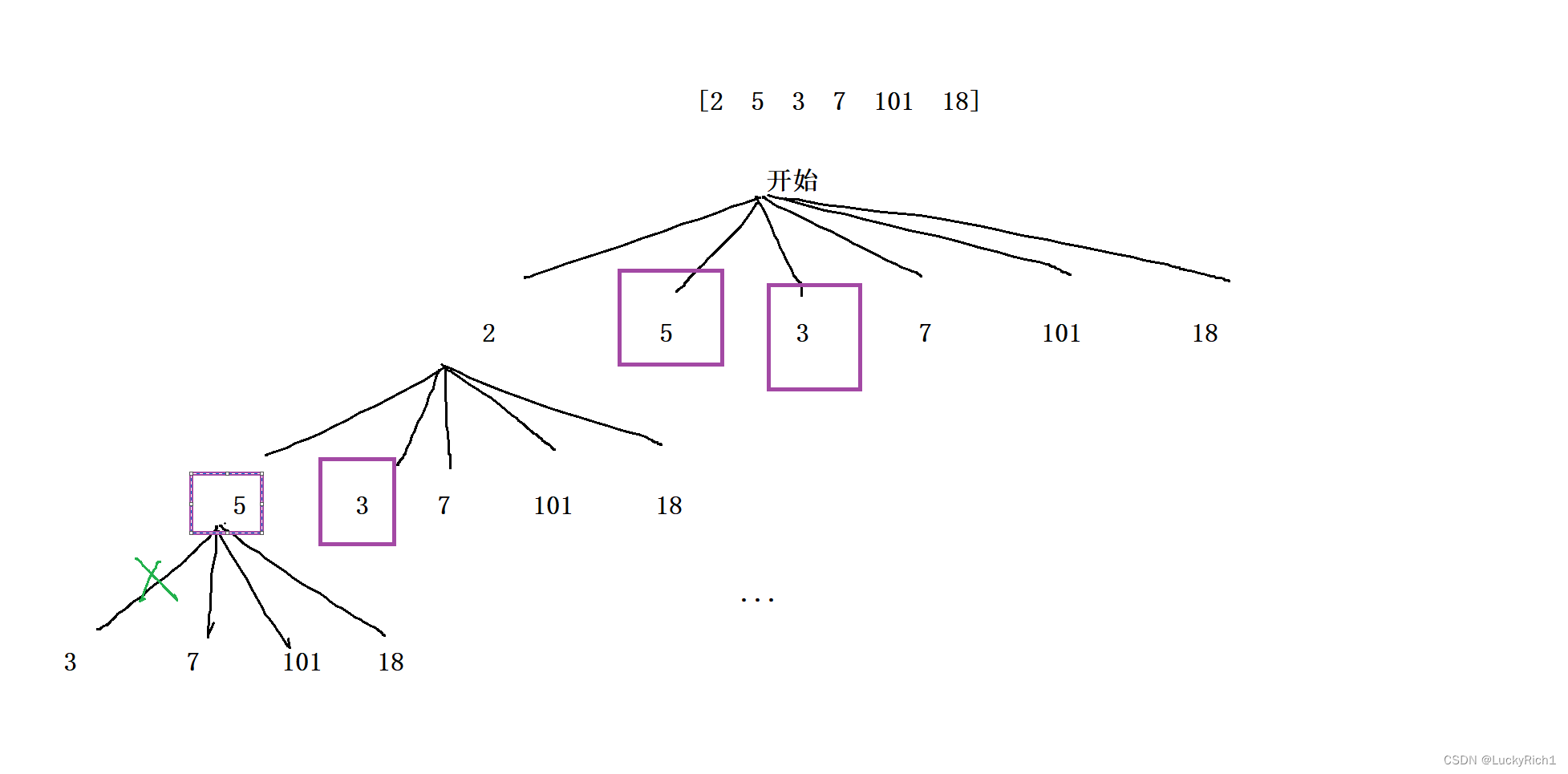
还是那三步,这里就不写了。这里备忘录用的是局部的也是可以的。
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n=nums.size();
vector<int> memo(n);
int ret=0;
for(int i = 0; i < n; ++i)
{
ret=max(ret,dfs(nums,i,memo));
}
return ret;
}
int dfs(vector<int>& nums, int pos, vector<int>& memo)
{
if(memo[pos] != 0) return memo[pos];
int ret=1;//必须等于1,如果pos是最后一个,循环进不去,但它也是一个子序列,返回1才对.
for(int i = pos + 1; i < nums.size(); ++i)
{
if(nums[i] > nums[pos])
ret=max(ret,dfs(nums,i,memo)+1);
}
memo[pos]=ret;
return ret;
}
};
记忆化搜索->动态规划
这里动态规划代码和之前的有点不一样。
首先来一个dp表,dfs函数->状态表示:dp[i]表示以i位置为起点的最长递增子序列长度。函数体-> 状态转移方程 :当求pos这个位置的时候,依赖的是pos后面的值,从里面找到最大然后在加+1。因此这个dp表填表顺序其实是从后往前填表。初始化都为1,自己本身也是一个子序列。返回值 返回的是dp表中最大值。
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
// 动态规划
int n=nums.size();
int ret=0;
vector<int> dp(n,1); //dp表+初始化
//填表顺序: 从后往前
for(int i = n-1; i >= 0; --i)
{
for(int j = i + 1; j < n; ++j)
{
if(nums[j] > nums[i])
{
dp[i]=max(dp[i],dp[j]+1);
}
}
ret = max(ret,dp[i]);
}
return ret;
}
};
4. 猜数字大小 II
题目链接: 375. 猜数字大小 II
题目分析:
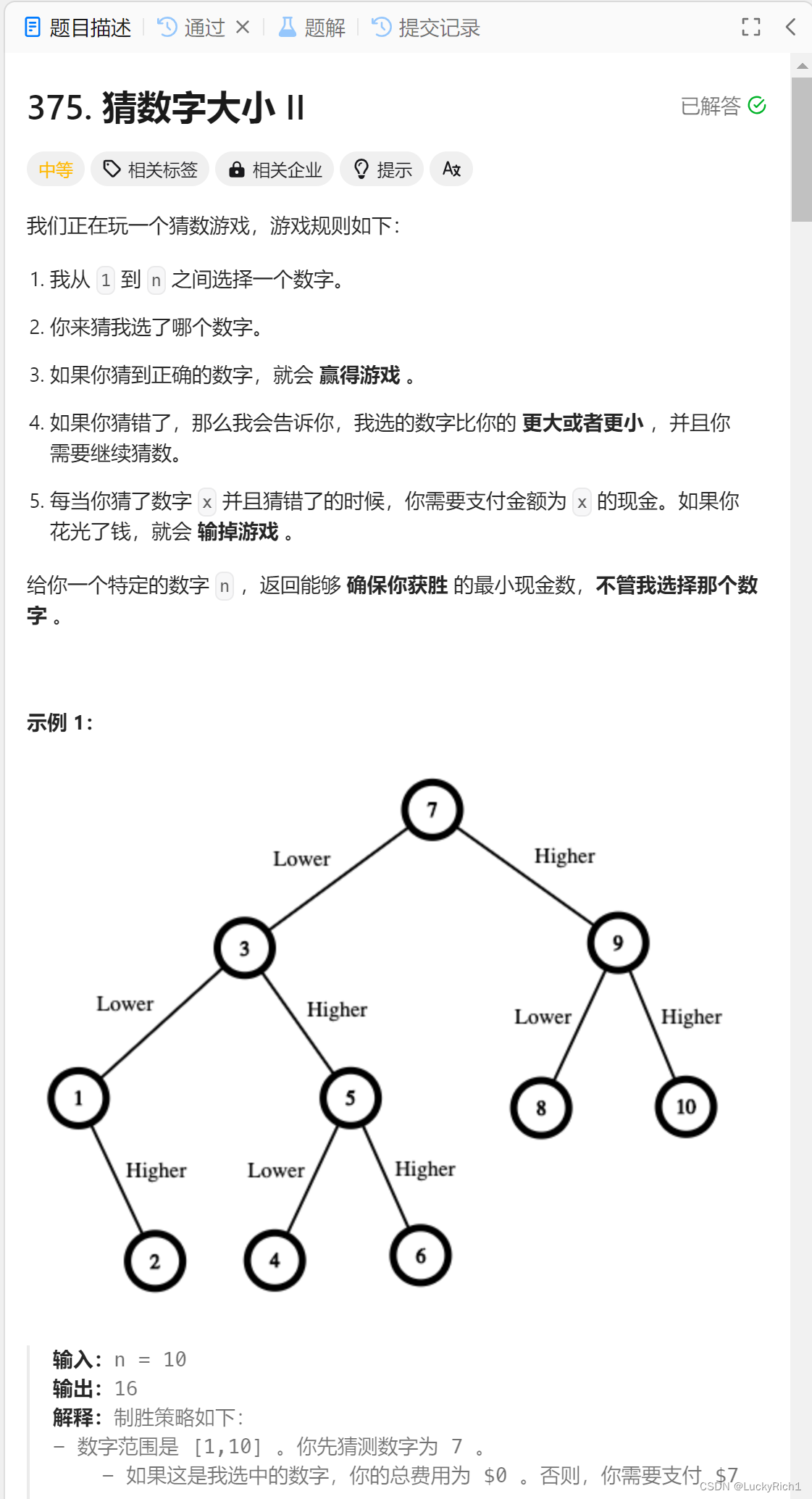
从1到n中间选择一个数字,然后猜选的是几。猜到正确就会赢得游戏,猜错了会告诉你选择数字比你大还是比你小,然后继续猜。如果到这里结束以前的二分查找就可以了。但是还有条件。每当猜一个数字如果猜错了是要支付费用的,费用是本次猜错的数字。如果花光钱还没有猜中就会输掉游戏。然后要求的是,给一个数字n,不管选择的是n中的那一个数字,都必须保证你要能猜对并且花的钱还要最少!
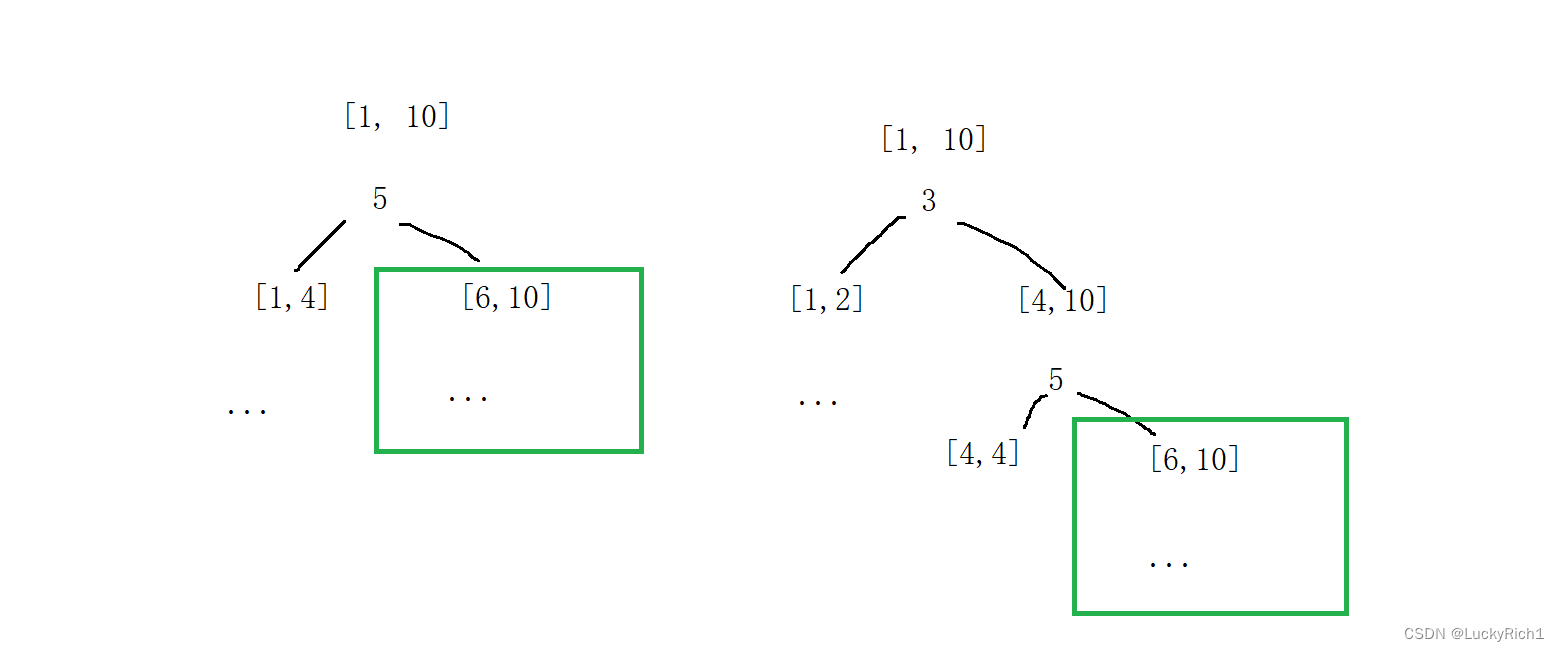
最左边这幅图如果选10只要16块钱,因为到9了还说比9大仅需把9支付下来就行了,10是不用支付的,并且这个16块钱不仅能够保证到右边还能保证到左边所有数字。中间这幅图如果被猜的数字是10就必须保证21块钱,并且这21能够到达所有数字。同理最右边的图也一样。总之有很多种选择,但是一定要选择钱用的最少的。大家会发现这是一个暴搜,把所有情况都枚举出来然后把最少的钱返回去。
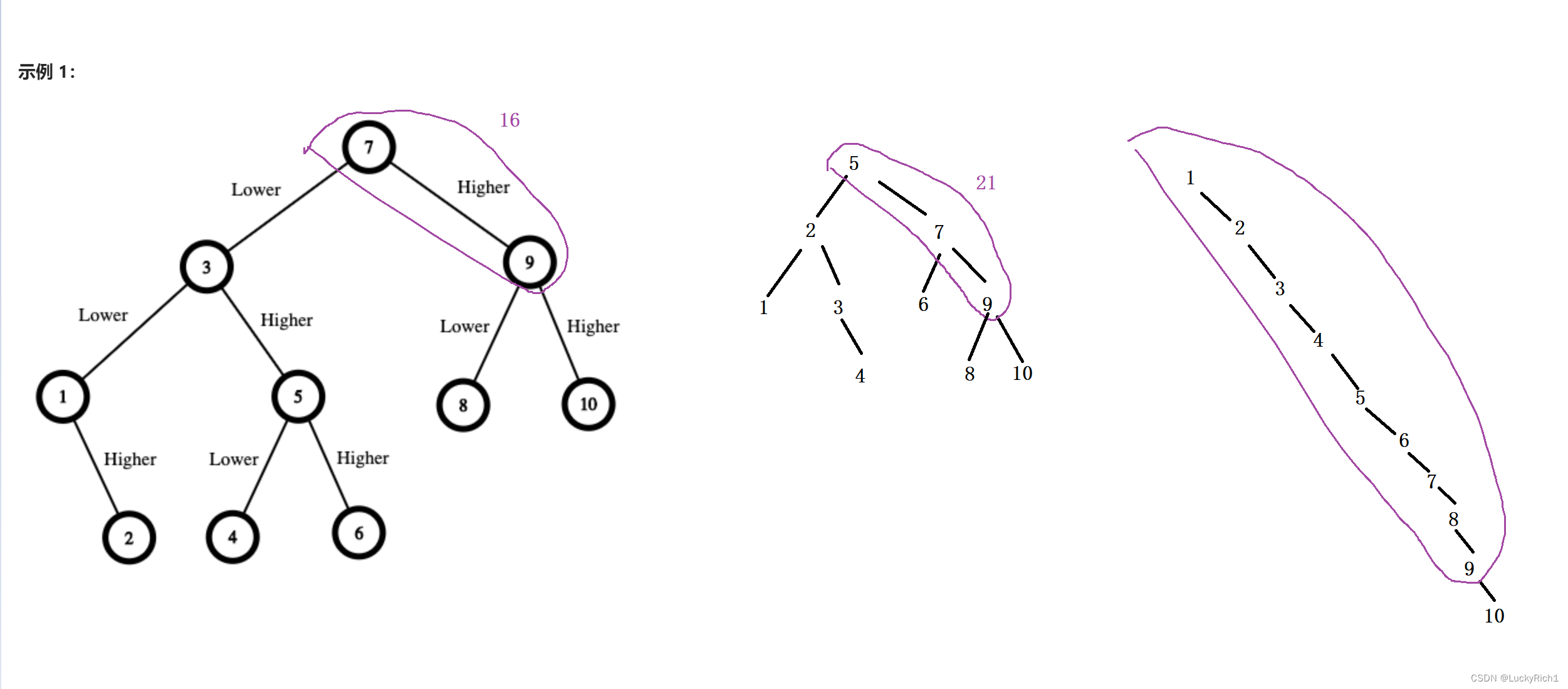
算法原理:
暴搜
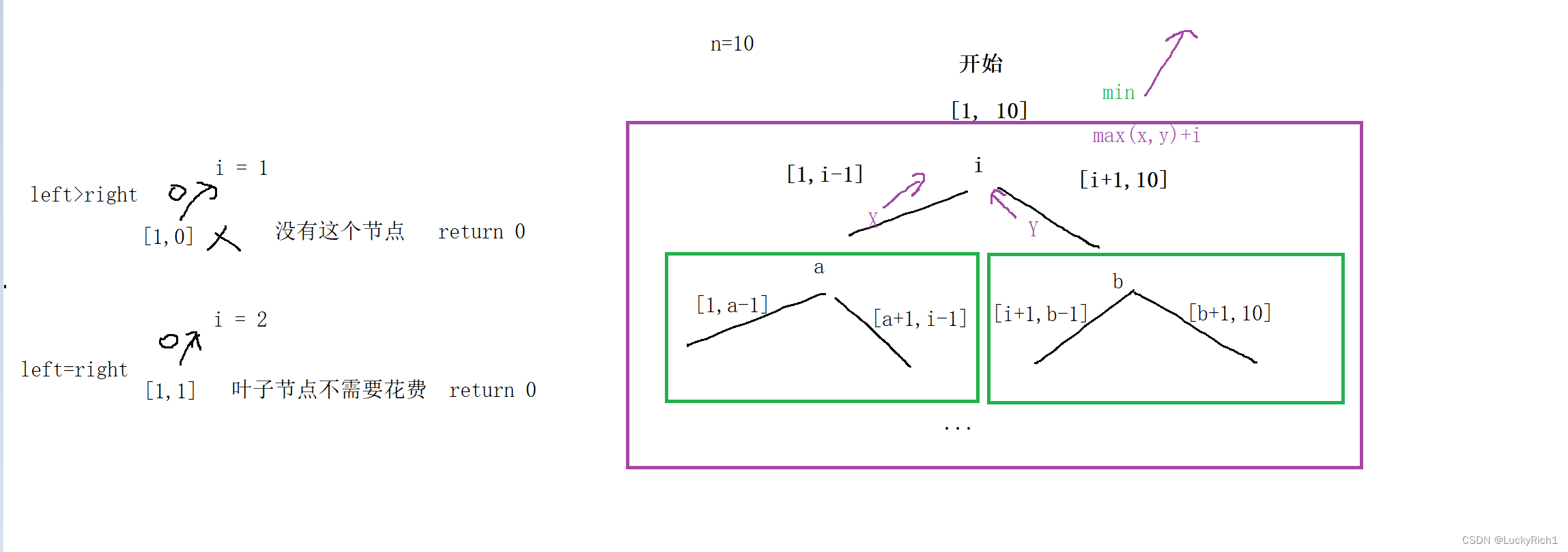
假设n=10,刚开始我要选择第一个数,第一个数可以从[1,10]中任选一个数i做头结点。接下来会告诉你这个数选大了还是小了,然后就可以去左子树和右子树去选。然后重复的就来了,左子树去[1,i-1]任选一个a做头节点然后处理左子树右子树,右子树去[i+1,10]任选一个b做头节点然后处理左子树右子树。重复情况就是给我一个区间,我给你选一个头然后处理一下左子树和右子树。在所有的头i,注意i是在[1,10]变化的然后向上返回一个最小值。
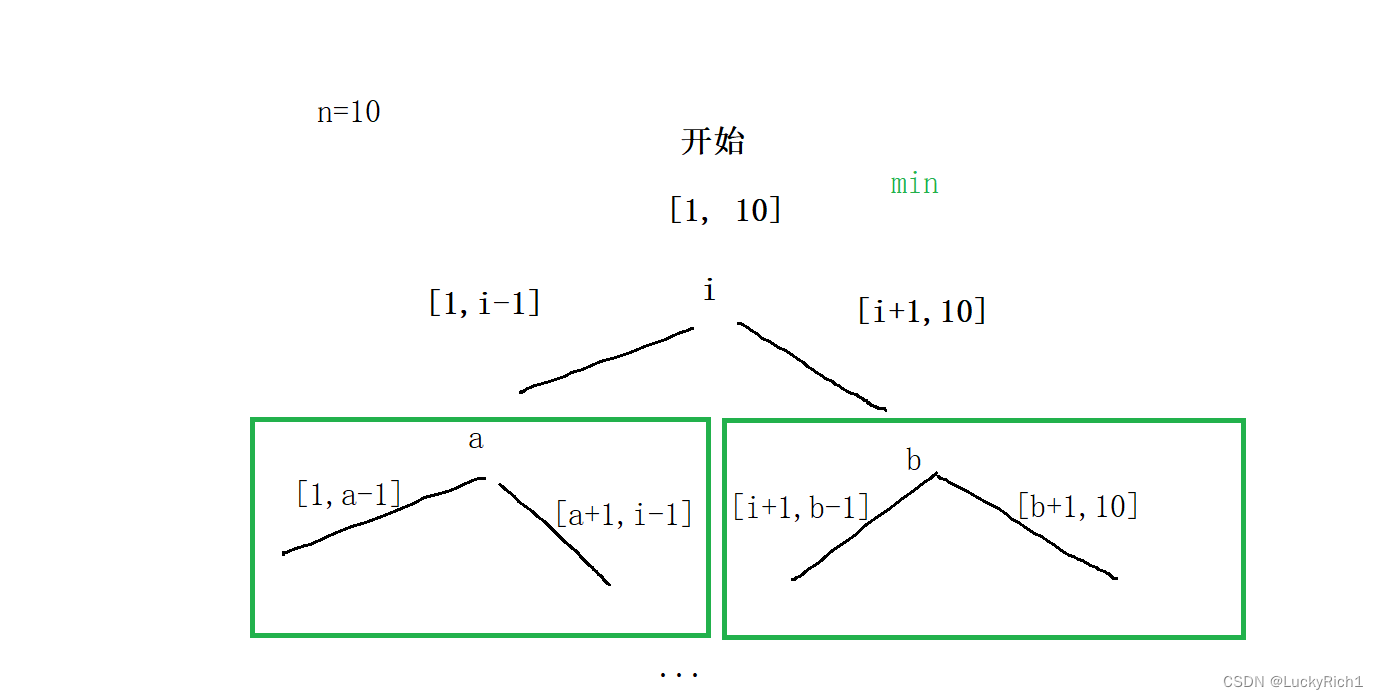
接下来我们在细细看一下,当以i为根节点的时候处理完左子树和右子树,左右子树分别给我返回一个值假设是x和y。x代表左子树所有情况中最小值,y代表右子树所有情况中最小值。当在i的位置拿到x和y的时候,此时我要的是x和y中的最大值!因为要保证左右子树都能完胜,所以拿到左右子树中最大值那样左右子树都能完胜,然后还要在加上当前选的i自己本身。当把所有以i为根节点的情况都拿到了在取其中最小值就可以了。
因此dfs函数这样设计,给一个区间,然后把这个区间的保证胜利的最小值返回去。int dfs(1,10) ,函数体 从1到10枚举头结点,然后dfs枚举头结点的左区间和右区间,然后两者之间最大值然后加上i。然后把i=1、i=2。。。所有情况中取最小值,向上返回。递归出口 有两个递归出口,当left>=right。
class Solution {
public:
int getMoneyAmount(int n) {
return dfs(1,n);
}
int dfs(int left, int right)
{
if(left >= right) return 0;//区间越界和碰到叶子节点
int ret = INT_MAX;
for(int head = left; head <= right; ++head)
{
int l = dfs(left,head-1);
int r = dfs(head+1, right);
ret = min(ret, max(l,r)+head);
}
return ret;
}
};
暴搜->记忆化搜索
递归过程出现大量完全相同的问题,可以改成记忆化搜索
class Solution {
int memo[201][201];
public:
int getMoneyAmount(int n) {
return dfs(1,n);
}
int dfs(int left, int right)
{
if(left >= right) return 0;
if(memo[left][right] != 0) return memo[left][right];
int ret = INT_MAX;
for(int head = left; head <= right; ++head)
{
int l = dfs(left,head-1);
int r = dfs(head+1, right);
ret = min(ret, max(l,r)+head);
}
memo[left][right]=ret;
return ret;
}
};
5.矩阵中的最长递增路径
题目链接: 329. 矩阵中的最长递增路径
题目分析:

给一个mxn的矩阵,里面有很多递增序列,返回里面递增序列的最长长度。
算法原理:
暴搜
让找最长递增序列长度,那就暴力枚举所有递增序列从中选择最长的。从第一个位置开始走,上下左右去找,然后返回这个位置上下左右中最长的,记住还要加自己本身1个。比如从1开始有2和6两种走法,从6返回的是2加起点最长递增是4,从2返回的是3加起来最长递增长度是4,所有1这个位置最长递增是4。然后还要和其他位置比,选择最长的。

class Solution {
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int m,n;
public:
int longestIncreasingPath(vector<vector<int>>& matrix) {
m=matrix.size(),n=matrix[0].size();
int ret=0;
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; ++j)
{
ret = max(ret,dfs(matrix, i, j));
}
}
return ret;
}
int dfs(vector<vector<int>>& matrix, int i, int j)
{
int ret = 1;
for(int k = 0; k < 4; ++k)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j])
{
ret = max(ret, dfs(matrix, x, y)+1);
}
}
return ret;
}
};
暴搜->记忆化搜索
从1到6搜索和从6开始搜索情况是一样的。因此可以改成记忆化搜索。
class Solution {
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int m,n;
int memo[201][201];
public:
int longestIncreasingPath(vector<vector<int>>& matrix) {
memset(memo, -1, sizeof memo);
m=matrix.size(),n=matrix[0].size();
int ret=0;
for(int i = 0; i < m; ++i)
{
for(int j = 0; j < n; ++j)
{
ret = max(ret,dfs(matrix, i, j));
}
}
return ret;
}
int dfs(vector<vector<int>>& matrix, int i, int j)
{
if(memo[i][j] != -1) return memo[i][j];
int ret = 1;
for(int k = 0; k < 4; ++k)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j])
{
ret = max(ret, dfs(matrix, x, y)+1);
}
}
memo[i][j]=ret;
return ret;
}
};





![[图解]企业应用架构模式2024新译本讲解18-活动记录2](https://img-blog.csdnimg.cn/direct/7ba1eb77768d4f85ad7b2c48f0a5b437.png)