目录

1.相关概念

（1）什么是树

（2）生成树和最小生成树：

2.适用赛题

（1）赛题分类

（2）不同之处

3.两种算法

（1）prim算法

（2）Kruskal算法

4.典型赛题

（1）架设通信线路

（2）Matlab代码分析

（3）运行结果

（4）代码分享

---

1.相关概念

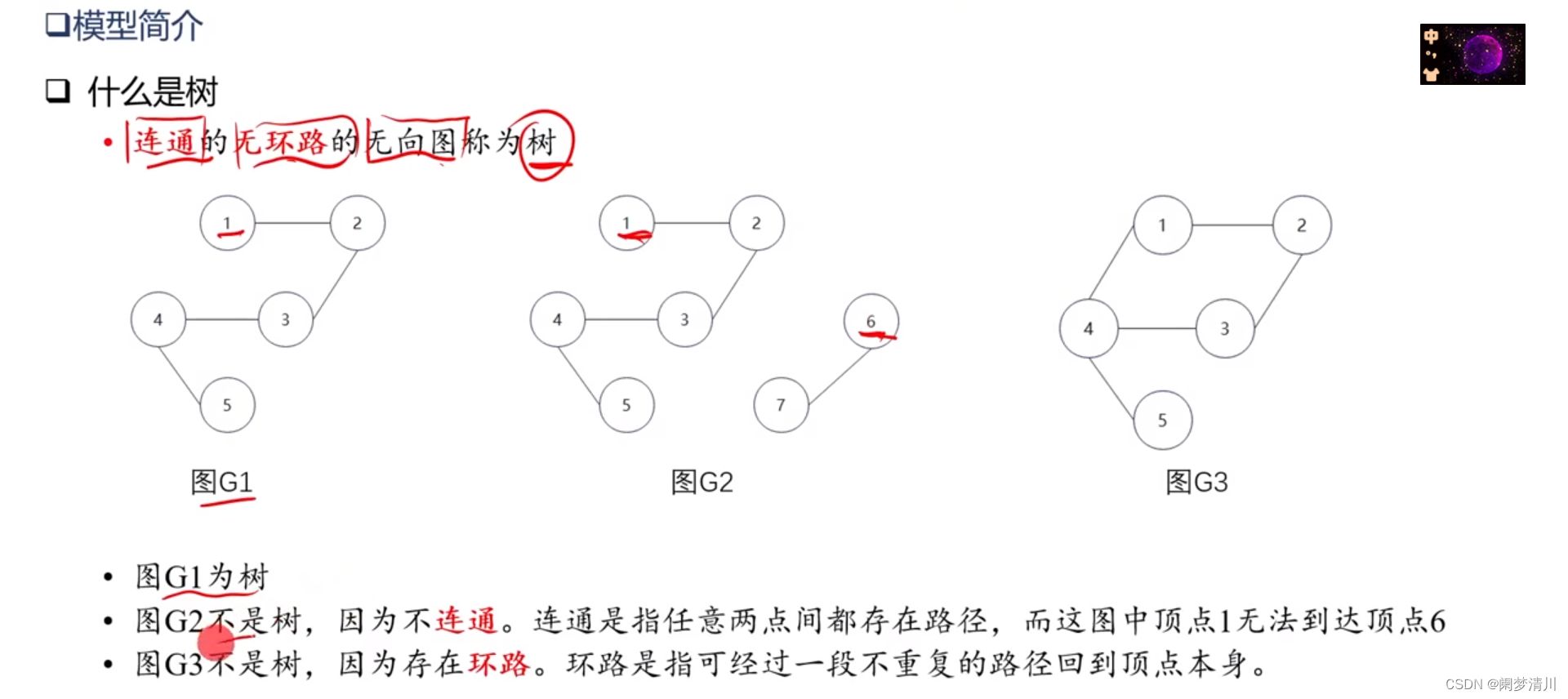
（1）什么是树

连通，无环路，无向图就是树；

（2）生成树和最小生成树：

生成树就是一个图的子图，而且是一个树，包括原来的图的所有的顶点，一个图可能会有多个生成树，可能会有多个最小生成树，但是最小生成树的长度是唯一的；

2.适用赛题

（1）赛题分类

通信建设问题，以及这个管道的铺设问题，都是这类最小生成树问题，求解的就是这个通信线路的最短情况和这个铺设管道最节省的情况；

（2）不同之处

这个不同之处指的就是这个最小生成树和最短路径的不同之处，这个最小生成树里面没有指定这个起点和终点，只要求能够把所有的顶点走一遍就可以了；

而最短路径是指明了起点和终点，在这个限制条件下要求这个路径最短，这个是否指定起点和终点是这两个问题的本质区别；

3.两种算法

因为这个无论是在数据结构里面，还是在离散数学里面，这个算法我们都已经学习了解过了，因此下面我不会进行详细的赘述；

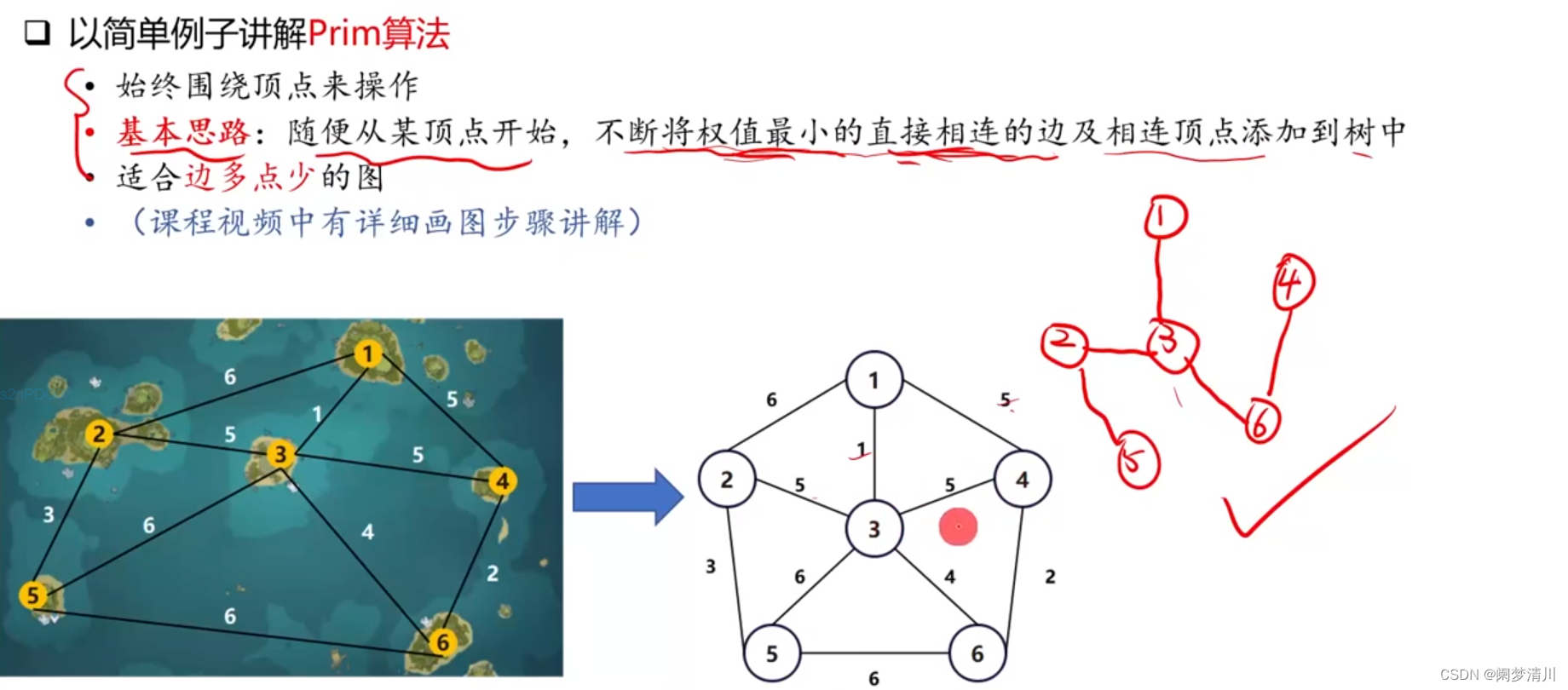
（1）prim算法

（2）Kruskal算法

4.典型赛题

（1）架设通信线路

（2）Matlab代码分析

我们首先要生成一个邻接矩阵，然后再根据这个不同的顶点之间的长度去初始化这个不同位置的元素的数值；

我们现实生成了一个9*9的全是0的矩阵，然后就是根据不同顶点之间的权重去对于这个矩阵的相应的位置进行初始化；这个地方需要注意的是这个生成树是没有方向的，我们对于两个顶点之间的边，只需要初始化一次；

例如1,2这两个顶点之间，权重是2，我们在对于和1相关联的节点初始化之后，就已经把和1节点相关联的2节点给初始化了；当我们对于这个2节点及其相关联的边进行初始化的时候，这个就不需要重复的进行初始化操作；

upper是指使用的是这个矩阵的上三角，因为如果全部使用就会把每两个顶点之间出现两条边，这个最小生成树是无向图，我们只需要使用上三角即可；

这个里面使用到的相关函数的简单介绍我放到下面了： 

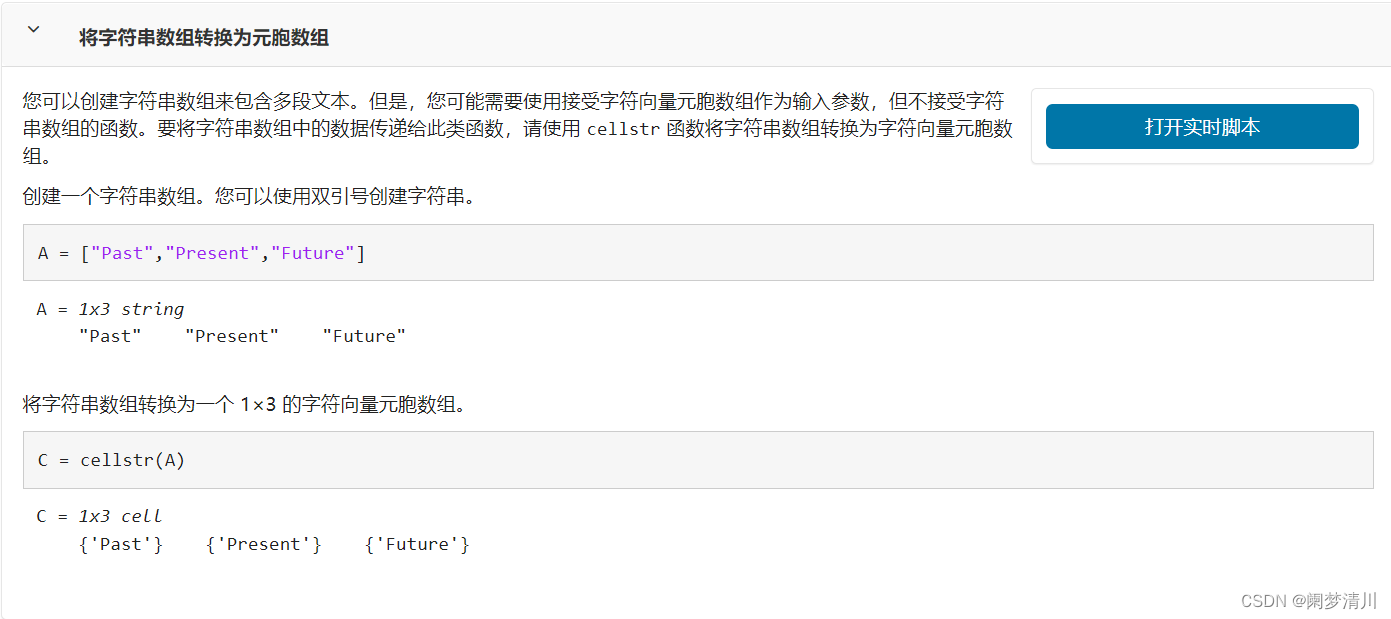
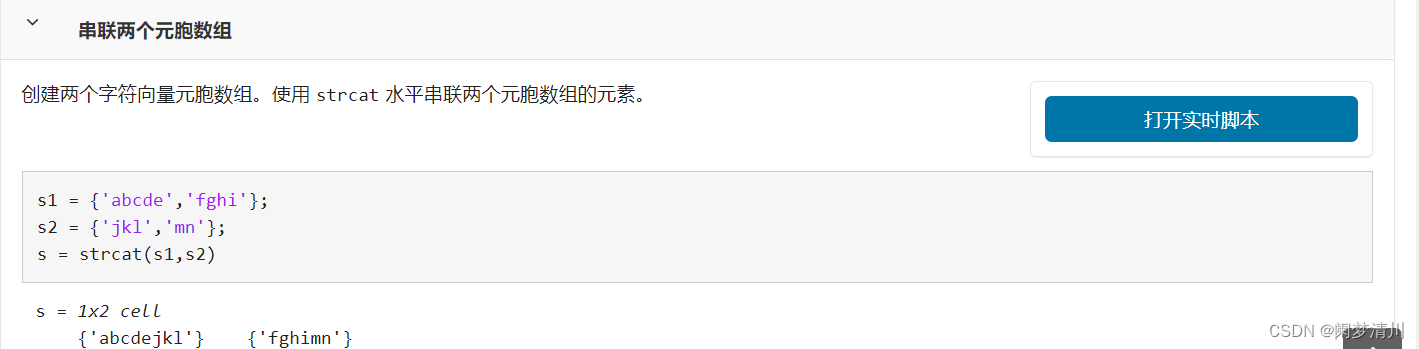
 接下来就是求解最小生成树，sparse表示使用的是地杰斯特算法，这个是我们自己设置的，不进行设置的话就会使用默认的prim算法，这两个都是可以进行求解的，只是这个效率上面可能会有区别，读者可以下去进行尝试；

L=sum就是对于这个权重求和，求解得到这个最小权重和，highlight是对于这个图形的优化；

（3）运行结果

最小权重和是47，这个最小生成树如图所示：

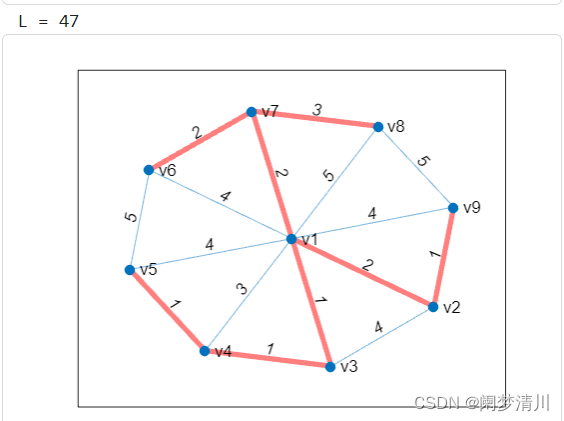
（4）代码分享

clear,clc;

a=zeros(9);
a(1,[2:9])=[2 1 3 4 4 2 5 4];
a(2,[3 9])=[4 1];
a(3,4)=1;
a(4,5)=1;
a(5,6)=5;
a(6,7)=2;
a(7,8)=3;
a(8,9)=5;

s=cellstr(strcat('v',int2str([1:9]')));

G=graph(a,s,'upper');%使用上三角矩阵画出图形

p=plot(G,'EdgeLabel',G.Edges.Weight);



T=minspantree(G,'Method','sparse');%使用迪杰斯特算法

L=sum(G.Edges.Weight)

highlight(p,T,'EdgeColor','Red','LineWidth',2.5)