【算法专题--栈】后缀表达式求值 -- 高频面试题（图文详解，小白一看就会！！）

news2024/10/7 10:13:24

一、前言

二、题目描述

三、解题方法

⭐解题思路

⭐案例图解

四、总结与提炼

五、共勉

一、前言

后缀表达式求值 这道题，可以说是--栈专题--，最经典的一道题，也是在面试中频率最高的一道题目，通常在面试中，面试官可能会从多个方面考察这道题目，所以大家需要对这道题目非常熟悉哦！！
本片博客就来详细的讲讲解一下 后缀表达式求值 的实现方法，让我们的面试变的更加顺利！！！

二、题目描述

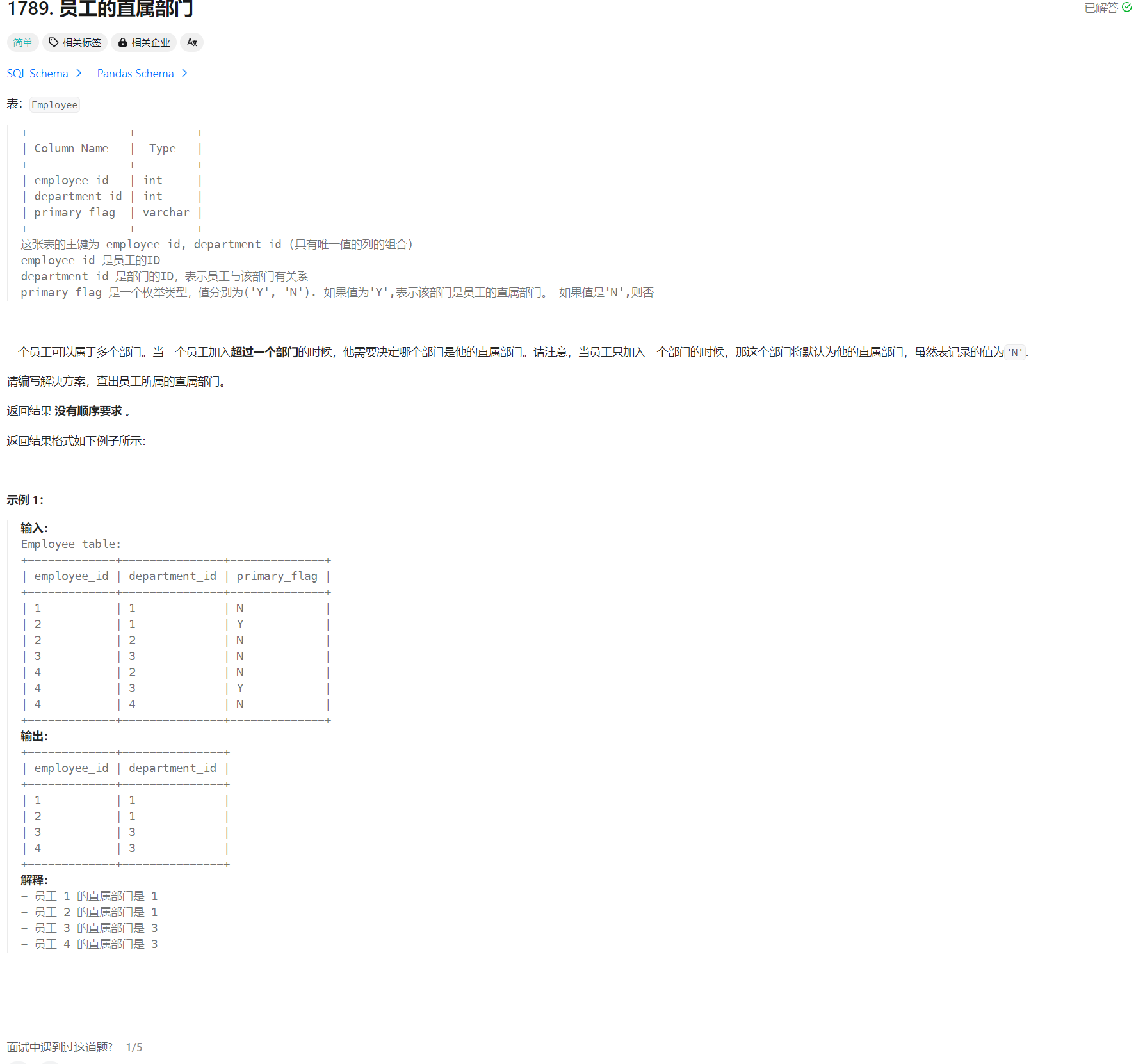
题目链接： 150. 逆波兰表达式求值 - 力扣（LeetCode）

给你一个字符串数组 tokens ，表示一个根据逆波兰表示法表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

三、解题方法

⭐解题思路

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果
适合用栈操作运算：遇到数字则入栈；遇到运算符则取出栈顶两个数字进行计算，并将结果压入栈中

方法 --- 栈

定义一个栈 stk，栈中存放 int 整型数字。遍历字符串数组：

遇到数字字符将数字字符转化成 int 整型数字存放在栈中；
遇到运算符，就将栈顶两个数字出栈，执行相应的运算符操作。

我们在遍历字符串数组的时候，需要将字符型数字转化成整型数字，在 C++ 中有两种方法：

stoi()：将字符串型数字转化成整型数字；
atoi()：将字符型数字转化成整型数字。

⭐案例图解

后缀表达式： 【"2"，"1"，"+"，"3"，"*"】

遍历整个动态数组

将数字字符 转换为 数字整型 ，放入栈中

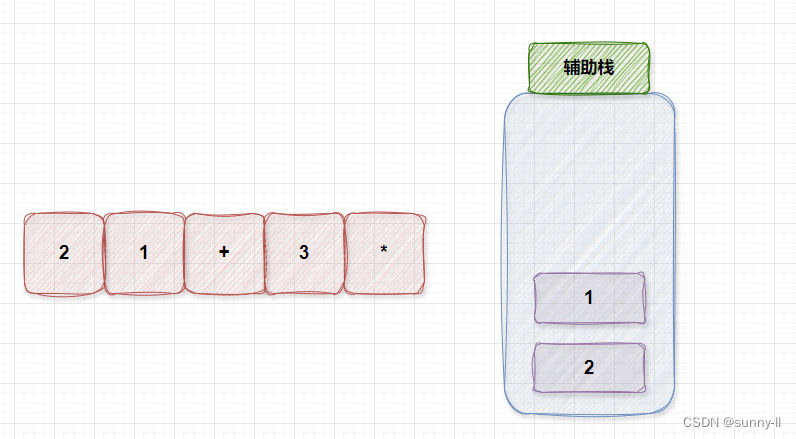
当遇到 运算符时，将栈顶的两个数字出栈，执行相应的运算符操作

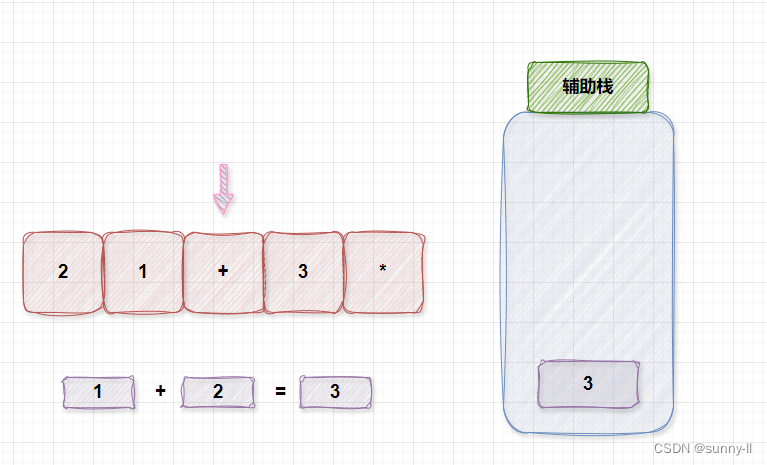
继续入栈，重复上述操作

最后返回栈顶【9】即可！

代码：

class Solution {
public:
    int evalRPN(vector<string>& tokens) 
    {
        stack<int> st;
        // 遍历整个 动态数组 vector<int>& tokens
        for(auto& e: tokens)
        {
            if(e == "+" || e == "-" || e == "*" || e == "/")
            {
                // 如果是操作符 就取栈顶 的前两个元素 作为左右操作数
                int right = st.top();
                st.pop();
                int left = st.top();
                st.pop();

                // switch 的括号里面必须是整形 ：int , char
               switch(e[0])
               {
                    case '+':
                        st.push(left+right);
                        break;
                    case '-':
                        st.push(left-right);
                        break;
                    case '*':
                        st.push(left*right);
                        break;
                    case '/':
                        st.push(left/right);
                        break;
               }
            }
            else
            {
                // 如是是 操作数 入栈
                st.push(stoi(e));  //将字符串 转 整形
            }
        }
        return st.top();
    }
};