目录
- 1. 准备工作
- 1.1 安装MySQL
- 1.2 验证MySQL的环境变量
- 2. 环境变量配置
- 3. 访问MySQL
- 3.1 命令行访问MySQL
- 3.2 Workbench访问MySQL
1. 准备工作
1.1 安装MySQL
如果您已经安装了MySQL,请从【2. Mysql 环境配置】开始;如果您没有安装MySQL,请参考【2024最新版】Mysql数据库安装全攻略:图文详解(Windows版本),进行安装。
1.2 验证MySQL的环境变量
在电脑菜单的搜索栏中输入cmd,选择【命令提示符】。
在【命令提示符】对话框中,输入下面内容:
mysql -u root -p
如果显示 “‘mysql’ 不是内部或外部命令,也不是可运行的程序或批处理文件。”,如下图:
则说明mysql没有配置环境变量,如果已经配置,则会显示版本号。
如果已经配置了环境变量,跳过【2. 环境变量配置】的内容即可。
2. 环境变量配置
在电脑搜索框中输入【系统】,在弹出框中选择【编辑系统环境变量】。
在【系统属性】弹出框中,选择【高级】Sheet,然后单击【环境变量】按钮。

在【环境变量】弹出框中,选择【Path】,单击【编辑】按钮。
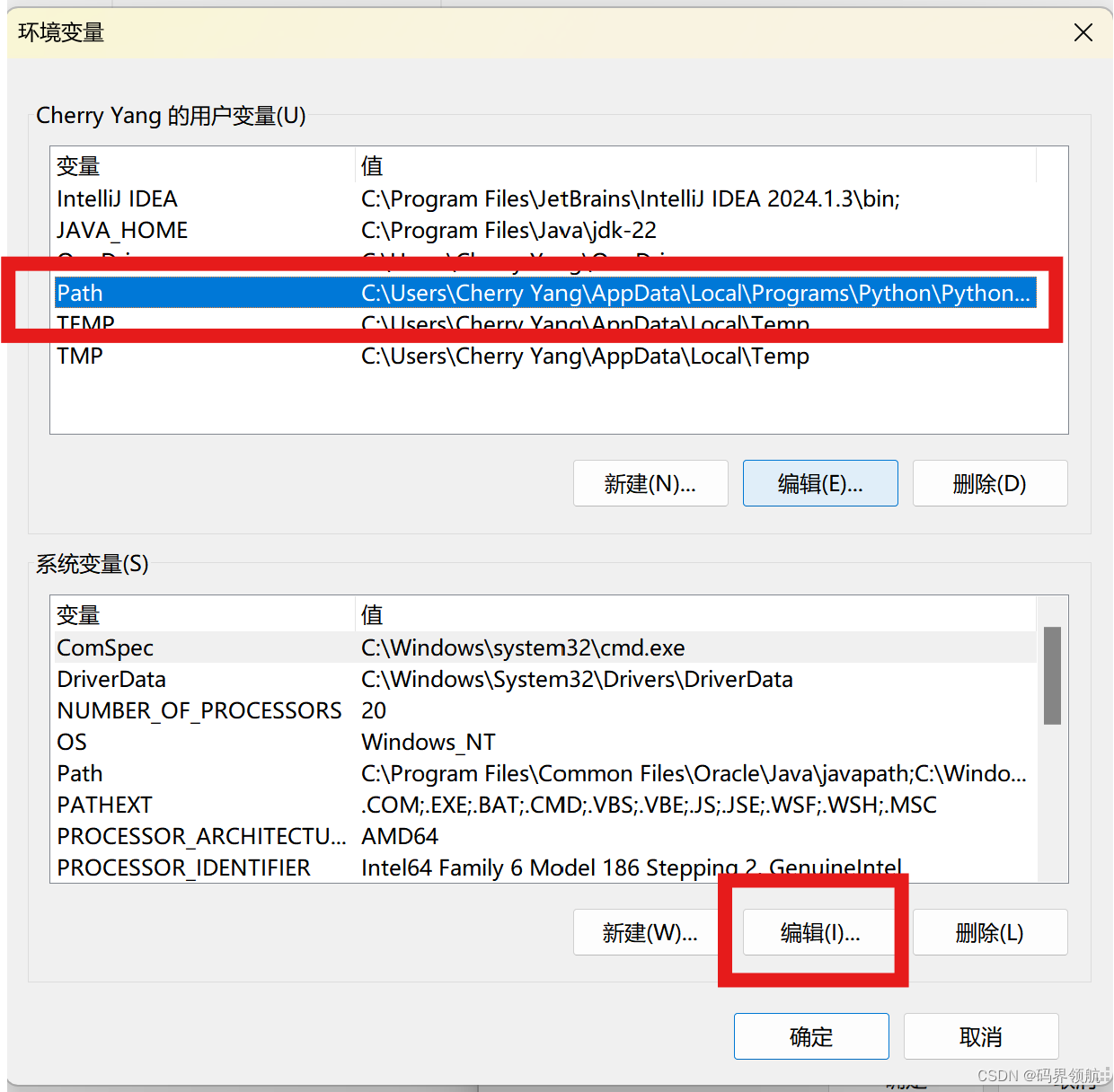
在【编辑环境变量】对话框中,选择【新建】,在内容中输入mysql安装路径下的bin目录的路径,这里使用的是默认安装路径(C:\Program Files\MySQL\MySQL Server 8.0\bin),然后单击【确定】按钮。
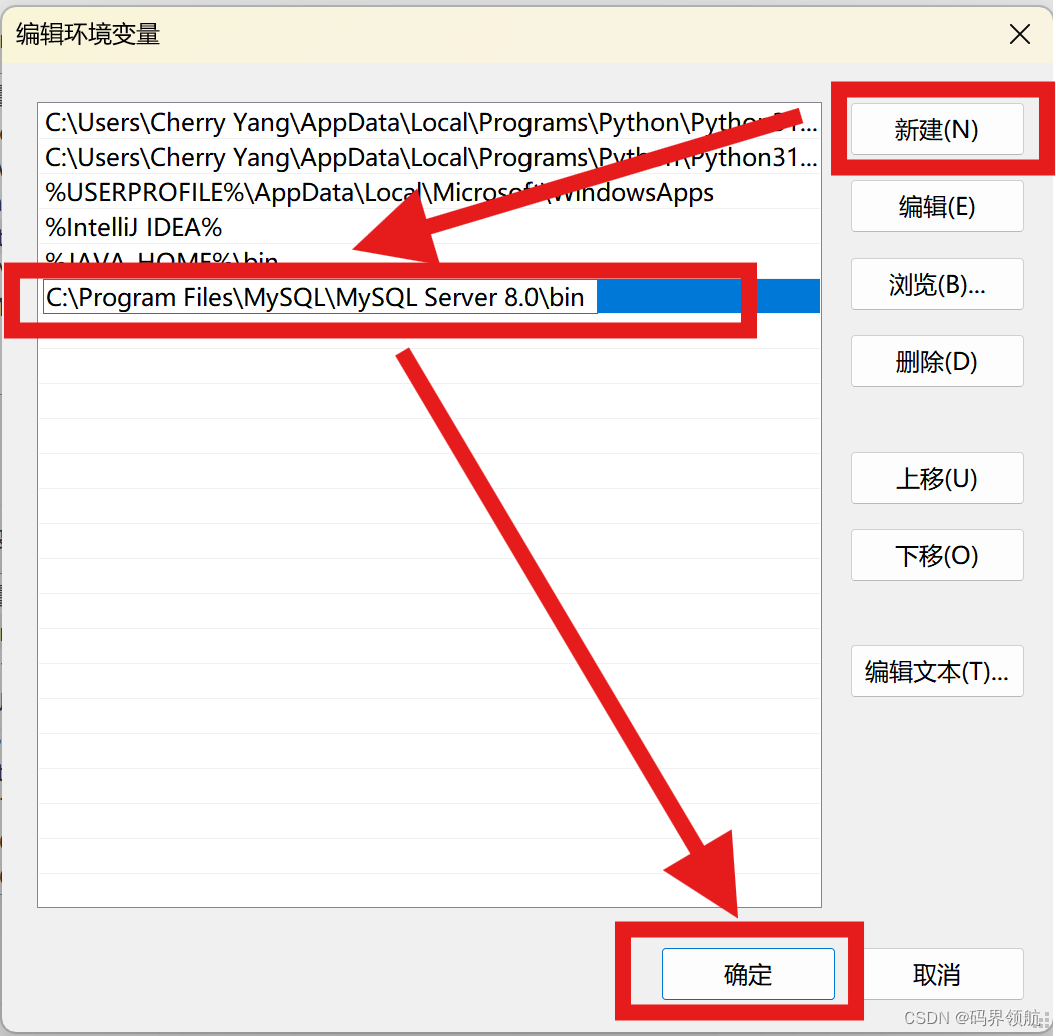
在【环境变量】对话框中,单击【确定】按钮。
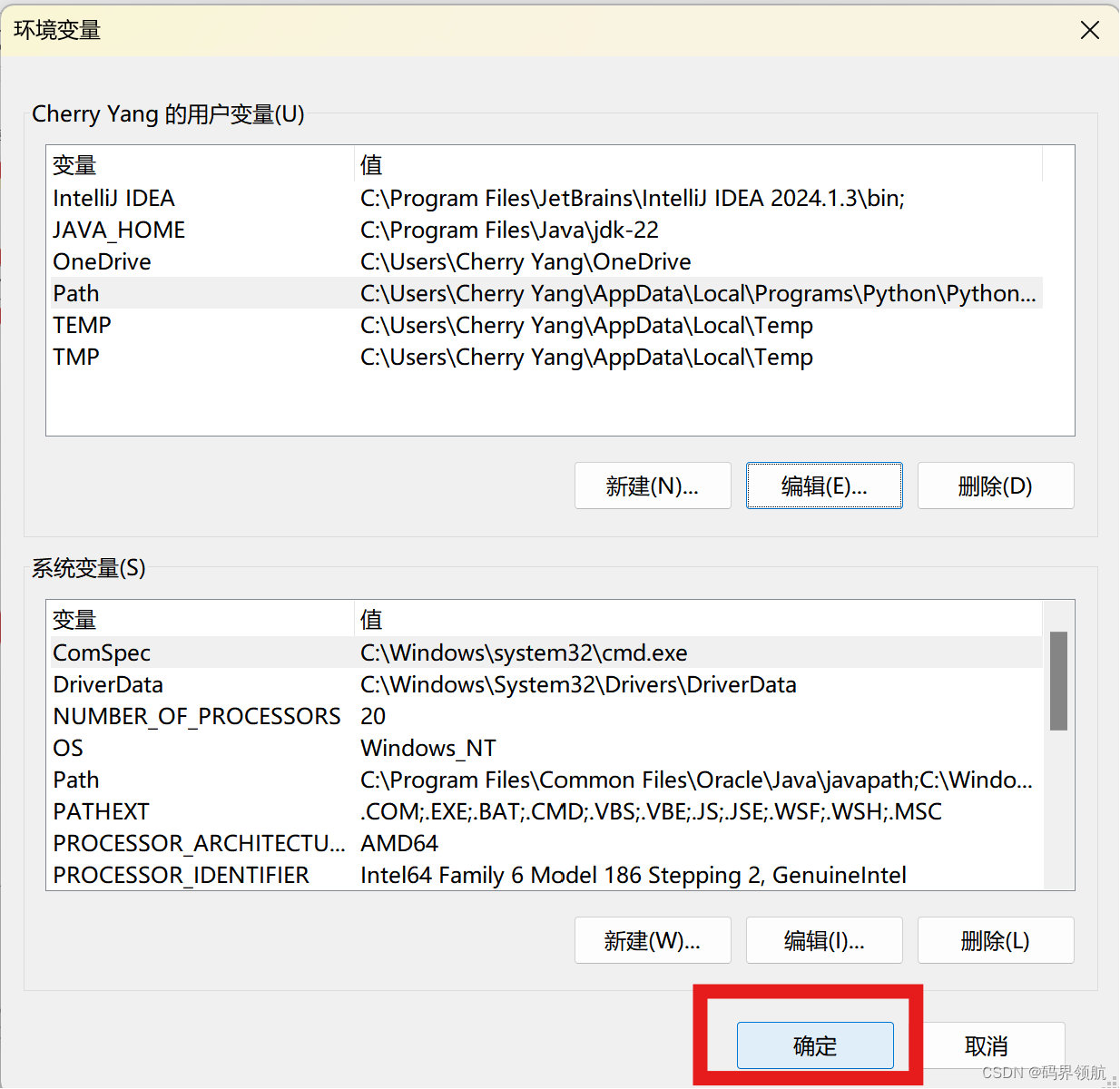
3. 访问MySQL
3.1 命令行访问MySQL
在计算机的菜单搜索栏中,输入cmd,选择【命令提示符】。
提示:如果之前已经打开命令提示符界面,这时需要关闭,重新打开。
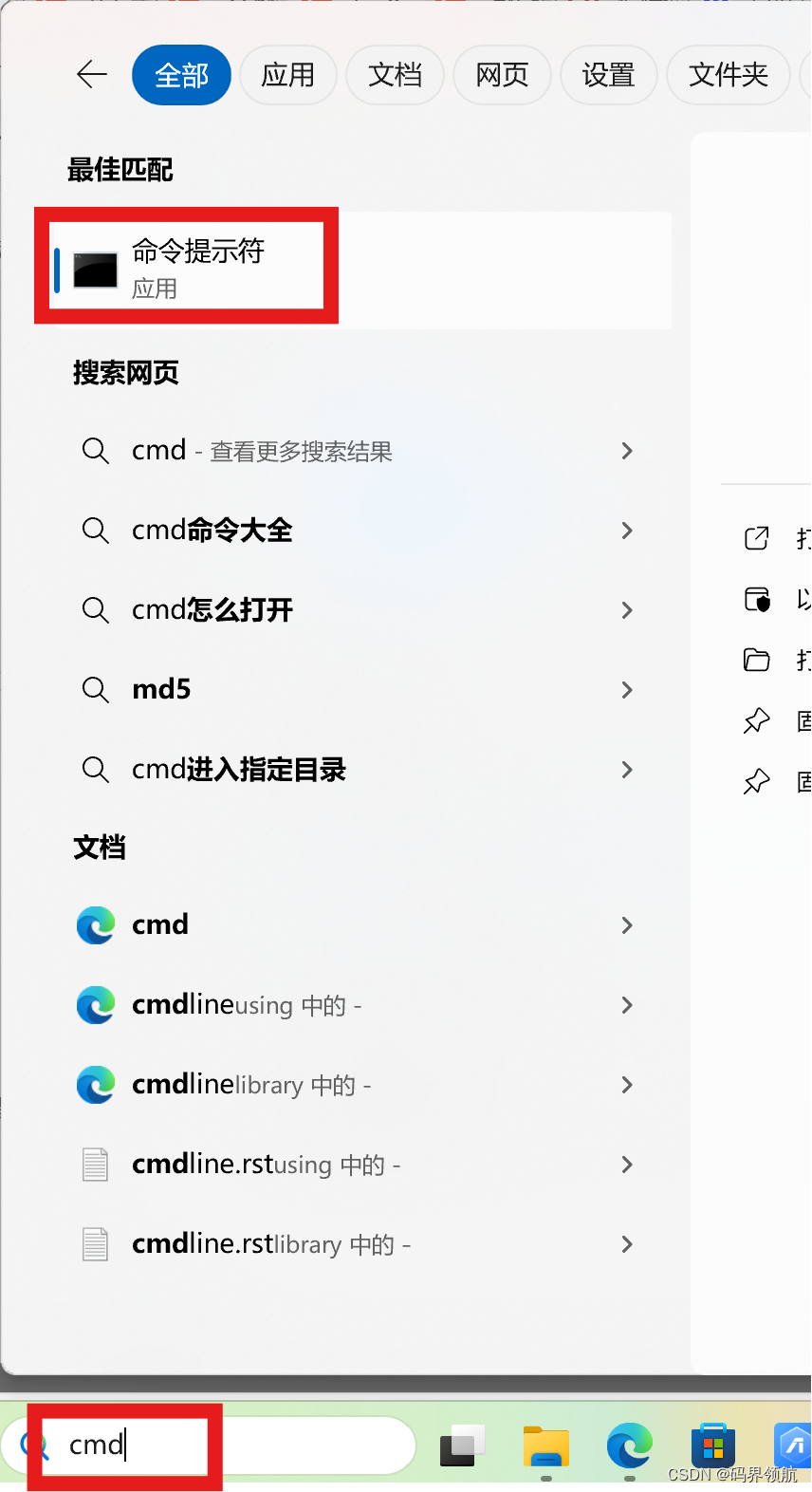
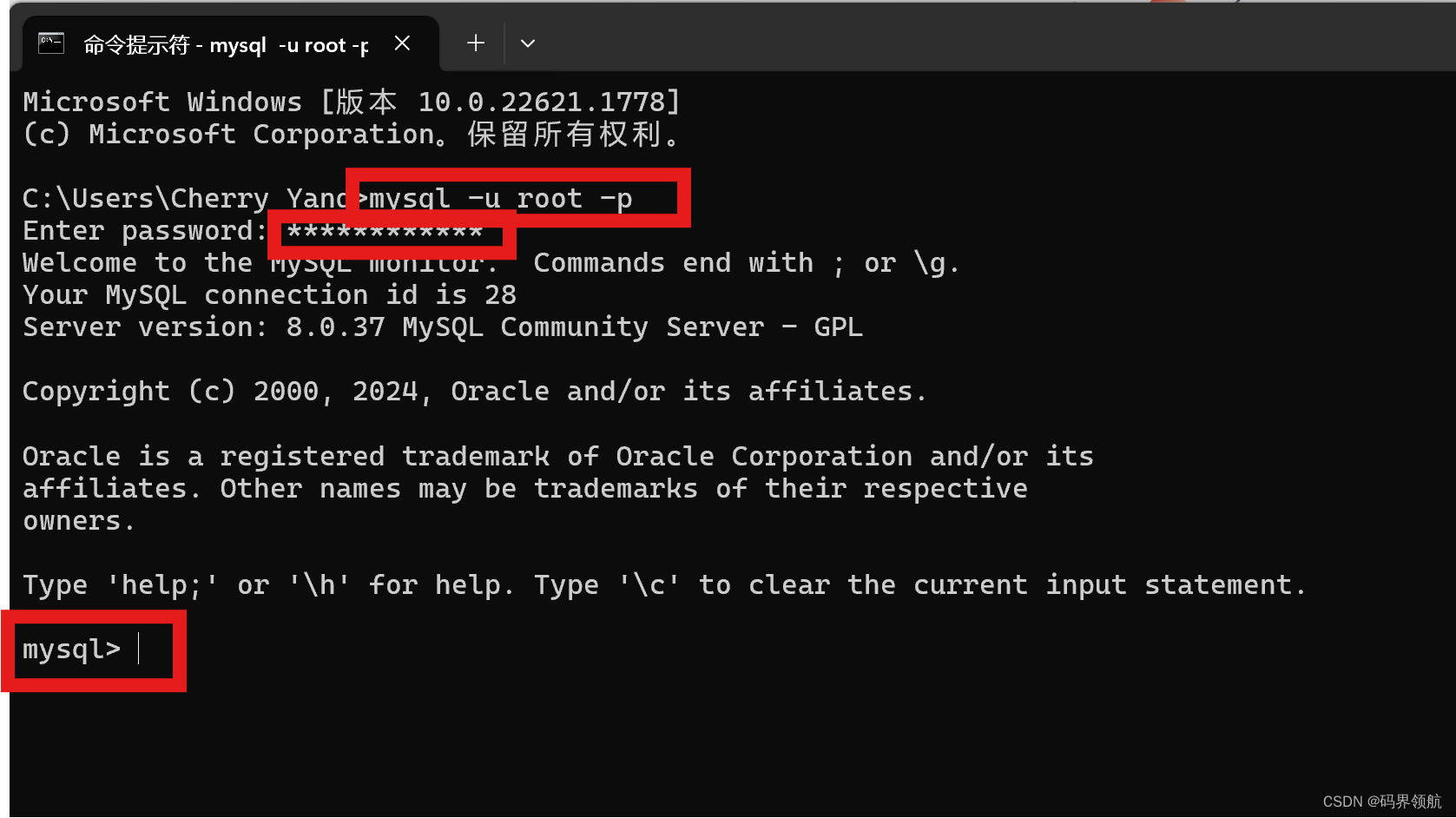
在【命令提示符】对话框中,输入下面内容:
mysql -u root -p
系统输出 “Enter password:”,输入安装mysql时设置的mysql密码,即可进入。
3.2 Workbench访问MySQL
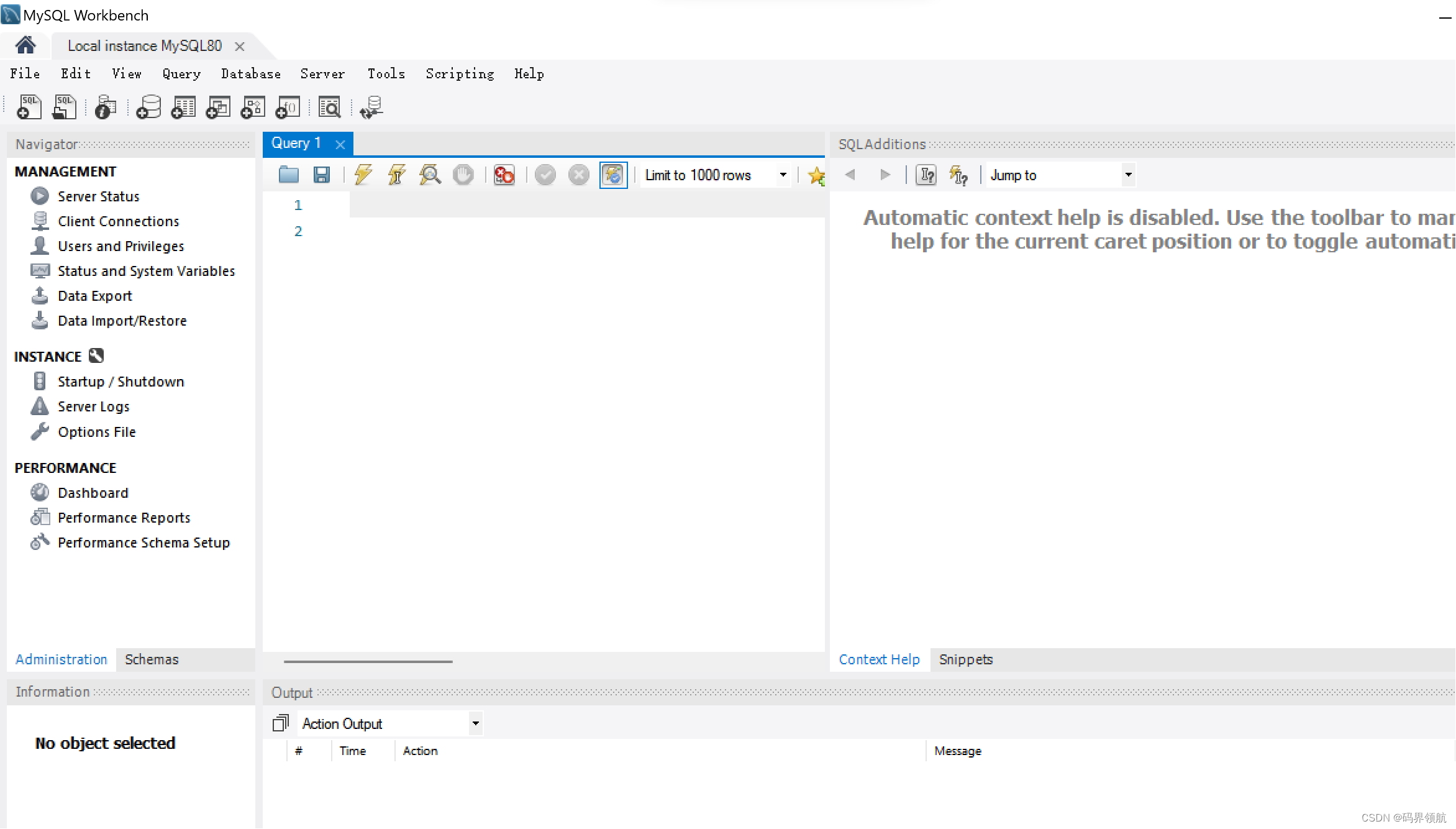
打开MySQL Workbench应用。

单击【local instance MySQL80】
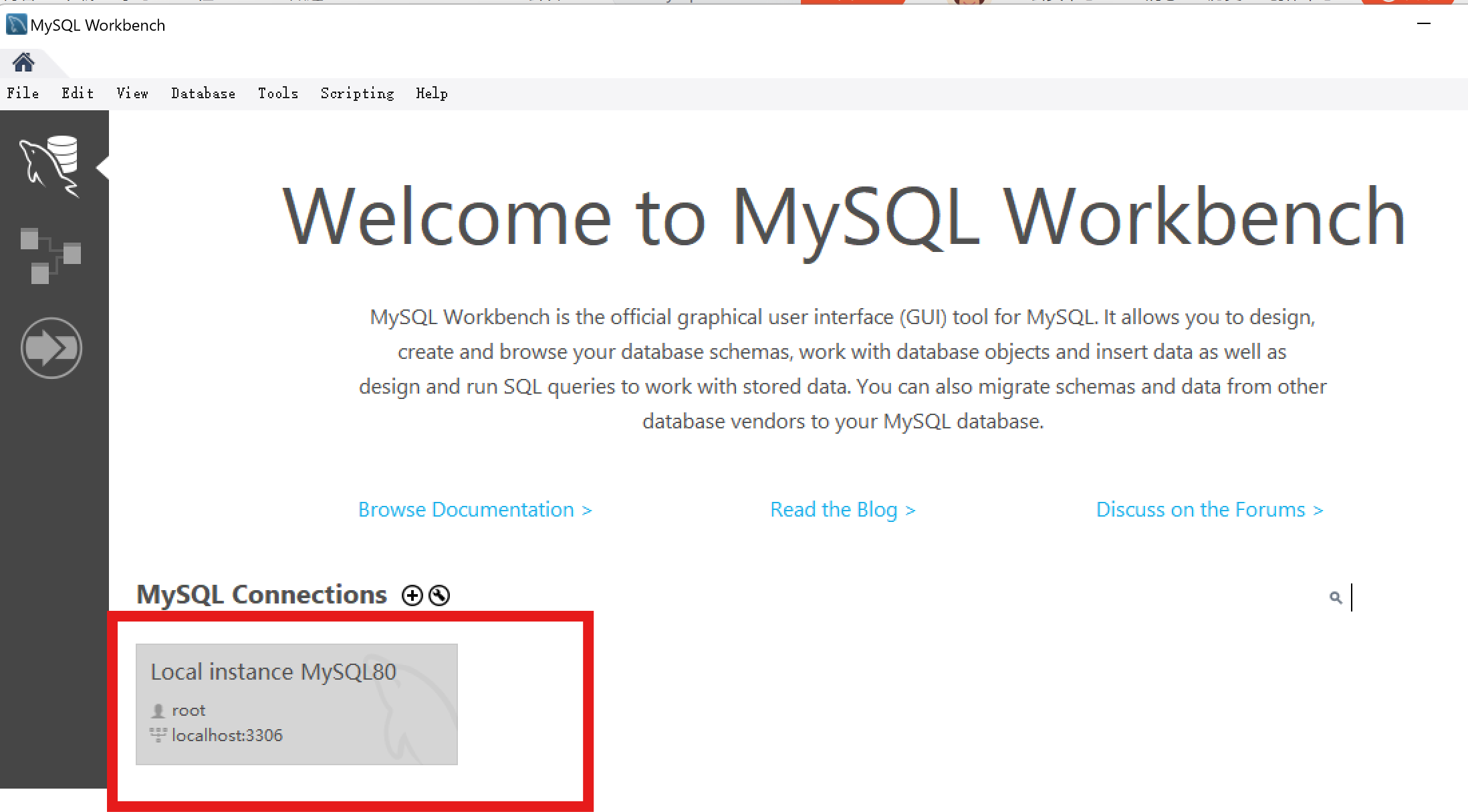
输入root账号的密码(安装时设置的密码),单击【OK】按钮。

显示如下,成功进入MySQL。
提醒:如果之前通过命令提示符访问MySQL,改为使用workbench时,请退出MySQL在命令提示符中的登录。