文心一言 VS 讯飞星火 VS chatgpt （291）-- 算法导论21.3 4题

news2024/12/23 1:56:13

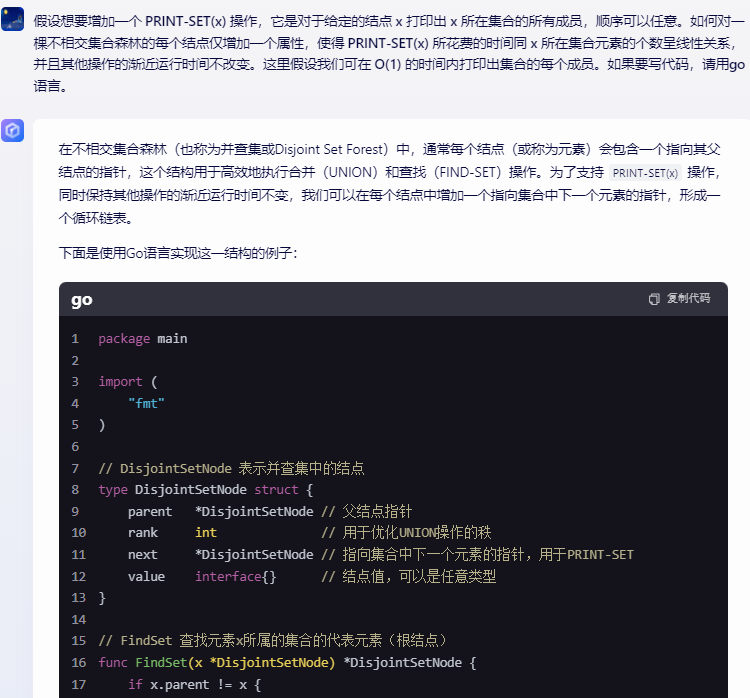
四、假设想要增加一个 PRINT-SET(x) 操作，它是对于给定的结点 x 打印出 x 所在集合的所有成员，顺序可以任意。如何对一棵不相交集合森林的每个结点仅增加一个属性，使得 PRINT-SET(x) 所花费的时间同 x 所在集合元素的个数呈线性关系，并且其他操作的渐近运行时间不改变。这里假设我们可在 O(1) 的时间内打印出集合的每个成员。如果要写代码，请用go语言。

文心一言：

在不相交集合森林（也称为并查集或Disjoint Set Forest）中，通常每个结点（或称为元素）会包含一个指向其父结点的指针，这个结构用于高效地执行合并（UNION）和查找（FIND-SET）操作。为了支持 PRINT-SET(x) 操作，同时保持其他操作的渐近运行时间不变，我们可以在每个结点中增加一个指向集合中下一个元素的指针，形成一个循环链表。

下面是使用Go语言实现这一结构的例子：

package main

import (
	"fmt"
)

// DisjointSetNode 表示并查集中的结点
type DisjointSetNode struct {
	parent   *DisjointSetNode // 父结点指针
	rank     int              // 用于优化UNION操作的秩
	next     *DisjointSetNode // 指向集合中下一个元素的指针，用于PRINT-SET
	value    interface{}      // 结点值，可以是任意类型
}

// FindSet 查找元素x所属的集合的代表元素（根结点）
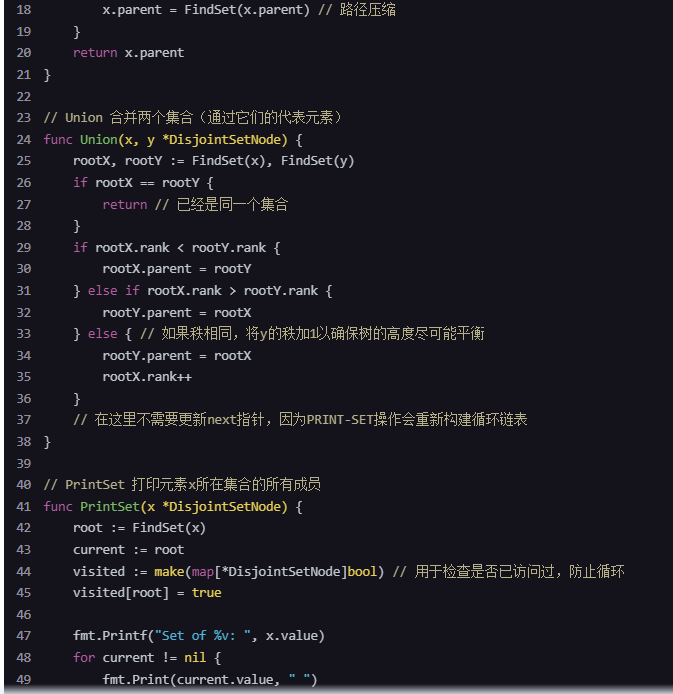
func FindSet(x *DisjointSetNode) *DisjointSetNode {
	if x.parent != x {
		x.parent = FindSet(x.parent) // 路径压缩
	}
	return x.parent
}

// Union 合并两个集合（通过它们的代表元素）
func Union(x, y *DisjointSetNode) {
	rootX, rootY := FindSet(x), FindSet(y)
	if rootX == rootY {
		return // 已经是同一个集合
	}
	if rootX.rank < rootY.rank {
		rootX.parent = rootY
	} else if rootX.rank > rootY.rank {
		rootY.parent = rootX
	} else { // 如果秩相同，将y的秩加1以确保树的高度尽可能平衡
		rootY.parent = rootX
		rootX.rank++
	}
	// 在这里不需要更新next指针，因为PRINT-SET操作会重新构建循环链表
}

// PrintSet 打印元素x所在集合的所有成员
func PrintSet(x *DisjointSetNode) {
	root := FindSet(x)
	current := root
	visited := make(map[*DisjointSetNode]bool) // 用于检查是否已访问过，防止循环
	visited[root] = true

	fmt.Printf("Set of %v: ", x.value)
	for current != nil {
		fmt.Print(current.value, " ")
		next := current.next
		// 如果遇到nil或已访问过的结点，说明循环结束
		for next != nil && visited[next] {
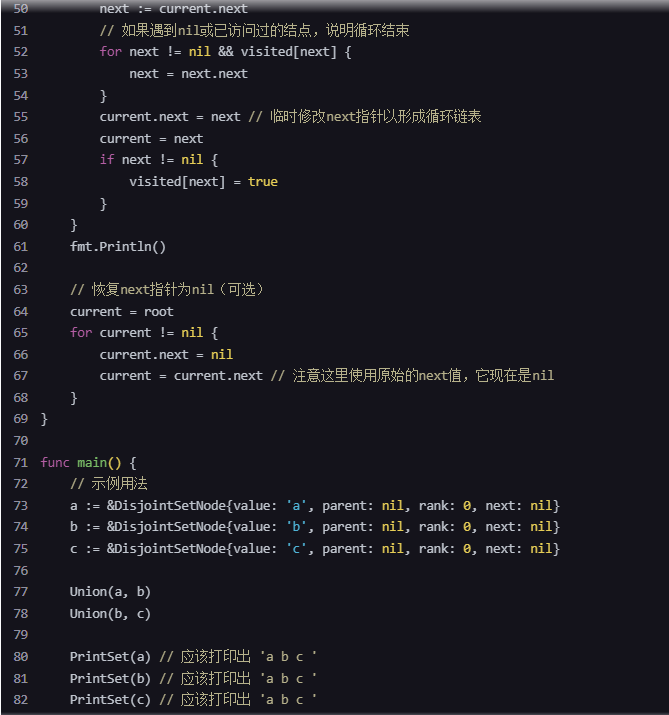
			next = next.next
		}
		current.next = next // 临时修改next指针以形成循环链表
		current = next
		if next != nil {
			visited[next] = true
		}
	}
	fmt.Println()

	// 恢复next指针为nil（可选）
	current = root
	for current != nil {
		current.next = nil
		current = current.next // 注意这里使用原始的next值，它现在是nil
	}
}

func main() {
	// 示例用法
	a := &DisjointSetNode{value: 'a', parent: nil, rank: 0, next: nil}
	b := &DisjointSetNode{value: 'b', parent: nil, rank: 0, next: nil}
	c := &DisjointSetNode{value: 'c', parent: nil, rank: 0, next: nil}

	Union(a, b)
	Union(b, c)

	PrintSet(a) // 应该打印出 'a b c '
	PrintSet(b) // 应该打印出 'a b c '
	PrintSet(c) // 应该打印出 'a b c '
}

注意，在上面的 PrintSet 函数中，我们使用了 visited 映射来避免在循环链表中重复访问元素。因为 next 指针在集合合并时不会被更新，所以我们在打印集合时需要手动构建循环链表。打印完集合后，我们将 next 指针恢复为 nil（这是可选的，取决于你是否想在打印后保持集合的内部状态不变）。

此外，上述代码中的 FindSet 使用了路径压缩技术来优化查找操作，使得 FindSet 的平均时间复杂度接近于常数。而 Union 操作则通过比较秩来

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

讯飞星火：

为了实现 PRINT-SET(x) 操作，我们可以在每个结点上添加一个指向其父节点的指针。这样，当我们想要打印一个集合的所有成员时，我们可以通过遍历这个集合的所有结点并打印它们来实现。具体来说，我们可以从给定的结点 x 开始，沿着父节点指针向上遍历，直到找到一个没有父节点的结点（即根节点）。然后，我们可以再次遍历从根节点到 x 的所有路径，打印出所有遇到的结点。

以下是使用 Go 语言实现的代码：

package main

import "fmt"

type Node struct {
    parent *Node
    value  int
}

func NewNode(value int) *Node {
    return &Node{parent: nil, value: value}
}

func (n *Node) SetParent(p *Node) {
    n.parent = p
}

func PrintSet(x *Node) {
    if x == nil {
        return
    }

    // 找到根节点
    for x.parent != nil {
        x = x.parent
    }

    // 打印从根节点到当前结点的所有路径上的结点
    for y := x; y != nil; y = y.parent {
        fmt.Println(y.value)
    }
}

func main() {
    // 创建一个简单的不相交集合森林示例
    node1 := NewNode(1)
    node2 := NewNode(2)
    node3 := NewNode(3)
    node4 := NewNode(4)

    node2.SetParent(node1)
    node3.SetParent(node1)
    node4.SetParent(node2)

    // 测试 PRINT-SET 操作
    PrintSet(node4) // 输出：1, 2, 4
}

在这个实现中，我们为每个结点添加了一个指向其父节点的指针。PrintSet 函数首先找到给定结点的根节点，然后遍历从根节点到给定结点的所有路径，打印出所有遇到的结点。这样，PRINT-SET(x) 的时间复杂度就是 O(log n)，其中 n 是树的高度。其他操作的时间复杂度保持不变。

360智脑：

为了实现 PRINT-SET(x) 操作，我们可以为每个结点添加一个额外的属性，即指向其所在集合的代表结点的指针。这样，当我们需要打印一个集合时，我们可以通过遍历从给定结点到代表结点的路径上的所有结点来实现。由于路径上的结点数量等于集合中的元素数量，因此这个操作的时间复杂度与集合的大小成线性关系。

以下是一个使用 Go 语言实现的示例代码：

type Node struct {
    parent *Node // 父节点指针
    rank   int   // 用于路径压缩和按秩合并的秩
    setRep *Node // 指向集合代表的指针
}

// 初始化结点
func MakeSet(x *Node) {
    x.parent = x
    x.rank = 0
    x.setRep = x // 初始时，每个结点都是自己集合的代表
}

// 查找结点的代表结点，并进行路径压缩
func FindSet(x *Node) *Node {
    if x != x.parent {
        x.parent = FindSet(x.parent)
    }
    return x.parent
}

// 合并两个集合
func Union(x *Node, y *Node) {
    link(FindSet(x), FindSet(y))
}

// 链接两个结点，按秩合并
func link(x *Node, y *Node) {
    if x.rank > y.rank {
        y.parent = x
        y.setRep = x // 更新 y 的集合代表指针
    } else {
        x.parent = y
        x.setRep = y // 更新 x 的集合代表指针
        if x.rank == y.rank {
            y.rank++
        }
    }
}

// 打印集合
func PrintSet(x *Node) {
    rep := FindSet(x)
    printSetRecursive(rep)
}

// 递归打印集合
func printSetRecursive(node *Node) {
    fmt.Println(node)
    current := node
    for current.parent != current {
        current = current.parent
        fmt.Println(current)
    }
}

// 测试代码
func main() {
    nodes := []*Node{&Node{}, &Node{}, &Node{}, &Node{}}
    for _, node := range nodes {
        MakeSet(node)
    }
    Union(nodes[0], nodes[1])
    Union(nodes[2], nodes[3])
    Union(nodes[1], nodes[2])
    PrintSet(nodes[0])
}

在这个实现中，MakeSet、FindSet 和 Union 函数保持了原有的时间复杂度不变，而 PrintSet 函数通过递归地打印从给定结点到代表结点的路径上的所有结点来实现打印集合的操作。由于每次递归都会打印一个结点，因此打印整个集合的时间复杂度与集合的大小成线性关系。

智谱清言：

为了实现 PRINT-SET(x) 操作，我们可以为每个结点添加一个额外的属性，即指向其所在集合的代表结点的指针。这样，当我们需要打印一个集合时，我们可以通过遍历从给定结点到代表结点的路径上的所有结点来实现。由于路径上的结点数量等于集合中的元素数量，因此这个操作的时间复杂度与集合的大小成线性关系。

以下是一个使用 Go 语言实现的示例代码：

type Node struct {
    parent *Node // 父节点指针
    rank   int   // 用于路径压缩和按秩合并的秩
    setRep *Node // 指向集合代表的指针
}

// 初始化结点
func MakeSet(x *Node) {
    x.parent = x
    x.rank = 0
    x.setRep = x // 初始时，每个结点都是自己集合的代表
}

// 查找结点的代表结点，并进行路径压缩
func FindSet(x *Node) *Node {
    if x != x.parent {
        x.parent = FindSet(x.parent)
    }
    return x.parent
}

// 合并两个集合
func Union(x *Node, y *Node) {
    link(FindSet(x), FindSet(y))
}

// 链接两个结点，按秩合并
func link(x *Node, y *Node) {
    if x.rank > y.rank {
        y.parent = x
        y.setRep = x // 更新 y 的集合代表指针
    } else {
        x.parent = y
        x.setRep = y // 更新 x 的集合代表指针
        if x.rank == y.rank {
            y.rank++
        }
    }
}

// 打印集合
func PrintSet(x *Node) {
    rep := FindSet(x)
    printSetRecursive(rep)
}

// 递归打印集合
func printSetRecursive(node *Node) {
    fmt.Println(node)
    current := node
    for current.parent != current {
        current = current.parent
        fmt.Println(current)
    }
}

// 测试代码
func main() {
    nodes := []*Node{&Node{}, &Node{}, &Node{}, &Node{}}
    for _, node := range nodes {
        MakeSet(node)
    }
    Union(nodes[0], nodes[1])
    Union(nodes[2], nodes[3])
    Union(nodes[1], nodes[2])
    PrintSet(nodes[0])
}

在这个实现中，MakeSet、FindSet 和 Union 函数保持了原有的时间复杂度不变，而 PrintSet 函数通过递归地打印从给定结点到代表结点的路径上的所有结点来实现打印集合的操作。由于每次递归都会打印一个结点，因此打印整个集合的时间复杂度与集合的大小成线性关系。

天工：

为了实现 PRINT-SET(x) 操作，我们需要在不相交集合森林中的每个结点上增加一个指向其父节点的指针。这样，我们可以通过沿着树的路径从结点 x 向上遍历到根节点，然后从根节点向下遍历到所有叶子节点来打印出集合的所有成员。这种遍历可以在每个结点上花费常数时间，因此总时间是线性的。

下面是一个使用Go语言实现的示例代码：

type DisjointSetNode struct {
    parent *DisjointSetNode // 指向父节点的指针
    rank   int              // 用于路径压缩和按秩合并的秩
    value  string           // 结点的值
}

func MakeSet(x *DisjointSetNode) {
    x.parent = x
    x.rank = 0
}

func FindSet(x *DisjointSetNode) *DisjointSetNode {
    if x.parent != x {
        x.parent = FindSet(x.parent) // 路径压缩
    }
    return x.parent
}

func Union(x *DisjointSetNode, y *DisjointSetNode) {
    link(FindSet(x), FindSet(y))
}

func link(x *DisjointSetNode, y *DisjointSetNode) {
    if x.rank > y.rank {
        y.parent = x
    } else {
        x.parent = y
        if x.rank == y.rank {
            y.rank++
        }
    }
}

func PrintSet(x *DisjointSetNode) {
    root := FindSet(x)
    printHelper(root)
}

func printHelper(node *DisjointSetNode) {
    if node != nil {
        fmt.Println(node.value)
        printHelper(node.parent)
    }
}

// 示例用法
func main() {
    nodes := []*DisjointSetNode{
        &DisjointSetNode{value: "A"},
        &DisjointSetNode{value: "B"},
        &DisjointSetNode{value: "C"},
        &DisjointSetNode{value: "D"},
    }
    for _, node := range nodes {
        MakeSet(node)
    }
    Union(nodes[0], nodes[1])
    Union(nodes[2], nodes[3])
    Union(nodes[0], nodes[2])
    PrintSet(nodes[1]) // 打印出集合 {"A", "B", "C", "D"}
}

在这个实现中，MakeSet 函数创建一个新的集合，其中包含单个元素。FindSet 函数找到一个元素的集合的代表，并在返回之前执行路径压缩。Union 函数将两个集合合并为一个。PrintSet 函数打印出给定结点所在集合的所有成员。

请注意，这个实现假设我们可以在常数时间内打印出集合的每个成员。如果打印操作不是常数时间，那么 PrintSet 的总时间将与集合的大小成正比。此外，这个实现没有改变其他操作（如 MakeSet、FindSet 和 Union）的渐近运行时间。

灵小智：

为了实现 PRINT-SET(x) 操作，我们可以通过修改不相交集合森林的每个结点，使其具有指向集合中所有成员的指针。这样，当调用 PRINT-SET(x) 时，只需遍历该结点指向的所有成员并打印出来，时间复杂度与集合元素个数成线性关系。

以下是一个示例的 Go 代码，演示如何修改不相交集合森林的结点以支持 PRINT-SET(x) 操作：

package main

import "fmt"

type Node struct {
	parent *Node
	rank   int
	members []int
}

func MakeSet(x int) *Node {
	return &Node{parent: nil, rank: 0, members: []int{x}}
}

func Find(node *Node) *Node {
	if node.parent == nil {
		return node
	}
	return Find(node.parent)
}

func Union(x, y *Node) {
	rootX := Find(x)
	rootY := Find(y)

	if rootX == rootY {
		return
	}

	if rootX.rank < rootY.rank {
		rootX, rootY = rootY, rootX
	}

	rootY.parent = rootX

	rootX.members = append(rootX.members, rootY.members...)

	if rootY.rank == rootX.rank {
		rootX.rank++
	}
}

func PrintSet(x *Node) {
	for _, member := range x.members {
		fmt.Println(member)
	}
}

func main() {
	// 示例用法
	node1 := MakeSet(1)
	node2 := MakeSet(2)
	Union(node1, node2)

	PrintSet(node1)
}

通过将每个结点扩展为包含成员列表，我们可以在 O(1) 的时间内打印出集合的每个成员，同时保持其他操作的渐近运行时间不变。

chatgpt：

为了实现给每个节点增加一个属性以支持 PRINT-SET(x) 操作的线性时间复杂度，可以使用路径压缩和按秩合并的思想。具体代码如下（Go语言）：

package main

import "fmt"

type Node struct {
	parent *Node
	rank   int
	value  interface{} // 节点的值，可以根据需求修改类型
}

func MakeSet(x *Node) {
	x.parent = x
	x.rank = 0
}

func Find(x *Node) *Node {
	if x != x.parent {
		x.parent = Find(x.parent) // 路径压缩
	}
	return x.parent
}

func Union(x, y *Node) {
	rootX := Find(x)
	rootY := Find(y)

	if rootX == rootY {
		return
	}

	if rootX.rank < rootY.rank {
		rootX.parent = rootY
	} else if rootX.rank > rootY.rank {
		rootY.parent = rootX
	} else {
		rootY.parent = rootX
		rootX.rank++
	}
}

// 增加一个属性用于记录集合元素数量，并在合并时更新该属性值
func AddPrintSetAttribute(root *Node, value interface{}) {
	root.value = value // 设置节点值为集合元素数量
}

// 打印出给定节点所在集合的所有成员（遍历打印）
func PrintSet(root *Node) {
	current := Find(root)

	for current != nil {
		fmt.Println(current.value)
		current = current.parent
	}
}

func main() {
	node1 := &Node{}
	node2 := &Node{}
	node3 := &Node{}
	node4 := &Node{}

	MakeSet(node1)
	MakeSet(node2)
	MakeSet(node3)
	MakeSet(node4)

	AddPrintSetAttribute(node1, 1)
	AddPrintSetAttribute(node2, 2)
	AddPrintSetAttribute(node3, 3)
	AddPrintSetAttribute(node4, 4)

	Union(node1, node2) // 合并集合 {1, 2}
	Union(node3, node4) // 合并集合 {3, 4}

	PrintSet(Find(node1)) // 打印出集合 {1, 2} 的所有成员
	PrintSet(Find(node3)) // 打印出集合 {3, 4} 的所有成员
}

上述代码使用不相交集合森林的数据结构，并在每个节点中增加一个属性来记录集合元素数量。通过路径压缩和按秩合并的策略，使得 PRINT-SET(x) 操作的时间复杂度与 x 所在集合元素个数成线性关系，并且其他操作（如 MakeSet、Find、Union）的渐近运行时间不变。最后，在打印时遍历打印出给定节点所在集合的所有成员。

混元：

为了实现 PRINT-SET(x) 操作，我们可以在每个结点 x 上增加一个属性 parent，用来记录 x 的父结点。同时，我们需要一个字典（或哈希表）来存储每个集合的根结点及其成员列表。这样，在执行 PRINT-SET(x) 时，我们可以从 x 开始向上查找其根结点，然后打印出该集合的所有成员。

首先，我们需要定义一个结构体来表示结点，并包含 parent 属性：

type Node struct {
    value int
    parent *Node
}

接下来，我们需要实现以下几个操作：

  1. 初始化不相交集合森林
  2. 查找结点的根结点
  3. 合并两个集合
  4. 执行 PRINT-SET(x) 操作

以下是相应的 Go 语言实现：

package main

import "fmt"

type Node struct {
	value int
	parent *Node
}

// 初始化不相交集合森林
func initDisjointSetForest(size int) []*Node {
	nodes := make([]*Node, size)
	for i := range nodes {
		nodes[i] = &Node{value: i}
	}
	return nodes
}

// 查找结点的根结点
func find(node *Node) *Node {
	if node.parent == nil {
		return node
	}
	node.parent = find(node.parent) // 路径压缩
	return node.parent
}

// 合并两个集合
func union(node1, node2 *Node) {
	root1 := find(node1)
	root2 := find(node2)
	if root1 != root2 {
		root1.parent = root2
	}
}

// 执行 PRINT-SET(x) 操作
func printSet(node *Node, sets map[int][]*Node) {
	root := find(node)
	for _, n := range sets[root.value] {
		fmt.Printf("%d ", n.value)
	}
	fmt.Println()
}

func main() {
	nodes := initDisjointSetForest(10)
	sets := make(map[int][]*Node)

	for _, node := range nodes {
		sets[node.value] = append(sets[node.value], node)
	}

	union(nodes[1], nodes[2])
	union(nodes[3], nodes[4])
	union(nodes[5], nodes[6])

	printSet(nodes[1], sets) // 输出: 1 2
	printSet(nodes[3], sets) // 输出: 3 4
	printSet(nodes[5], sets) // 输出: 5 6
}

在这个实现中，PRINT-SET(x) 操作的时间复杂度为 O(n)，其中 n 是 x 所在集合的元素个数。其他操作的渐近运行时间保持不变。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1873075.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

新手必备！短视频剪辑常用的18个技巧——剪映篇

新手必备！短视频剪辑常用的18个技巧——剪映篇

导入素材&#xff1a;这里我们可以选择自己拍摄好的素材&#xff08;图片、视频或录制好的音频&#xff09;&#xff0c;按照顺序导入剪辑区剪辑。这一步是剪辑的基础&#xff0c;确定剪辑的大体思路与成片框架&#xff01;别忽略了&#xff0c;剪映官方素材库提供的素材&#…
阅读更多...
Mysql序列

Mysql序列

&#x1f49d;&#x1f49d;&#x1f49d;首先&#xff0c;欢迎各位来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里不仅可以有所收获&#xff0c;同时也能感受到一份轻松欢乐的氛围&#xff0c;祝你生活愉快&#xff01; &#x1f49d;&#x1f49…
阅读更多...
SSL证书不安全问题处理方案

SSL证书不安全问题处理方案

正常使用情况&#xff1a; verifyFalse&#xff1a;代表不使用SSL证书校验、 以上方式在coze中使用失败 response requests.get(url, verifyFalse).text替换方案&#xff1a;使用httpx import httpx with httpx.Client(verifyFalse) as client:response client.get(url)参考…
阅读更多...
气膜移动宴会厅：现代化宴会解决方案—轻空间

气膜移动宴会厅：现代化宴会解决方案—轻空间

随着社会经济的发展和人们生活水平的提高&#xff0c;各类宴会、庆典和活动的需求日益增加。然而&#xff0c;传统的宴会厅受限于固定的地点和昂贵的建设成本&#xff0c;无法灵活应对不同规模和地点的需求。在此背景下&#xff0c;气膜移动宴会厅作为一种创新的解决方案&#…
阅读更多...
定制课程引领，师资培训助力——树莓集团政企合作育人新篇章

定制课程引领，师资培训助力——树莓集团政企合作育人新篇章

树莓集团通过定制课程和师资培训两种方式&#xff0c;为高校提供了更加全面、系统、专业的教育资源。这些资源不仅提高了学生的专业素养和实践能力&#xff0c;也促进了教师的专业发展。 一、定制课程 1、行业需求导向&#xff1a;树莓集团根据数字产业及相关行业的发展趋势和…
阅读更多...
Ubuntu系统中创建桌面快捷方式和添加Favorites

Ubuntu系统中创建桌面快捷方式和添加Favorites

一. Ubuntu系统中创建软件的桌面快捷方式 Ubuntu桌面创建某个软件的桌面快捷方式&#xff0c;一个直观的方法。 方法1. 在图像界面下&#xff0c;一层一层地打开文件目录软件快捷方式/usr/share/applications/ 方法2. 或者在终端运行$ nautilus /usr/share/applications/ …
阅读更多...
点心甜品商城小程序店铺是怎样开展的

点心甜品商城小程序店铺是怎样开展的

很多人非常喜欢甜品点心&#xff0c;包括在宴会、送礼、家庭聚会等场景也有应用度&#xff0c;该赛道也存在头部品牌&#xff0c;其余则是以地区为主的线下店&#xff0c;线上则主要以外卖及电商快递等方式经营。 除了线下店和其它平台进驻外&#xff0c;商家还需要多渠道获客…
阅读更多...
华为仓颉编程语言：未来的期待与挑战

华为仓颉编程语言：未来的期待与挑战

在刚刚过去的华为开发者大会&#xff08;HDC&#xff09;上&#xff0c;除了发布鸿蒙新一代操作系统外&#xff0c;备受期待的仓颉编程语言也正式亮相。对于这一新语言的发布&#xff0c;业界和程序员社区给予了高度关注。本文将深入探讨仓颉编程语言的特点、应用前景及其面临的…
阅读更多...
Linux系统上部署Whisper。

Linux系统上部署Whisper。

Whisper是一个开源的自动语音识别&#xff08;ASR&#xff09;模型&#xff0c;最初由OpenAI发布。要在本地Linux系统上部署Whisper&#xff0c;你可以按照以下步骤进行&#xff1a; 1. 创建虚拟环境 为了避免依赖冲突&#xff0c;建议在虚拟环境中进行部署。创建并激活一个新…
阅读更多...
16位诺奖经济学奖得主联名信：特朗普就是“通胀炸弹”

16位诺奖经济学奖得主联名信：特朗普就是“通胀炸弹”

经济学家警告特朗普“不负责任的财政预算将重燃通胀”&#xff0c;尤其是其对外国商品征收普遍关税和驱逐移民的政策&#xff0c;可能会对美国乃至全球经济产生灾难性长期影响。但华尔街分析师称&#xff0c;两党如今都是贸易保护主义者&#xff0c;通胀注定会回升&#xff0c;…
阅读更多...
STM32 HAL库 外部中断 实现按键控制LED亮灭

STM32 HAL库 外部中断 实现按键控制LED亮灭

目录 1、为什么使用GPIO外部中断控制LED亮灭&#xff1f; 2、NVIC嵌套向量中断控制器 3、EXTI外部中断 4、项目的硬件排线 5、STM32CUBE_MX配置 6、HAL库代码 7、实际效果 1、为什么使用GPIO外部中断控制LED亮灭&#xff1f; 实现LED亮灭控制有很多方式&#xff0c;其中…
阅读更多...
【机器学习】在【PyCharm中的学习】：从【基础到进阶的全面指南】

【机器学习】在【PyCharm中的学习】：从【基础到进阶的全面指南】

目录 第一步&#xff1a;基础准备 1.1 Python基础 1.1.1 学习Python的基本语法 变量和数据类型&#xff1a; 1.1.2 控制流 条件语句&#xff1a; 循环语句&#xff1a; 1.1.3 函数和模块 函数&#xff1a; 模块&#xff1a; 1.2 安装PyCharm 1.2.1 下载并安装 第二…
阅读更多...
听说网络安全行业是IT行业最后的红利？

听说网络安全行业是IT行业最后的红利？

前言 2023年网络安全行业的前景看起来非常乐观。根据当前的趋势和发展&#xff0c;一些趋势和发展可能对2023年网络安全行业产生影响&#xff1a; 5G技术的广泛应用&#xff1a;5G技术的普及将会使互联网的速度更快&#xff0c;同时也将带来更多的网络威胁和安全挑战。网络安全…
阅读更多...
tr、cut、split、grep -E

tr、cut、split、grep -E

目录 tr命令&#xff1a;替换和删除 cut命令&#xff1a;快速裁剪 split命令&#xff1a;文件拆分 文件合并 面试题 1.现在有一个日志文件&#xff0c;有5个G&#xff0c;能不能快速的打开 2.cat合并和paste合并之间的区别&#xff1f; 3.统计当前主机的连接状态&#…
阅读更多...
初学51单片机之长短键应用定时炸弹及扩展应用

初学51单片机之长短键应用定时炸弹及扩展应用

51单片机RAM区域划分 51单片机的RAM分为两个部分&#xff0c;一块是片内RAM&#xff0c;一块是片外RAM。 data&#xff1a; 片内RAM从 0x00 ~0x7F 寻址范围&#xff08;0-127&#xff09; 容量共128B idata: 片外RAM从 0x00~0xFF 寻址范围(0-255) 容量共256B pdata&am…
阅读更多...
总结一下Linux、Windows、Ubuntu、Debian、CentOS等到底是啥？及它们的区别是什么

总结一下Linux、Windows、Ubuntu、Debian、CentOS等到底是啥？及它们的区别是什么

小朋友你总是有很多问好 你是否跟我一样&#xff0c;不是计算机科班出身&#xff0c;很多东西都是拿着在用&#xff0c;并不知道为什么&#xff0c;或者对于它们的概念也是稀里糊涂的&#xff0c;比如今天说的这个。先简单描述下&#xff0c;我先前的疑问&#xff1a; Linux是…
阅读更多...
爬取电商商品详情数据的经验分享（数据已封装API可调用）

爬取电商商品详情数据的经验分享（数据已封装API可调用）

一、引言 随着电子商务的蓬勃发展&#xff0c;商品详情数据成为了商家、数据分析师和研究者们关注的焦点。这些数据不仅可以帮助商家了解市场趋势、优化产品策略&#xff0c;还能为研究者提供丰富的数据源&#xff0c;以支持各种学术研究。然而&#xff0c;获取这些数据的难度…
阅读更多...
鸿蒙开发设备管理：【@ohos.brightness (屏幕亮度)】

鸿蒙开发设备管理：【@ohos.brightness (屏幕亮度)】

屏幕亮度 该模块提供屏幕亮度的设置接口。 说明&#xff1a; 本模块首批接口从API version 7开始支持。后续版本的新增接口&#xff0c;采用上角标单独标记接口的起始版本。 导入模块 import brightness from ohos.brightness;brightness.setValue setValue(value: number):…
阅读更多...
如何快捷批量处理图片？图片批量改大小、格式、尺寸的方法

如何快捷批量处理图片？图片批量改大小、格式、尺寸的方法

怎么把图片批量修改成同一尺寸呢&#xff1f;图片在日常工作和生活中有很多的用途&#xff0c;每天都会需要使用不同类型的图片来获取我们需要的内容。在使用图片的时候&#xff0c;经常会遇到比较常见的几个限制问题&#xff0c;比如图片大小、图片尺寸、图片格式等&#xff0…
阅读更多...
【深度学习】图形模型基础(1):使用潜在变量模型进行数据分析的box循环

【深度学习】图形模型基础(1):使用潜在变量模型进行数据分析的box循环

1.绪论 探索数据背后的隐藏规律&#xff0c;这不仅是数据分析的艺术&#xff0c;更是概率模型展现其威力的舞台。在这一过程中&#xff0c;潜在变量模型尤为关键&#xff0c;它成为了数据驱动问题解决的核心引擎。潜在变量模型的基本理念在于&#xff0c;那些看似复杂、杂乱无…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023