第一节. 定积分

一. 定积分的概念

1. 定义

1. 分割，无限分份
2. 求和：取任意一点
3. 取极限：极限存在则可积

1. 定积分表示一个数值，只与积分区间与被积函数有关，
2. 利用定积分定义求极限
   

 

2. 定积分存在定理

 

3. 定积分的几何意义与求解

 

二. 定积分的性质

1. 不等式

 

2. 中值定理

 

三. 积分上限（为x）函数

1. 积分上限函数定义

1. fx在区间[a,b]的原函数
2. 连续函数必有原函数

 

2. 积分函数求导

 

3. 积分函数的奇偶性变化

 

四. 定积分的计算

公式	说明
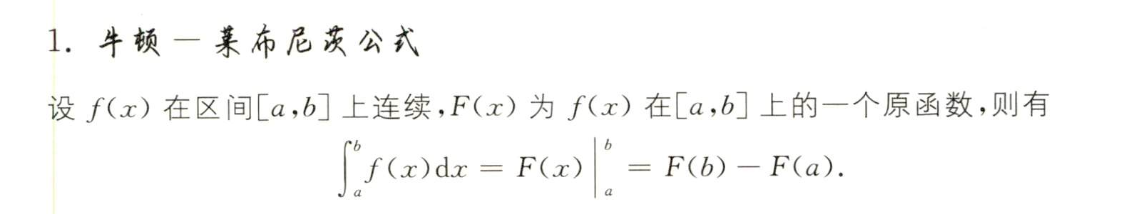	直接找原函数
	x换元，积分上下限，以及dx都换元
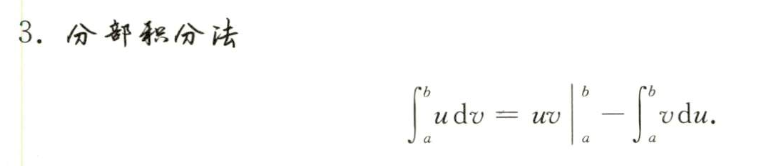	根据上节的方法
	利用奇偶性、周期性
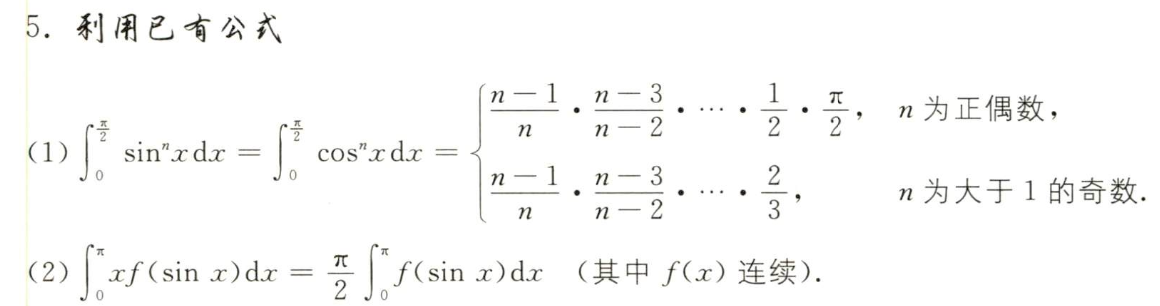	sinx、cosx的积分

 

第二节. 反常积分

一. 无穷区间上的积分：反常积分

1. 定义

1. 反常积分：积分区间是无穷的。
2. 反常积分的收敛或发散。

 

2. 性质一：比较判别

1. 小的发散则大的一定发散
2. 大的收敛则小的一定收敛

 

3. 性质二：极限形式

1. 常数说明同敛散性
2. =0，说明分母比分子敛散性差，但如果分母收敛则分子一定收敛
3. 无穷则相反，敛散性都差，看敛散性好的，分母发散则分子一定发散。

 

二. 无界函数的反常积分

1. 反常积分之开区间：瑕积分

1. 瑕点：开区间的边界
2. 瑕积分的敛散性：积分+极限

 

2. 性质：比较判别法

与无穷区间是类似的

 
常用结论

 

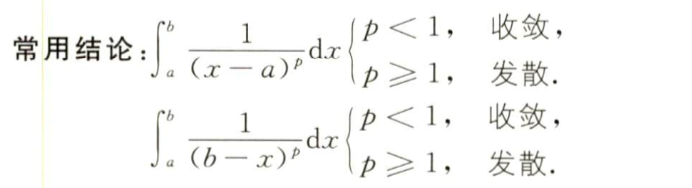
第三节：几何应用

1. 平面图形的面积：

1. 函数减函数
2. 极坐标：角度

 

2. 旋转体体积

1. 找到积分元素：都是面积
2. 找到积分上下限。

 

3. 曲线弧长

1. 常见函数
2. 参数函数
3. 极坐标函数

 

4. 旋转体侧面积

ing。