傅里叶变换

对傅里叶变换了解不是很清楚的朋友推荐一下这个帖子，讲得很详细 傅里叶变换

源码

先看源码链接

#include "opencv2/core.hpp"
#include "opencv2/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"
 
#include <iostream>
 
using namespace cv;
using namespace std;
 
static void help(char ** argv)
{
    cout << endl
         << "This program demonstrated the use of the discrete Fourier transform (DFT). " << endl
         << "The dft of an image is taken and it's power spectrum is displayed." << endl << endl
         << "Usage:" << endl
         << argv[0] << " [image_name -- default lena.jpg]" << endl << endl;
}
 
int main(int argc, char ** argv)
{
    help(argv);

    const char* filename = argc >=2 ? argv[1] : "lena.jpg";

    // 读取灰度图像
    Mat I = imread(samples::findFile(filename), IMREAD_GRAYSCALE);
    if(I.empty()){
        cout << "Error opening image" << endl;
        return EXIT_FAILURE;
    }

    // 扩展输入图像到最优尺寸
    Mat padded; 
    int m = getOptimalDFTSize(I.rows);
    int n = getOptimalDFTSize(I.cols); 
    copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0));

    // 创建包含实部和虚部的平面
    Mat planes[] = {Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F)};
    Mat complexI;
    merge(planes, 2, complexI); // 合并成一个复数矩阵

    // 进行DFT变换
    dft(complexI, complexI);

    // 计算幅度谱并转换为对数尺度
    split(complexI, planes); // 分离实部和虚部
    magnitude(planes[0], planes[1], planes[0]); // 计算幅度
    Mat magI = planes[0];

    magI += Scalar::all(1); // 转换为对数尺度
    log(magI, magI);

    // 如果频谱的行列是奇数，则进行裁剪
    magI = magI(Rect(0, 0, magI.cols & -2, magI.rows & -2));

    // 重新排列傅里叶图像的象限，使原点在图像中心
    int cx = magI.cols/2;
    int cy = magI.rows/2;

    Mat q0(magI, Rect(0, 0, cx, cy)); // 左上
    Mat q1(magI, Rect(cx, 0, cx, cy)); // 右上
    Mat q2(magI, Rect(0, cy, cx, cy)); // 左下
    Mat q3(magI, Rect(cx, cy, cx, cy)); // 右下

    Mat tmp;
    q0.copyTo(tmp);
    q3.copyTo(q0);
    tmp.copyTo(q3);

    q1.copyTo(tmp);
    q2.copyTo(q1);
    tmp.copyTo(q2);

    // 归一化幅度图像到0-1之间
    normalize(magI, magI, 0, 1, NORM_MINMAX);

    // 显示原图像和频谱图像
    imshow("Input Image", I);
    imshow("spectrum magnitude", magI);
    waitKey();

    return EXIT_SUCCESS;
}
}

原理

傅里叶变换将图像分解为其正弦和余弦分量。这就意味着，傅里叶变换可以将复杂的图像表示为不同频率和振幅的正弦波和余弦波的组合，这些波的频率和相位描述了图像的周期性结构。低频成分对应图像中的大面积平滑区域，高频成分对应图像中的边缘和细节。

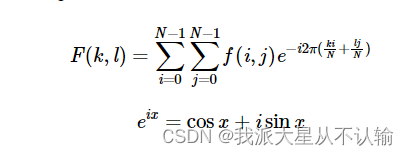
空间域和频域

• f : 图像在空间域中的值，即图像像素的强度值。
• F ：图像在频域中的值，即通过傅里叶变换后的结果。

傅里叶变换结果

傅里叶变换将图像从空间域转换到频域，其结果是复数，这意味着每个频率分量有两个部分：实部和虚部。通过所保留地完整的复数信息，可以重新变回空间域。链接

显示频域图像

有两种方式来显示频域图像：

1. 实部和虚部图像：分别显示傅里叶变换结果的实部和虚部
2. 幅度和相位图像： 幅度图像和相位图像分别显示每个频率分量的强度和相位信息。

在图像处理中，通常情况下我们只会针对幅度图像做进一步研究，因为其包含了图像几何结构的所有信息。幅度图像显示了频率分量的强度，这与图像的结构和边缘有关。

对于数字图像来说，其经过傅里叶变换所获得的幅度图像是离散的，这也就意味着他们可以从指定的域值中取值，比如说，在基本的灰度图中，像素值通常在0到255之间，因此傅里叶变换也需要是离散类型的。

以下是一个以灰度图为输入例子的步骤详解。

Steps

1. 将图像拓展到合适的大小
   DFT的性能主要取决于图像的大小，其会在当图像大小为2，3，5的倍数时达到最佳性能。因此，为了达到最佳性能，通常需要对图像的边界进行填充，使用 getOptimalDFTSize() 和 copyMakeBorder() 进行拓展。

Mat padded;
int m = getOptimalDFTSize(I.rows);
int n = getOptimalDFTSize(I.cols);
copyMakeBorder(I, padded, 0, m - I.rows, 0, n - I.cols, BORDER_CONSTANT, Scalar::all(0));

2. 存储复数和实数
   保留复数，可以通过复数来重新转换到空间域。

 Mat planes[] = {Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F)};
 Mat complexI;
 merge(planes, 2, complexI); // Add to the expanded another plane with zeros

3. 做离散傅里叶变换

 dft(complexI, complexI); // this way the result may fit in the source matrix

4. 将实值和复值转换为图像强度值
   
   复数由实部和虚部组成，在图像处理和傅里叶变换中，复数表示在频域中的图像信息。

 split(complexI, planes); // planes[0] = Re(DFT(I), planes[1] = Im(DFT(I))
 magnitude(planes[0], planes[1], planes[0]);// planes[0] = magnitude
 Mat magI = planes[0];

5. 切换到对数刻度
   结果是傅里叶系数的动态范围太大，无法在屏幕上显示。我们有一些小的和大的变化值我们不能像这样观察到。因此，高值将全部显示为白色点，而小的则显示为黑色点。为了使用灰度值进行可视化，我们可以将线性刻度转换为对数刻度:
   

 magI += Scalar::all(1); // switch to logarithmic scale
 log(magI, magI);

6. 裁剪和重新排列
   由于我们在一开始就拓展了图像，现在是时候将新引入的值去掉。为了可视化的目的，我们还可以重新排列结果的象限，使原点(0,0)与图像中心对应。

 // crop the spectrum, if it has an odd number of rows or columns
 magI = magI(Rect(0, 0, magI.cols & -2, magI.rows & -2));
 
 // rearrange the quadrants of Fourier image so that the origin is at the image center
 int cx = magI.cols/2;
 int cy = magI.rows/2;
 
 Mat q0(magI, Rect(0, 0, cx, cy)); // Top-Left - Create a ROI per quadrant
 Mat q1(magI, Rect(cx, 0, cx, cy)); // Top-Right
 Mat q2(magI, Rect(0, cy, cx, cy)); // Bottom-Left
 Mat q3(magI, Rect(cx, cy, cx, cy)); // Bottom-Right
 
 Mat tmp; // swap quadrants (Top-Left with Bottom-Right)
 q0.copyTo(tmp);
 q3.copyTo(q0);
 tmp.copyTo(q3);
 
 q1.copyTo(tmp); // swap quadrant (Top-Right with Bottom-Left)
 q2.copyTo(q1);
 tmp.copyTo(q2);

7. 归一化
   再次这样做是为了可视化。我们现在有了大小，但是它仍然在0到1的图像显示范围之外。我们使用**cv::normalize()**函数将值规范化到这个范围。

 normalize(magI, magI, 0, 1, NORM_MINMAX); // Transform the matrix with float values into a
 // viewable image form (float between values 0 and 1).

应用示例：确定图像中的几何方向

我们可以利用傅里叶变换来确定图像中的几何方向。例如，我们可以判断文本是否是水平的。观察一些文本时，你会注意到文本行形成了水平线，而字母形成了垂直线。这两个主要组成部分也可以在傅里叶变换的结果中看到。我们可以使用水平和旋转的文本图像来实现这一点。

水平方向

旋转方向

可以看到，频域最具影响力的分量(星等图像上最亮的点)遵循图像上物体的几何旋转。由此，我们可以计算偏移量并执行图像旋转以纠正最终的未对准。