在 Python 中,可以使用数值模拟来研究气体扩散。
模拟气体扩散需要解决两个问题:流体动力学方程(如 Navier-Stokes 方程)和扩散方程。
文章目录
- Python 代码模拟气体扩散
- 计算并显示气体浓度的均值和标准差
- 研究气体扩展的高级方法
Python 代码模拟气体扩散
在进行模拟时,可以使用预定义的数学模型和算法,或者使用框架,如 FEniCS,FiPy 等。
以下是一个简单的 Python 代码演示如何使用数值模拟研究气体扩散:
import numpy as np
import matplotlib.pyplot as plt
Nx = 100
Ny = 100
Lx = 1
Ly = 1
dx = Lx / Nx
dy = Ly / Ny
x = np.linspace(0, Lx, Nx)
y = np.linspace(0, Ly, Ny)
X, Y = np.meshgrid(x, y)
# 初始条件
C = np.zeros((Nx, Ny))
C[Nx // 2, Ny // 2] = 1
# 时间步长和时间步长数
dt = 0.00001
Nt = 10000
# 扩散系数
D = 0.1
# 求解扩散方程
for n in range(Nt):
Cn = C.copy()
C[1:-1, 1:-1] = Cn[1:-1, 1:-1] + D * dt / dx**2 * (Cn[2:, 1:-1] - 2 * Cn[1:-1, 1:-1] + Cn[:-2, 1:-1]) + \
D * dt / dy**2 * (Cn[1:-1, 2:] - 2 * Cn[1:-1, 1:-1] + Cn[1:-1, :-2])
plt.imshow(C, extent=[0, Lx, 0, Ly], origin='lower', cmap='hot')
plt.colorbar()
plt.show()
运行代码得到下述绘图。
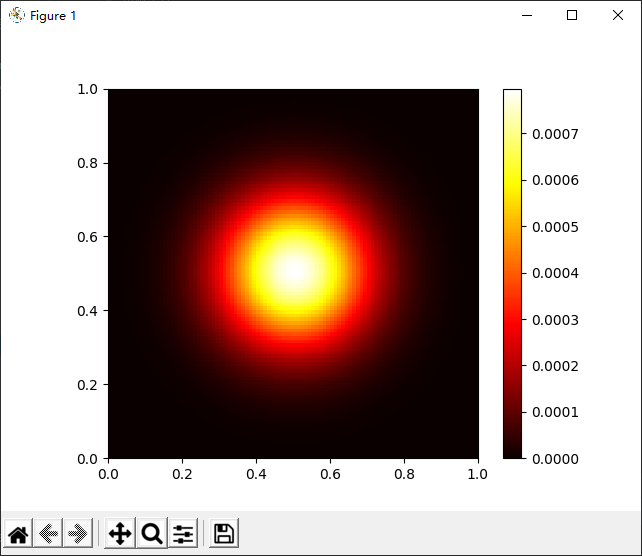
上面的代码演示了如何模拟气体扩散的简单示例。
- 先定义网格和初始条件
- 然后迭代地解决扩散方程
- 最后,使用 Matplotlib 显示气体扩散的分布情况。
计算并显示气体浓度的均值和标准差
可以扩展上面的代码以实现更多功能。例如,可以计算并显示气体浓度的均值和标准差,以了解气体扩散的情况。
import numpy as np
import matplotlib.pyplot as plt
Nx = 100
Ny = 100
Lx = 1
Ly = 1
dx = Lx / Nx
dy = Ly / Ny
x = np.linspace(0, Lx, Nx)
y = np.linspace(0, Ly, Ny)
X, Y = np.meshgrid(x, y)
# Initial conditions
C = np.zeros((Nx, Ny))
C[Nx // 2, Ny // 2] = 1
dt = 0.00001
Nt = 10000
D = 0.1
for n in range(Nt):
Cn = C.copy()
C[1:-1, 1:-1] = Cn[1:-1, 1:-1] + D * dt / dx ** 2 * (Cn[2:, 1:-1] - 2 * Cn[1:-1, 1:-1] + Cn[:-2, 1:-1]) + \
D * dt / dy ** 2 * (Cn[1:-1, 2:] - 2 * Cn[1:-1, 1:-1] + Cn[1:-1, :-2])
mean = np.mean(C)
std = np.std(C)
print("Mean:", mean)
print("Standard deviation:", std)
plt.imshow(C, extent=[0, Lx, 0, Ly], origin='lower', cmap='hot')
plt.colorbar()
plt.show()
运行代码效果图如下所示:
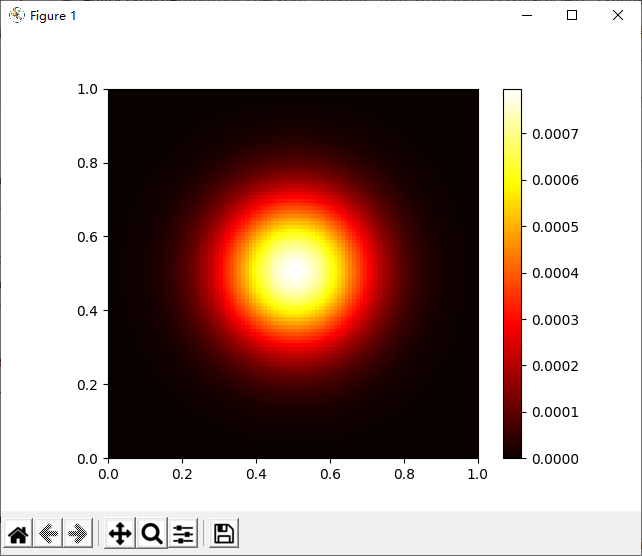
研究气体扩展的高级方法
对于模拟气体扩散,一种常用的更高级方法是使用有限差分方法。
有限差分方法是一种数值模拟方法,用于通过在网格上插值,并使用已知的数值来求解微分方程。
- 常用的有限差分方法包括:
- 差分:一种最简单的有限差分方法,用于模拟气体扩散。
- 积分差分:用于模拟非线性的气体扩散问题。
- 正解差分:用于模拟复杂的气体扩散问题,并且需要更多的计算时间和计算资源。
在 Python 中,可以使用 Scipy 库中的 scipy.sparse 和 scipy.sparse.linalg 模块来实现有限差分方法。
下面是一个使用正解差分模拟气体扩散的示例代码:
import numpy as np
import matplotlib.pyplot as plt
# Parameters
nx = 51
ny = 51
nt = 50
dx = 2 / (nx - 1)
dy = 2 / (ny - 1)
sigma = .2
dt = sigma * dx
x = np.linspace(0, 2, nx)
y = np.linspace(0, 2, ny)
u = np.ones((ny, nx))
v = np.ones((ny, nx))
# Initial Conditions
u[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2
v[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2
for n in range(nt + 1):
un = u.copy()
vn = v.copy()
u[1:, 1:] = (un[1:, 1:] - (un[1:, 1:] * dt / dx * (un[1:, 1:] - un[1:, :-1])) -
vn[1:, 1:] * dt / dy * (un[1:, 1:] - un[:-1, 1:]))
v[1:, 1:] = (vn[1:, 1:] - (un[1:, 1:] * dt / dx * (vn[1:, 1:] - vn[1:, :-1])) -
vn[1:, 1:] * dt / dy * (vn[1:, 1:] - vn[:-1, 1:]))
u[0, :] = 1
u[-1, :] = 1
u[:, 0] = 1
u[:, -1] = 1
v[0, :] = 1
v[-1, :] = 1
v[:, 0] = 1
v[:, -1] = 1
fig = plt.figure(figsize=(11, 7), dpi=100)
ax = fig.gca(projection='3d')
X, Y = np.meshgrid(x, y)
ax.plot_surface(X, Y, u, cmap='viridis')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
这段代码是使用 Python 来模拟气体扩散的例子。代码使用了 NumPy 和 Matplotlib 库:
- NumPy:提供了处理多维数组的工具,本代码中用于创建网格数组并进行数值计算。
- Matplotlib:提供了绘图功能,用于可视化模拟的结果。
代码中首先设置了一些模拟参数,如网格点数、模拟步数、步长和时间步长等。然后使用 linspace() 函数创建网格点的横纵坐标。接着,通过对模拟初始条件的设置,创建了模拟的初始速度场和密度场。最后,代码实现了一个循环,使用正解差分来模拟气体扩散的过程,并使用 Matplotlib 可视化模拟的结果。