写在正文之前
在上一篇文章就说会在这两天会基于PID写一个文章,这里的原理部分值得大家都看一下,代码部分的实现是基于python的,但是对于使用其他编程语言的朋友,由于我写的很通俗易懂,所以也值得借鉴。
一、PID算法介绍
1、开环控制和闭环控制
开环控制和闭环控制的区别在于开环控制没有反馈调节,而闭环控制有反馈调节
PID就是闭环调节
2、PID的标准公式
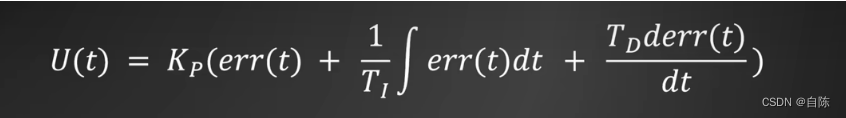
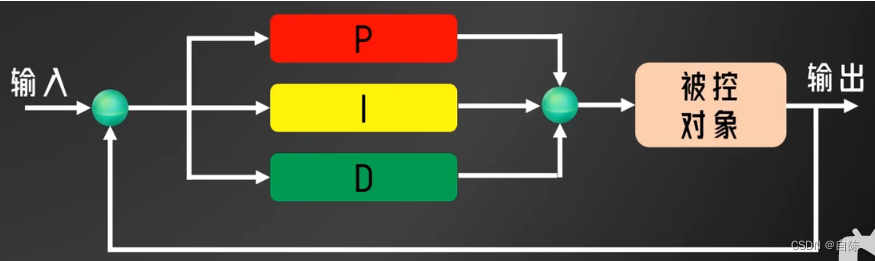
3、PID的控制示意图
4、以无人机场景对PID各部分进行说明
(1)比例控制及稳态误差的存在
Proportion 比例控制
情景:无人机停在两米的高度,我们需要它停在十米的高度
Err = h - h0 =8
比例控制就是每次调节的高度是误差的Kp倍
假设Kp=0.5
Kp * err=4
则第一次调节的量是四米,第二次是两米,随着误差的减小,每次调节上升的量也逐渐减小
最终会接近十米高度,这整个过程就是比例控制
Kp越大,无人机调节越快
但是比例调节也存在弱点,假设无人机到达八米之后,存在一个向下的气流让它下降一米,这时它就会在八米的位置不变
这就是静态误差也叫稳态误差
(2)积分控制与过冲
Integration 积分控制
为了消除稳态误差,我们就要引入积分控制
积分控制是对过去的所有误差求和,在离散的情况,就是做累加
Ki:积分系数
此时的调节函数:Kp * err + Ki * err的积分
假设积分系数为0.1,则在比例控制中出现的稳态误差得到解决,在八米时尽管有向下的气流无人机还是能上升1.2米
经过三次控制,累计误差已经到达了12.8,此时再进行下一次控制就会超过十米,这种现象叫过冲
此时就该微分控制出场了
(3)微分控制
Differential 微分控制
微分控制就是通过当前时刻与前一时刻误差量的差值对未来作预测
如果差值为正,就认为误差在逐渐扩大,需要加大控制强度使误差降下来
如果差值为负,则误差在减小,控制强度可以小一点让目标平稳缓和的到达指定值
二、代码实现过程说明
1、模块的导入
from pyb import millis
from math import pi, isnanmillis用于获取当前的时间,以毫秒为单位
pi是圆周率常数
isnan函数用于检查一个值是否为NAN(Not a Number)
2、定义PID类
class PID:
_kp = _ki = _kd = _integrator = _imax = 0
_last_error = _last_derivative = _last_t = 0
_RC = 1/(2 * pi * 20)
这里定义了PID类的属性,包括
比例、积分、微分系数:_kp、_ki、_kd
积分器:_integrator(用于累积误差,用于计算积分项)
积分限制:_imax
最后的误差:_last_error
最后的导数:_last_derivative(这里的导数值指的是误差随时间的变化率,是通过计算当前误差与前一次误差之差再除以时间间隔得到的)
最后的时间戳:_last_t
RC 低通滤波器的时间常数
3、类中的初始化方法
def __init__(self, p=0, i=0, d=0, imax=0):
# 初始化 PID 控制器的参数
self._kp = float(p) # 比例系数
self._ki = float(i) # 积分系数
self._kd = float(d) # 微分系数
self._imax = abs(imax) # 积分限制,防止积分饱和
self._last_derivative = float('nan') # 最后的导数值初始化为 NaN关于这些参数的说明,在注释中已经给出,我这里只介绍它这里涉及的语法知识
在这里我们可以看到定义变量的时候在变量面前加上了self,请注意,在类中的方法与普通函数区别,类中方法必须有一个额外的第一个参数名称,按照惯例这个名称是“self”
abs函数是取绝对值的函数
4、重置函数
def reset_I(self):
self._integrator = 0 # 重置积分器
self._last_derivative = float('nan') # 重置最后的导数值为 NaN
虽然我这里说的是函数,但是更准确的表达应该是方法
这个类方法重置了积分器(误差的积累值)、 导数值(误差的变化率)
5、PID调节值计算函数
这个部分是整个PID类的重点,作PID的调节,主要就是这个函数
(1)函数的定义及参数的传入
def get_pid(self, error, scaler)
对传入的三个参数进行解释,其中self是调用变量需要的,其他的都是在之后计算涉及到的参数
self:self参数是必须传入的,只有传入了self参数才能使用以self开头的变量
error:误差值
scaler:缩放因子
(2)获取时间、时间差并初始化输出值
tnow = millis() # 获取当前时间
dt = tnow - self._last_t # 计算时间差
output = 0 # 初始化输出值
这里利用了millis函数获取当前时间戳,和上一次获取的时间戳相减得到时间差, 有很多操作都涉及到了时间差
(3)判断是否第一次运行及时间差是否过长
if self._last_t == 0 or dt > 1000:
dt = 0
self.reset_I()
如果是第一次运行或者运行时间过长,我们就重置时间差、积分器、导数值
积分器:误差的累积 导数值:误差的变化率(怕大家看到这里忘了再强调一下)
这里之所以作这样的处理,是因为积分和微分的处理都和之前的状态有关,所以在时间过长的时候我们直接就重置积分器和导数值(它们中存储的信息不再具有实时性)
(4)更新时间戳
self._last_t = tnow # 更新最后时间戳
delta_time = float(dt) / float(1000) # 将时间差转换为秒
这里在更新最后的时间差的同时将时间差转换成秒,方便之后的运算
(5)PID操作
在这里的PID操作要做的事情就是对系数和数据进行运算并将相关值赋给output最后进行输出
PID操作的顺序一般是(如果三个部分都用上):P——>D——>I(比例、微分、积分)
P操作
output += error * self._kp 比例项的处理是最简单的,只需要给误差乘上一个比例系数之后赋值给output
D操作
D操作和I操作就比P操作复杂很多了
我们要根据微分系数的值和时间差的值来进行判断决定下一步的处理
if abs(self._kd) > 0 and dt > 0: # 如果微分系数绝对值大于 0 且时间差大于 0
if isnan(self._last_derivative): # 如果最后的导数值为 NaN,就对其作初始化
derivative = 0 # 导数值设置为 0
self._last_derivative = 0 # 重置最后的导数值
else:
derivative = (error - self._last_error) / delta_time # 计算导数值(误差的变化率)
# 使用低通滤波器平滑导数值
derivative = self._last_derivative + ((delta_time / (self._RC + delta_time)) * (derivative - self._last_derivative)) #delta_time就是转换成秒的时间差
self._last_error = error # 更新最后的误差值
self._last_derivative = derivative # 更新最后的导数值
output += self._kd * derivative # 计算微分项并加到输出中
首先如果微分系数大于0且时间差大于零才进行判断
进入判断之后再对导数值进行判断
如果导数值已经初始化,就计算导数值,如果导数值未进行初始化,就对导数值进行初始化
对导数值的计算首先只是差值减去时间,但是利用低通滤波器平滑导数值
然后就是顺便更新最后的导数值和误差值,然后把通过低通滤波之后的导数值乘以微分项加到output中
I操作
如果给出代码,大家可能会发现有一点很奇怪,那就是在我们进行积分操作之前有一个缩放操作
output *= scaler 这个缩放值一般是1,当然,根据情况可以赋不同的值来适应不同的控制系统需求和误差幅度
接下来才是I操作,积分操作和微分操作的逻辑很像
if abs(self._ki) > 0 and dt > 0:
self._integrator += (error * self._ki) * scaler * delta_time
if self._integrator < -self._imax:
self._integrator = -self._imax
elif self._integrator > self._imax:
self._integrator = self._imax
output += self._integrator
首先对微分系数和时间差进行判断,若积分系数不为0且时间差大于零,进入分支
分支中的处理代码的主要功能是把积分器的值在-imax和imax之间,防止积分饱和
在作完了防止积分饱和的代码之后,我们把积分器也加入到output中,最后将output的值返回,这就是我们的最后调控PID控制函数返回的值
return output(6)完整代码附上
from pyb import millis # 导入 pyboard 的 millis 函数,用于获取当前时间(毫秒)
from math import pi, isnan # 导入 pi 和 isnan 函数
class PID:
# 定义 PID 控制器的参数和状态变量
_kp = _ki = _kd = _integrator = _imax = 0
_last_error = _last_derivative = _last_t = 0
_RC = 1/(2 * pi * 20) # RC 低通滤波器的时间常数
def __init__(self, p=0, i=0, d=0, imax=0):
# 初始化 PID 控制器的参数
self._kp = float(p) # 比例系数
self._ki = float(i) # 积分系数
self._kd = float(d) # 微分系数
self._imax = abs(imax) # 积分限制,防止积分饱和
self._last_derivative = float('nan') # 最后的导数值初始化为 NaN
def get_pid(self, error, scaler):
tnow = millis() # 获取当前时间
dt = tnow - self._last_t # 计算时间差
output = 0 # 初始化输出值
if self._last_t == 0 or dt > 1000: # 如果是第一次运行或者时间差大于 1 秒
dt = 0 # 重置时间差
self.reset_I() # 重置积分器
self._last_t = tnow # 更新最后时间戳
delta_time = float(dt) / float(1000) # 将时间差转换为秒
output += error * self._kp # 计算比例项
if abs(self._kd) > 0 and dt > 0: # 如果微分系数大于 0 且时间差大于 0
if isnan(self._last_derivative): # 如果最后的导数值为 NaN
derivative = 0 # 设置导数为 0
self._last_derivative = 0 # 重置最后的导数值
else:
derivative = (error - self._last_error) / delta_time # 计算误差的导 数
# 使用低通滤波器平滑导数值
derivative = self._last_derivative + ((delta_time / (self._RC + delta_time)) * (derivative - self._last_derivative))
self._last_error = error # 更新最后的误差值
self._last_derivative = derivative # 更新最后的导数值
output += self._kd * derivative # 计算微分项并加到输出中
output *= scaler # 按比例缩放输出值
if abs(self._ki) > 0 and dt > 0: # 如果积分系数大于 0 且时间差大于 0
self._integrator += (error * self._ki) * scaler * delta_time # 计算积分项并加到积分器中
# 限制积分器的值在 -imax 和 imax 之间,防止积分饱和
if self._integrator < -self._imax:
self._integrator = -self._imax
elif self._integrator > self._imax:
self._integrator = self._imax
output += self._integrator # 将积分项加到输出中
return output # 返回计算的 PID 控制器输出值
def reset_I(self):
self._integrator = 0 # 重置积分器
self._last_derivative = float('nan') # 重置最后的导数值为 NaN