Background

yolov10是清华大学发布的一个新yolo算法，作者认为NMS是影响yolo实时推理的一个主要问题，针对这个问题提出了dual assignments的方法来训练NMS-free的yolo模型。同时作者从速度和精度入手，提出了几个改进模型的方法。yolov10在推理速度以及参数量上都优于现有的模型，且仍具有不弱于其他模型的精度。接下来主要分析yolov10中的dual asignments和 Efficiency-Accuracy优化策略。

yolov10的论文地址：https://arxiv.org/abs/2405.14458
yolov10的代码地址：https://github.com/THU-MIG/yolov10

Consistent Dual Assignments for NMS-free Training

作者认为one-to-many label assign需要NMS进行后处理，从而影响模型部署后的推理速度，然而one-to-one label assign会带来额外的推理开销并且没有太好的表现。
基于这俩个原因，提出了dual label assignmets的策略，即在yolo中同时采用one-one和one-to-many。模型的结构见下图

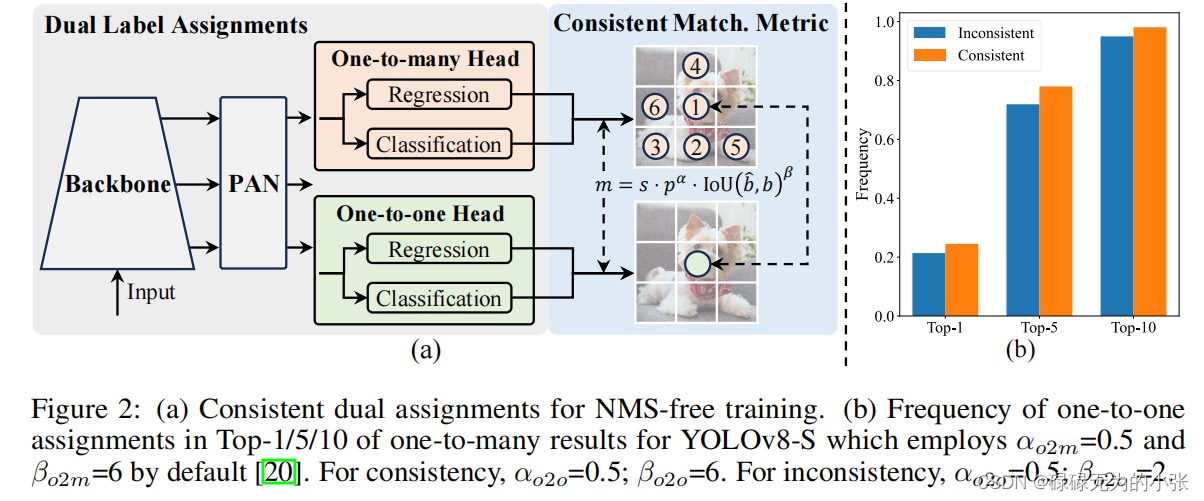
从上图可以看出，相较于普通的yolo头，这里的yolo头有俩个，分别用于one-to-one和one-to-many。同时每个头都采用了解耦头的方式，即回归和分类分开。这里的思想跟v7中的辅助头是挺像的，通过一个aux head实现one-to-many，lead head实现one-to-one。最后在推理阶段丢弃aux head。

引入了俩个头之后，最大的问题就是如何去分配标签。这里作者对俩个头都用了一样的匹配度量。这里匹配度量的仍然是考虑了分类头和回归头，这里匹配损失记为$m$，具体计算如下$$m(\alpha ,\beta )=s\cdot p^{\alpha }\cdot IOU(\hat{b},b{)}^{\beta }$$其中$p$是指分类分数，$\hat{b}$为预测框，$b$为真实框，$\alpha$和$\beta$是超参数。
这样度量就同时考虑了分类任务和回归任务。对于one-to-one的任务记为$m_{o2o}=m_{o2o}({\alpha }_{o2o},{\beta }_{o2o})$，对于one-to-many的任务记为$m_{o2m}=m_{o2m}({\alpha }_{o2m},{\beta }_{o2m})$。

作者认为o2m能够提供更丰富的监督信息，同时希望o2m能够引导o2o。所以作者分析了o2o和o2m的差距，发现它们在回归任务上的表现没什么大的差异，所以认为它们的差距主要体现在分类任务上。然后就是针对分类任务进行改进。

先给定一个目标，然后记俩个头预测的最大IOU为$u^{\ast }$(由于回归任务差不多，所任可以认为俩个头预测的最大IOU相等)，然后记俩个头的最大匹配分数为$m_{o2o}^{\ast }$和$m_{o2m}^{\ast }$。

同时假设$o2m$的最佳匹配为$\Omega$，而$o2o$的最佳匹配为第$i$个，并记为$m_{o2o,i}=m_{o2o}^{\ast }$。然后有以下的等式关系$$\begin{array}{rl}{t}_{o2m,j}=& u^{\ast }\frac{m_{o2m,j}}{m_{o2m}^{\ast }}\le u^{\ast }\\ t_{o2o,i}=& u^{\ast }\frac{m_{o2o,i}}{m_{o2o}^{\ast }}=u^{\ast }\end{array}$$这里的等式是采取了跟TOOD中类似的归一化度量，首先这里认为分类损失匹配$t_{o2o|o2m}$跟$m_{o2o|o2m}$是等价的（这里不能用公式中的$p$来看做$t$）。然后借助TOOD中的归一化方法处理$m$，即$norm(u)=\max (iou)\ast \frac{u}{\max (u)}$。

然后定义了俩个头的差距用 1-Wasserstein distance表示，具体为 A = t o 2 o , i − 1 i ∈ Ω t o 2 m , i + ∑ k ∈ Ω ∖ { i } t o 2 m , k A =t_{o2o,i}-1_{i\in\Omega}t_{o2m,i}+\sum_{k\in{\Omega}\setminus \{i\}}t_{o2m,k} A=to2o,i​−1i∈Ω​to2m,i​+k∈Ω∖{i}∑​to2m,k​直观地说，这个公式是使$t_{o2o}$越来越接近$t_{o2m}$。同使$t_{o2m,i}$尽可能地大（这里有点奇怪，不过合理的解释是当A的权重不大时，这里可以使$t_{o2o,i}$接近$t_{o2m,i}$，使$t_{o2o,k}$稍微抑制使其变小）

具体上，作者是对one2one和one2many都采用了TAL作为分配策略，但是对one2one采用top1，对one2many采用top10。这里v10是延续了v8的分配方式。

class v10DetectLoss:
    def __init__(self, model):
        self.one2many = v8DetectionLoss(model, tal_topk=10)
        self.one2one = v8DetectionLoss(model, tal_topk=1)
    
    def __call__(self, preds, batch):
        one2many = preds["one2many"]
        loss_one2many = self.one2many(one2many, batch)
        one2one = preds["one2one"]
        loss_one2one = self.one2one(one2one, batch)
        return loss_one2many[0] + loss_one2one[0], torch.cat((loss_one2many[1], loss_one2one[1]))

在源码中没有找到对齐损失1-Wasserstein distance的实现(有读者发现的话可以在评论说一下)。其余的loss function跟v8类似，就是引入了一个one2many。

Holistic Efficiency-Accuracy Driven Model Design

作者认为yolo架构存在较多的计算冗余，这样会阻碍它的能力。所以作者希望在速度和精度俩个方面对模型进行改进。

Efficiency driven model design

作者认为在yolo中下采样、basic building blocks和头部三个部分对速率影响较大。所以分别对这三部分进行改进。

Lightweight classification head

第一个是头部进行改进，作者通过实验验证了改进回归头对模型的表现影响较大，然后分类头的参数和计算量是回归头的俩倍多，所以作者使用了俩个深度可分离卷积（ depthwise separable convolutions）替代了原来的分类头。具体代码如下

self.cv3 = nn.ModuleList(nn.Sequential(nn.Sequential(Conv(x, x, 3, g=x), Conv(x, c3, 1)), \
                                       nn.Sequential(Conv(c3, c3, 3, g=c3), Conv(c3, c3, 1)), \
                                        nn.Conv2d(c3, self.nc, 1)) for i, x in enumerate(ch))

Spatial-channel decoupled downsampling

第二个是对下采样部分进行改进，简单而言就是用了pointwise convolution和depthwise convolution进行下采样，替代了kernel为3x3且stride为2的卷积。假设对图像大小为$(H\times W\times C)$的图像进行下采样得到$(\frac{H}{2}\times \frac{W}{2}\times C^2)$，在不替换前需要的计算量和参数量分别为$O(\frac{18HW{C}^2}{4})=O(\frac{9HW{C}^2}{2})$和$O(9\ast 2C^2)=O(18C^2)$。

使用pointwise convolution的将其$(H\times W\times C)\to (H\times W\times 2C)$，计算量和参数分别为$O(2HW{C}^2)$和$O(2C^2)$，然后使用3x3的depthwise convolution将其$(H\times W\times 2C)\to (\frac{H}{2}\times \frac{W}{2}\times 2C)$，计算量和参数量分别为$O（\frac{9WH\ast 2C}{4})=O(\frac{9WHC}{2})$和$O(18C)$。所以总的计算量和参数量为$O(2HW{C}^2+\frac{9WHC}{2})$和$O(2C^2+18C)$

总的而言这个方式可以使计算量从$O(\frac{9HW{C}^2}{2})$降至$O(2HW{C}^2+\frac{9WHC}{2})$，参数量从$O(18C^2)$降至$O(2C^2+18C)$。

Rank-guided block design

第三部分是basic building block。作者认为模型在重复使用同个模块拼接后，会带来较大的信息冗余。所以作者对yolov8各个大小的模型的每个阶段的最后一个卷积进行秩的分析，通过下图可以发现模型较大且较深时，秩相对较小。说明了大模型存在较多的信息冗余，也就是说有用的信息不多。所以作者提出了CIB模块，CIB模块由3个3x3的DW卷积和2个1x1的卷积组成，下图展示了将CIB模块嵌入ELAN的方法。作者希望通过CIB模块降低模型的复杂度，同时保证模型的ap值。

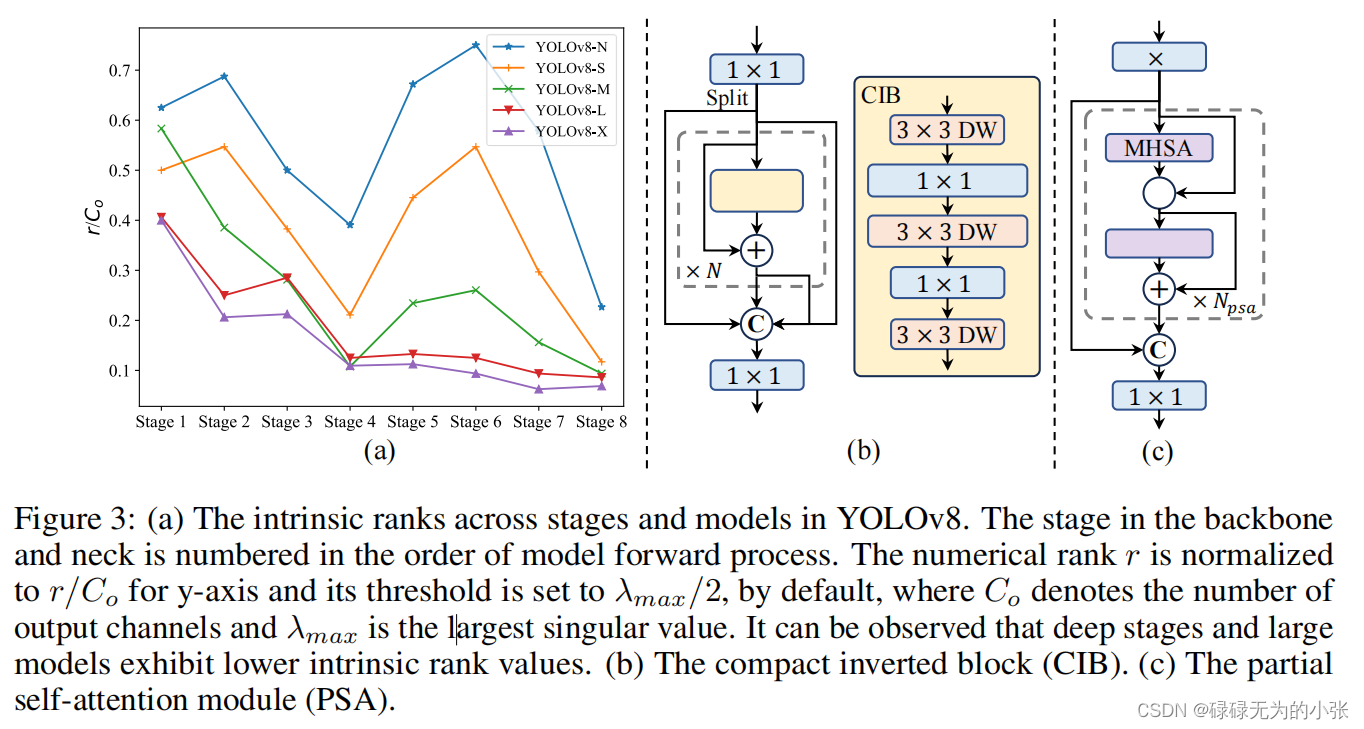
具体的操作方式，就是先训练一个模型，然后对模型的每个阶段进行分析，选取秩最小的那个阶段，插入CIB模块，判断是否能带来AP增益，是的话则继续替换（替换过的不在参加），不然就直接输出。具体的流程如下

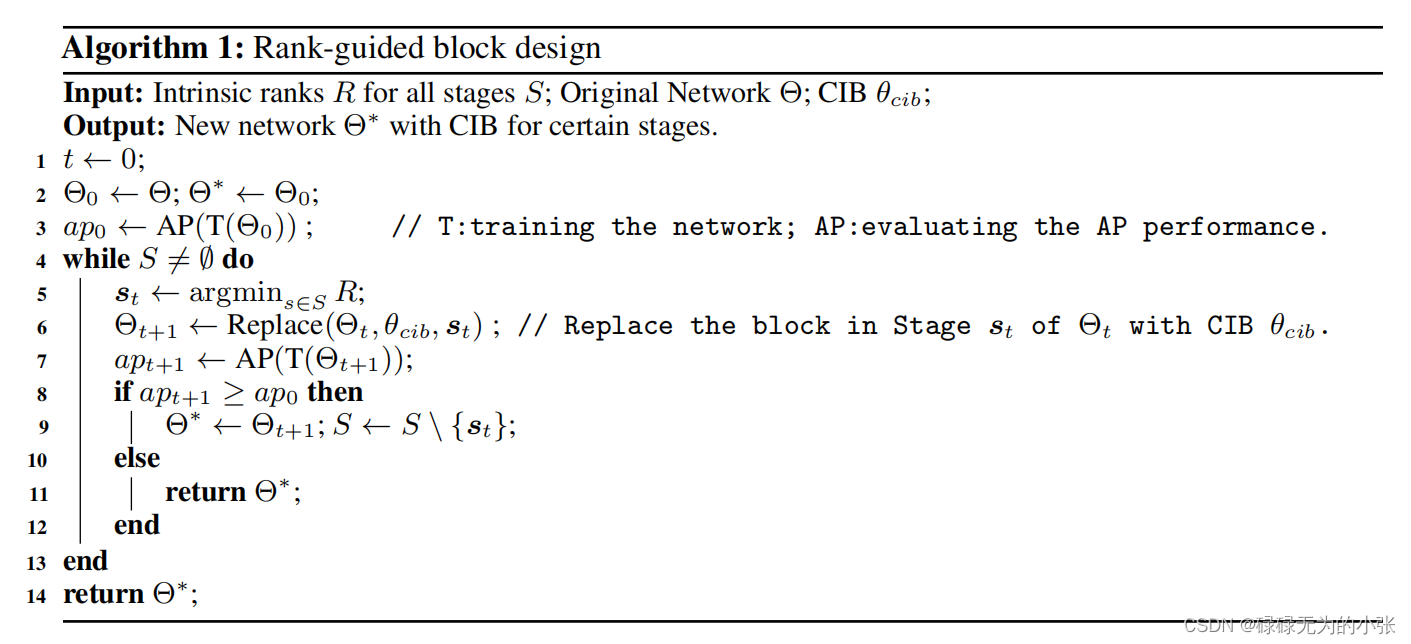
这个方法可以帮助模型降低参数量，同时保持模型的精度。这个思想是值得借鉴的，在许多大参数量的模型中，借助这种方法可以实现参数量的下降。

Accuracy driven model design

作者从大卷积核和self-attention俩个部分提高模型的准确率。

第一部分，作者将CIB模块中第二个$3\times 3$的卷积核换成了7x7，并采用了重参数化的方式，代码部分如下

class RepVGGDW(torch.nn.Module):
    def __init__(self, ed) -> None:
        super().__init__()
        self.conv = Conv(ed, ed, 7, 1, 3, g=ed, act=False)
        self.conv1 = Conv(ed, ed, 3, 1, 1, g=ed, act=False)
        self.dim = ed
        self.act = nn.SiLU()
    
    def forward(self, x):
        return self.act(self.conv(x) + self.conv1(x))
    
    def forward_fuse(self, x):
        return self.act(self.conv(x))

    @torch.no_grad()
    def fuse(self):
        conv = fuse_conv_and_bn(self.conv.conv, self.conv.bn)
        conv1 = fuse_conv_and_bn(self.conv1.conv, self.conv1.bn)
        
        conv_w = conv.weight
        conv_b = conv.bias
        conv1_w = conv1.weight
        conv1_b = conv1.bias
        
        conv1_w = torch.nn.functional.pad(conv1_w, [2,2,2,2])

        final_conv_w = conv_w + conv1_w
        final_conv_b = conv_b + conv1_b

        conv.weight.data.copy_(final_conv_w)
        conv.bias.data.copy_(final_conv_b)

        self.conv = conv
        del self.conv1

class CIB(nn.Module):
    """Standard bottleneck."""

    def __init__(self, c1, c2, shortcut=True, e=0.5, lk=False):
        """Initializes a bottleneck module with given input/output channels, shortcut option, group, kernels, and
        expansion.
        """
        super().__init__()
        c_ = int(c2 * e)  # hidden channels
        self.cv1 = nn.Sequential(
            Conv(c1, c1, 3, g=c1),
            Conv(c1, 2 * c_, 1),
            #lk为true时使用大卷积核
            Conv(2 * c_, 2 * c_, 3, g=2 * c_) if not lk else RepVGGDW(2 * c_),
            Conv(2 * c_, c2, 1),
            Conv(c2, c2, 3, g=c2),
        )

        self.add = shortcut and c1 == c2

    def forward(self, x):
        """'forward()' applies the YOLO FPN to input data."""
        return x + self.cv1(x) if self.add else self.cv1(x)

同时作者主要将其应用小模型上，因为大模型的感受野比较大，卷积核的作用就会比较小。

第二部分是Partial self-attention，其模型结构如下

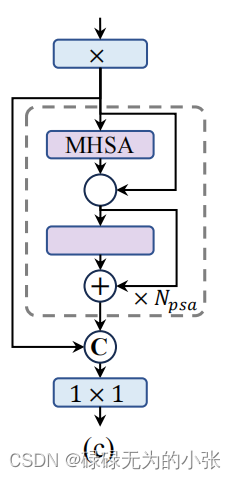
从上述结构图可以看出，其采用了于CSP类似的方法，将输入的$x$用$1\times 1$的卷积后分成俩个部分（有的是直接用1x1的卷积实现）。然后将其中的一部分直接输出至最后，另一部分输入$N_{psa}$模块，并将query和key的channel砍半，显而易见这种方式是能够降低参数量。其他就是正常的self-attention和csp部分了。这部分的代码如下

class Attention(nn.Module):
    def __init__(self, dim, num_heads=8,
                 attn_ratio=0.5):
        super().__init__()
        self.num_heads = num_heads
        self.head_dim = dim // num_heads
        self.key_dim = int(self.head_dim * attn_ratio)
        self.scale = self.key_dim ** -0.5
        nh_kd = nh_kd = self.key_dim * num_heads
        #原本是3*dim，现在变成了2*dim
        h = dim + nh_kd * 2
        self.qkv = Conv(dim, h, 1, act=False)
        self.proj = Conv(dim, dim, 1, act=False)
        self.pe = Conv(dim, dim, 3, 1, g=dim, act=False)

    def forward(self, x):
        B, C, H, W = x.shape
        N = H * W
        qkv = self.qkv(x)
        q, k, v = qkv.view(B, self.num_heads, self.key_dim*2 + self.head_dim, N).split([self.key_dim, self.key_dim, self.head_dim], dim=2)

        attn = (
            (q.transpose(-2, -1) @ k) * self.scale
        )
        attn = attn.softmax(dim=-1)
        x = (v @ attn.transpose(-2, -1)).view(B, C, H, W) + self.pe(v.reshape(B, C, H, W))
        x = self.proj(x)
        return x

class PSA(nn.Module):

    def __init__(self, c1, c2, e=0.5):
        super().__init__()
        assert(c1 == c2)
        self.c = int(c1 * e)
        self.cv1 = Conv(c1, 2 * self.c, 1, 1)
        self.cv2 = Conv(2 * self.c, c1, 1)
        
        self.attn = Attention(self.c, attn_ratio=0.5, num_heads=self.c // 64)
        self.ffn = nn.Sequential(
            Conv(self.c, self.c*2, 1),
            Conv(self.c*2, self.c, 1, act=False)
        )
        
    def forward(self, x):
        a, b = self.cv1(x).split((self.c, self.c), dim=1)
        b = b + self.attn(b)
        b = b + self.ffn(b)
        return self.cv2(torch.cat((a, b), 1))

作者只将这部分用于低分辨率的部分，由于低分辨率的长度$(H\times W)$会比较短，所以这样能够使这块的复杂度不会太高。

Conclusion

yolov10借助了许多轻量化卷积的方法嵌入到模型中，降低模型的参数量和计算量。同时提出了dual assigment的方法用于模型训练，从而实现了NMS-free。个人认为yolov10的意义主要在于其在NMS上的改进。NMS是目标检测模型很难避开的一个算法，当然以前也有许多NMS-free的模型，但是都会面对巨大的计算量或者训练不收敛等问题，