强化学习笔记
第一章 强化学习基本概念
第二章 贝尔曼方程
第三章 贝尔曼最优方程
第四章 值迭代和策略迭代
第五章 强化学习实例分析:GridWorld
第六章 蒙特卡洛方法
第七章 Robbins-Monro算法
第八章 多臂老虎机
第九章 强化学习实例分析:CartPole
第十章 时序差分法
第十一章 值函数近似【DQN】
第十二章 基于强化学习DQN的股票预测
文章目录
- 强化学习笔记
- 一、DQN
- 二、软更新
- 三、实验
- 四、参考资料
在金融决策问题中,如何制定有效的交易策略一直是一个重要且具有挑战性的问题。近年来,强化学习在这一领域的应用显示出了很大的潜力,比如,强化学习可以帮助我们在股票交易过程中进行决策。
在这里,我想先比较一下监督学习和强化学习在股票交易问题中的不同:
- 监督学习主要关注预测,即通过历史数据训练模型,然后对未来的数据进行预测。例如,我们可以通过监督学习预测股票的价格走势。如果要交易还得结合其他策略方法。
- 而强化学习不仅仅是预测,它可以进行交易决策。它不仅仅关注于预测未来的股票价格,更重要的是,它可以根据预测结果来制定买卖策略,以最大化我们的收益。
下图给出了强化学习在股票交易问题应用中的主要框架:
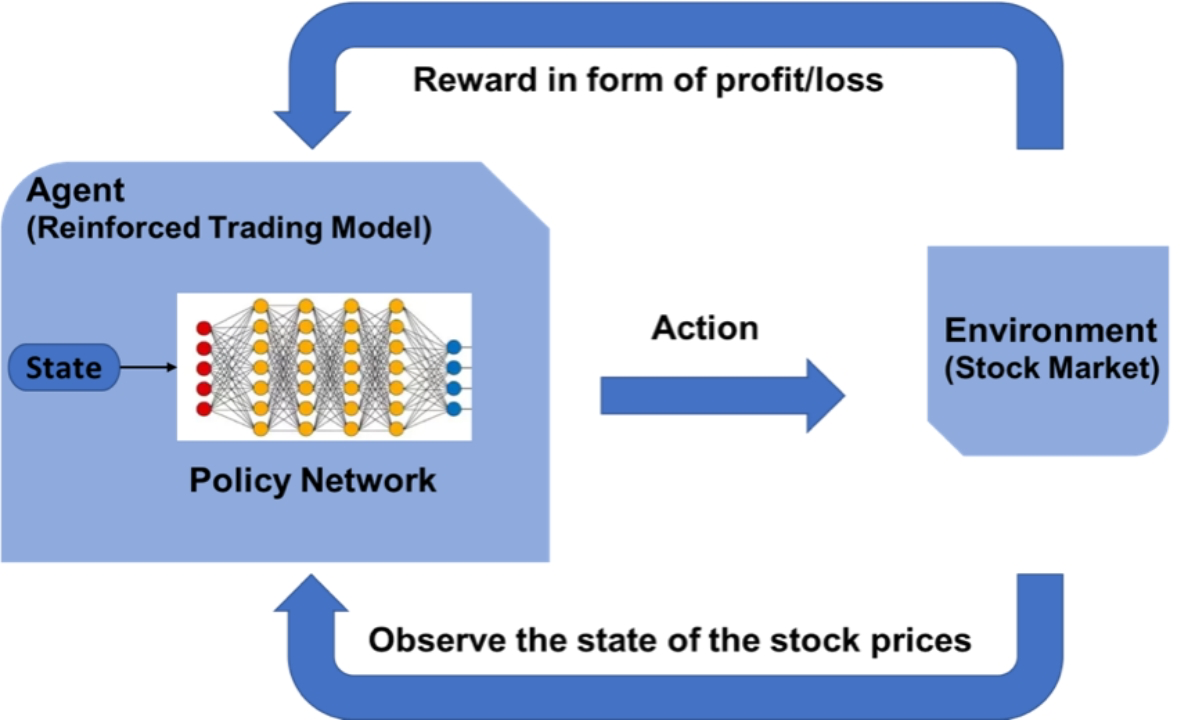 其核心问题有以下几点:
其核心问题有以下几点:
- 如何定义奖励函数,即Reward如何设置?
- 采用强化学习中的哪种模型,DQN、PPO、A2C、DDPG……
- 状态空间如何定义?
一、DQN
本文我们介绍用深度强化学习中最经典的模型——DQN来进行建模,完整代码放在GitHub上——DQN-for-Stock-Trading。在DQN模型中,采用了多个全连接线性层,其模型结构如下:
class QNetwork(nn.Module):
"""QNetwork (Deep Q-Network), state is the input,
and the output is the Q value of each action.
"""
def __init__(self, state_size, action_size, fc1_units=128, fc2_units=128, fc3_units=64):
super(QNetwork, self).__init__()
self.fc1 = nn.Linear(state_size , fc1_units)
self.fc2 = nn.Linear(fc1_units, fc2_units)
self.fc3 = nn.Linear(fc2_units, fc3_units)
self.fc4 = nn.Linear(fc3_units, action_size)
self.dropout = nn.Dropout(0.1) # Dropout with 20% probability
def forward(self, state):
x = F.relu(self.fc1(state))
x = self.dropout(x)
x = F.relu(self.fc2(x))
x = self.dropout(x)
x = F.relu(self.fc3(x))
x = self.fc4(x)
return x
其中:
- 输入也就是状态 s s s,建模为股票过去几天的波动情况,也就是相邻两天的差值,输入的维数由给定的一个滑动窗口大小决定;
- 输出则是action,这里我设置action有三种0、1、2,分别代表买入,卖出或者不变.
DQN的一个核心思想是经验缓冲池,将数据都放入缓冲池内,训练网络时从这里面采样得到小批量数据,其主要代码如下:
class ReplayBuffer:
def __init__(self, action_size, buffer_size, batch_size):
self.action_size = action_size
self.memory = deque(maxlen=buffer_size) # initialize replay buffer
self.batch_size = batch_size
self.experience = namedtuple("Experience", field_names=["state", "action", "reward", "next_state", "done"])
def add(self, state, action, reward, next_state, done):
"""Add a new experience to memory."""
e = self.experience(state, action, reward, next_state, done)
self.memory.append(e)
def __len__(self):
"""Return the current size of internal memory."""
return len(self.memory)
DQN另一个重要思想是用两个神经网络来交替更新参数,其代码如下:
class Agent:
def __init__(self, state_size, action_size):
self.state_size = state_size
self.action_size = action_size
# Q-Network
self.qnetwork_local = QNetwork(state_size, action_size).to(device)
self.qnetwork_target = QNetwork(state_size, action_size).to(device)
self.optimizer = optim.Adam(self.qnetwork_local.parameters(), lr=LR)
二、软更新
在更新target network时,我们采用软更新的策略。软更新是一种在深度强化学习中更新目标网络参数的方法。目标网络(target network)用于稳定训练过程,其参数并不像本地网络(local network)那样在每一步都更新,而是以较慢的速率进行更新。软更新通过将目标网络的参数逐步向本地网络的参数靠拢来实现这种较慢的更新。具体来说,软更新的公式如下:
θ
target
←
τ
θ
local
+
(
1
−
τ
)
θ
target
\theta_{\text{target}} \leftarrow \tau \theta_{\text{local}} + (1 - \tau) \theta_{\text{target}}
θtarget←τθlocal+(1−τ)θtarget其中:
- θ target \theta_{\text{target}} θtarget 是目标网络的参数。
- θ local \theta_{\text{local}} θlocal 是本地网络的参数。
- τ \tau τ 是软更新的比例系数,通常是一个非常小的值(例如 0.001)。
这个公式表示目标网络的参数是本地网络参数的 τ \tau τ 倍加上目标网络自身参数的 ( 1 − τ ) (1 - \tau) (1−τ) 倍。因此,目标网络参数的变化是渐进的,而不是像硬更新(hard update)那样直接将本地网络的参数复制到目标网络。
在代码中,软更新通过 soft_update 方法实现:
def soft_update(self, local_model, target_model, tau):
for target_param, local_param in zip(target_model.parameters(), local_model.parameters()):
target_param.data.copy_(tau * local_param.data + (1.0 - tau) * target_param.data)
在DQN算法中,如果目标网络的参数频繁更新,会导致训练过程不稳定,因为目标网络用于计算目标值,而这些目标值需要在一段时间内保持相对稳定。因此,软更新通过缓慢调整目标网络的参数,能够有效地平滑训练过程,提高算法的收敛性和稳定性。
三、实验
在比较简单的环境设置下进行实验,不考虑交易成本,每次买入卖出都是1股股票,reward设置为卖出股票时赚的钱。下图是训练过程的累积收益,我们可以看到随着不断地学习,agent的决策确实使得我们在这只股票上挣钱了!
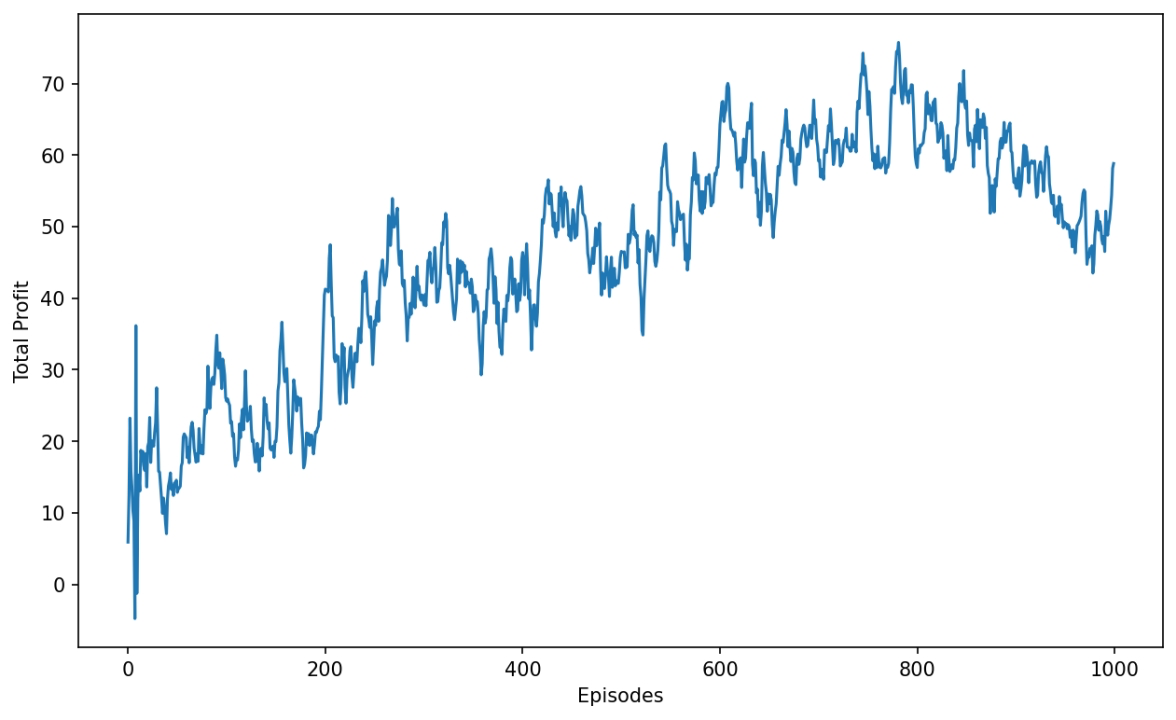
下图是在训练数据上回测的结果,我们可以看到agent学到了一个简单的“低吸高抛”的策略。
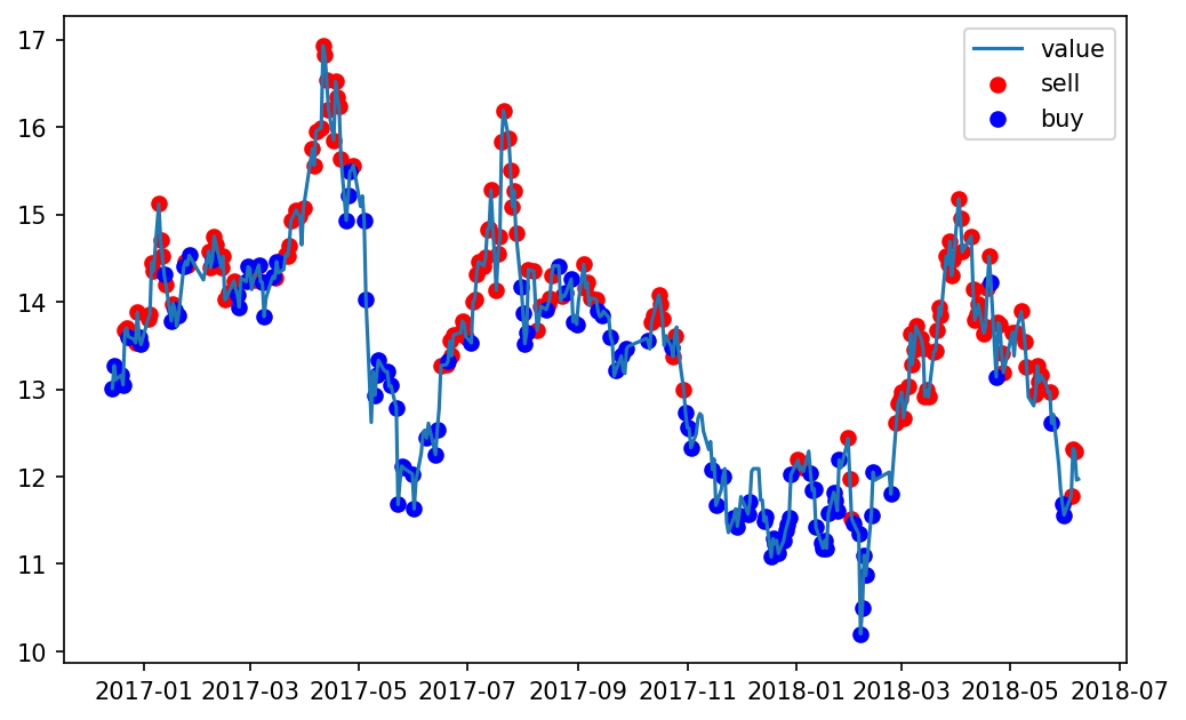
下图是在测试集上的实验,我们发现在没有训练的数据上用刚才的模型也能挣钱,并且策略仍然是低吸高抛.
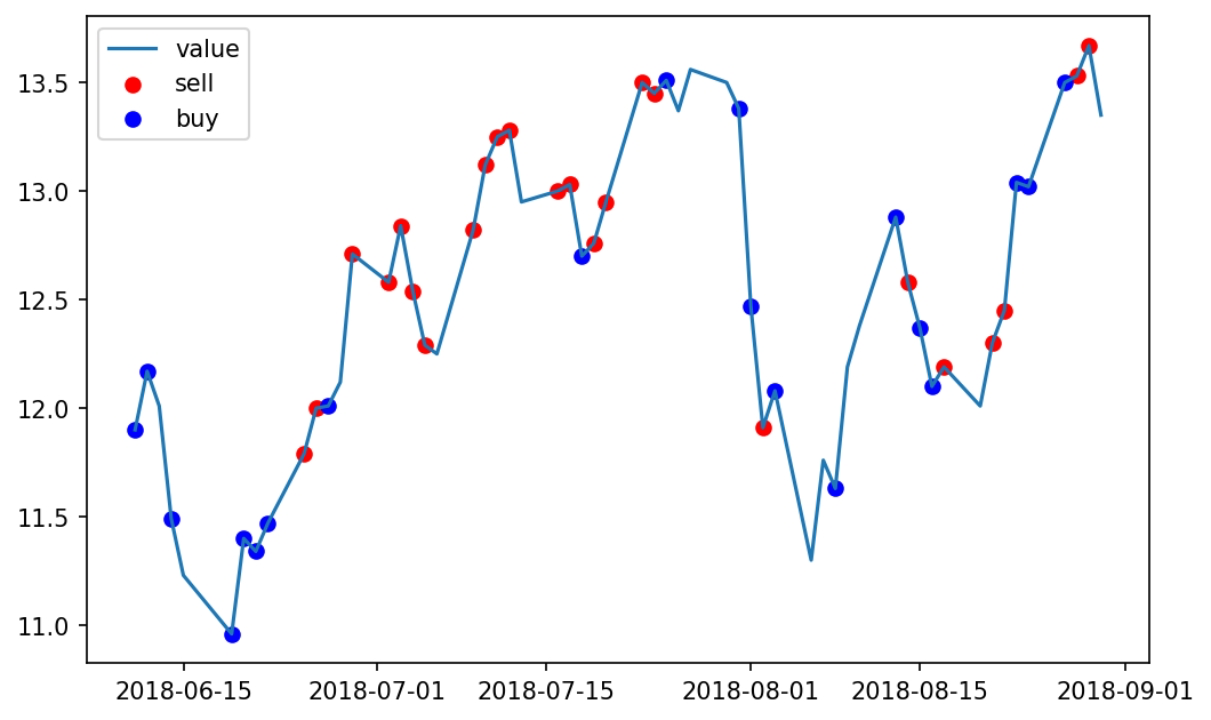
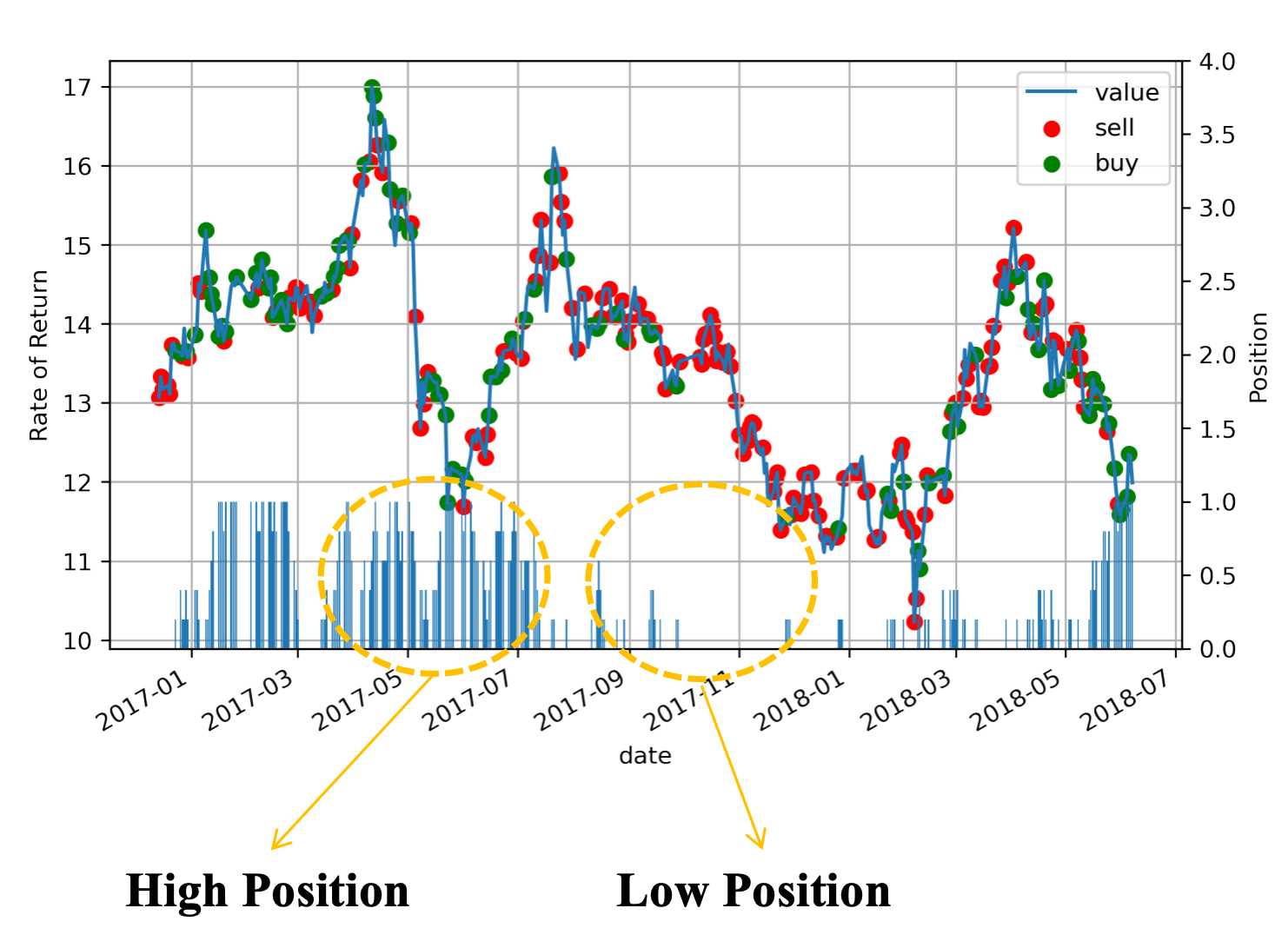
采用更复杂的交易环境,考虑交易成本,每次买入卖出的数量,奖励函数采用收益率,我们可以得到一个复杂的策略。下图图仍是在训练数据上的回测,我们可以看到相比前面的“低吸高抛”策略稍微复杂了一些,下面条形图表示持仓,可以看到学习的策略在股票价格最低时增大仓位,在股票价格高点时,抛售赚钱。
四、参考资料
- https://www.youtube.com/watch?v=05NqKJ0v7EE