位运算算法系列|概念讲解|例题讲解

news2024/11/16 7:28:01

大家好,我是LvZi,今天带来位运算算法系列|概念讲解|例题讲解
在这里插入图片描述

一,位运算基本概念

1.基础位运算

  • <<:左移操作,相当于 *2
  • >>:右移操作,相当于 /2
  • ~:按位取反
  • &:按位与操作,有0则0
  • |:按位或操作,有1则1
  • ^:按位异或操作,相同为0,相异为1/无进位相加

注:对于^操作,无进位相加值得是在相加的过程中不产生进位操作(出现进位也不相/2加)

  • 需要注意的是尽管通过>>1或者<<1来替代/2和*2,会使得程序的运行速度加快,但是由于优先级的问题,会经常出错,其实也不需要考虑优先级的高低,按照自己的逻辑运算先后添加()即可

如何理解^运算的本质是无进位加法呢

  1. 两个二进制正常相加的结果和十进制相加的结果相同
  2. 二进制相加只可能是三种情况0+0,1+0,1+1
  3. 对于前两种情况:0+0 = 0^0 = 0,0+1 = 0^1 = 1,异或的结果和正常相加的结果相同
  4. 对于最后一种情况,虽然1+1 = 1^1 = 0,但是对于正常的二进制相加,会存在进位,对于^操作,不存在进位,也不会向前进位
  5. 综上,^被称为无进位加法

2.位图

给一个数n,判断 第x位数字是0/1

核心公式:n &= (1 << x),设最后的结果为ret

  • ret == 0 则x == 0
  • ret == 1 则 x == 1

注意:对于一个32位的数字,最右边的下标我们设为0,这样方便进行移位操作

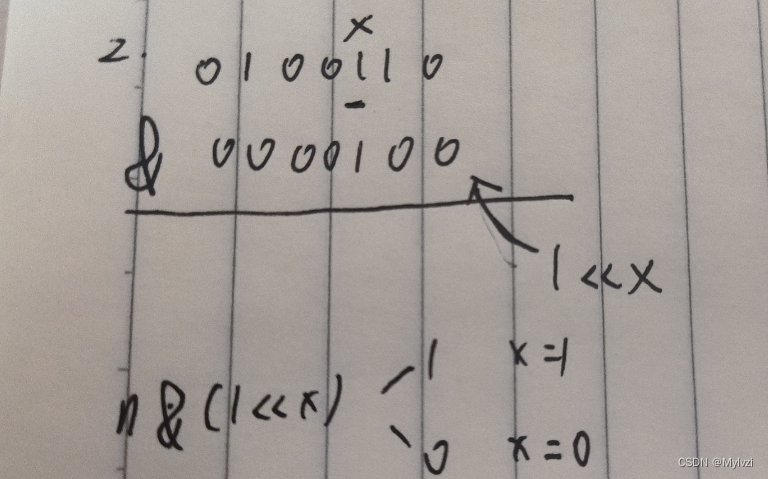
在这里插入图片描述

给一个数n,将第x位修改为1,其余位保持不变

核心公式:n |= (1 << x)

可以这么想,既然要出现1,想想哪个位运算操作容易出现1?当然是|操作,因为按位或是有1则1,特别容易出现1,所以使用|操作,将第x位设置为1,就让1 << x位
在这里插入图片描述

给一个数n,将第x位修改为0

核心公式:n &= ~(1 << x)

和上述想法一致,&操作出现0的概率更大,所以使用&操作,让第x位和0 &操作,一定能出现0,其余位都设置为1
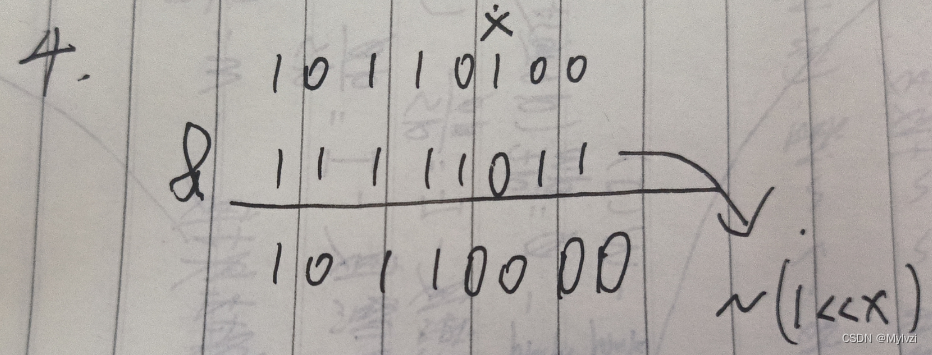
在这里插入图片描述

让二进制位不发生改变的算法:&1或者|0

位图

对于一个整数来说,其本质上是一个32位的二进制数,位图思想就是利用这32个0,1数字来存储信息的一种方式

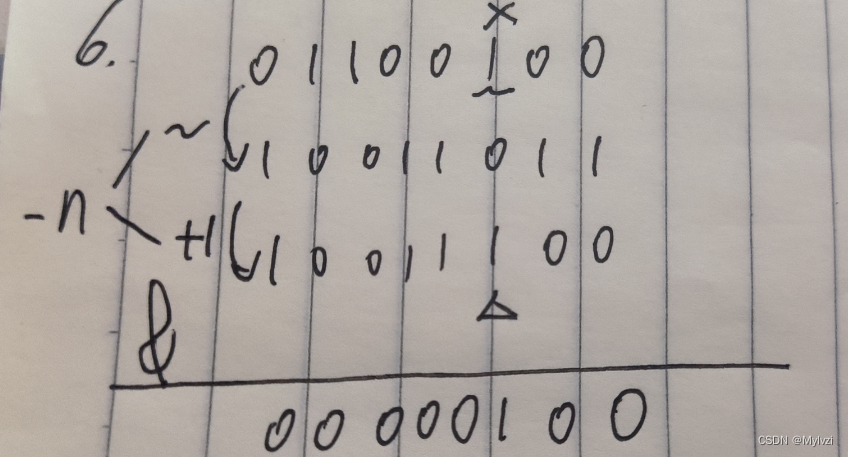
给定一个数n,提取最右侧的1(Lowbit)

核心公式:n & (-n)

n -> (-n),分为两步:

  1. 按位取反 ~
  2. 加一

-n的操作实际上是把n中最右侧的1的左边区域全部取反,右侧保持不变(全是0),1仍是1

所以让(-n)和n进行&,左侧全部变为0右侧也全是0
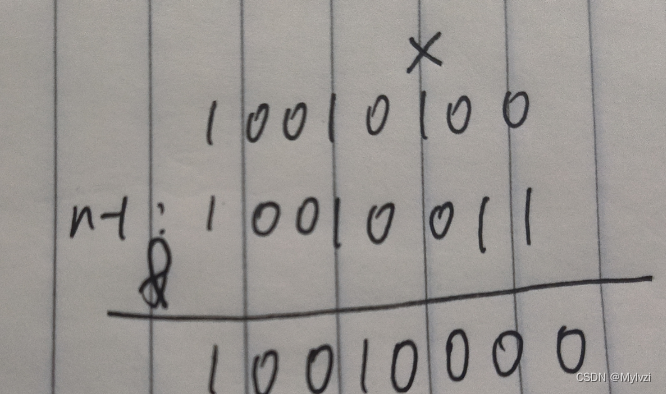
在这里插入图片描述

给定一个数n,将最右侧的1变为0

核心公式:n & (n - 1)
最右侧的1的右边全为0,如果进行 - 1操作,一定会向前要位,直到要位到最右侧的1,最右侧的1变为0,左侧区域不变,右侧区域全部变为1,这就是 n - 1的最终结果

再进行&操作,左侧区域由于相同,最终的结果不变,右侧区域不同,变为0
在这里插入图片描述

3.异或运算规律

a ^ 0 = a
a ^ a = 0
a ^ b ^ c = a ^ (b ^ c)

第三个运算规律非常好用!

二.例题讲解

01.只出现一次的数字
链接:https://leetcode.cn/problems/single-number/description/
分析

  • 经典的位运算问题,使用^操作的运算性质求单身狗问题
  • a^a = 0; a ^ 0 = a
  • 如果数字出现次数为两次,那么^的结果一定是0,最后只会保存只出现一次的那个数字
class Solution {
    public int singleNumber(int[] nums) {
        int x = 0;
        for(int n : nums)
            x ^= n;
        return x;
    }
}

02.只出现一次的数字(III)
链接:https://leetcode.cn/problems/single-number-iii/description/
分析

  • 本题有两个数字出现的次数均为1,将数组中的每一个元素遍历完毕的结果是这两个数字的异或结果,即a^b,想办法将这两个数字分离,找这两个数字的不同点
  • 找ret的lowbit,a和b两个数字在此位置一定是一个为0,一个为1,根据这个性质可以将整个数组分为两类
  • 如何分离?如果nums在lowbit位置为0,则^lowbit的结果一定是0;

在这里插入图片描述
代码:

    public int[] singleNumber(int[] nums) {
        // 1.获得异或结果
        int ret = 0;
        for(int x : nums) {
            ret ^= x;
        }

        // 2.得到最右边的1
        int bitmask = ret & (-ret);

        // 3.分组
        int a = 0, b= 0;
        for(int x : nums) {
            if((x & bitmask) != 0) a ^= x;
            else b ^= x;
        }

        return new int[]{a,b};
    }

03.位1的个数(经典)
链接:https://leetcode.cn/problems/number-of-1-bits/
分析
本题可以看做一个母题了,核心是利用 & 操作统计一个整数的二进制中有多少1

  • n &= (n-1)这个运算是将n的最右侧的1变为0,每运算一次,n的二进制中的1的个数就少1
  • 最终n会变为0,经过几次 n &= (n-1)运算,就有多少个1
    public int hammingWeight(int n) {
        // 本题是经典的统计一个整数的二进制中1的个数问题
        int cnt = 0;
        while(n != 0) {
            n &= (n-1);// 这个操作每次都把n的最右侧的1变为0  一共变了几次就有多少个1
            cnt++;
        }
        return cnt;
    }

相似题:
比特位计数:https://leetcode.cn/problems/counting-bits/

说明:

  • 对于java来说,在Integer包装类内部内置了bitCount方法,专门统计一个整数n的二进制位中1的数目

04.汉明距离(重点)
链接:https://leetcode.cn/problems/hamming-distance/description/
在这里插入图片描述
分析

  • 本题其实是上一题的拓展,在上题中是统计二进制中1的个数,此题也可以进行转化

  • 如果两个数字对应的二进制位不同,只可能是一个为0,一个为1,异或结果一定是1,相同位置异或的结果就是0(设得到的结果为ret)

  • 则ret的二进制中1的数目就是两个数字二进制位不同的位置的数目,这样就转化为求一个整数对应二进制位中1的个数的问题

  • ^操作相同为0,相异为1

代码:

        // 先异或--结果中的1的个数就是x,y中不同的二进制位的个数
        // 转化为判断n中有多少个1
        int n = x ^ y, ret = 0;
        while(n != 0) {
            n &= (n - 1);
            ret ++;
        }
        return ret;

补充:Java中内置了一个求二进制中1的个数的函数

        // Java中内置的统计1的个数的函数
        return Integer.bitCount(x ^ y);

相似题:
汉明距离总和:https://leetcode.cn/problems/total-hamming-distance/

05.判定字符是否唯一(面试题)
链接:https://leetcode.cn/problems/is-unique-lcci/
分析

  • 此题的常规做法很简单,;利用HashMap或/Set来处理重复情况

  • 进阶是不使用任何的数据结构,但是我们需要使用集合来保存字符,在不使用数组的情况下,有一个特别巧妙的方法位图

  • 对于一个整数来说,其本质上是一个32位的二进制数,可以看做是一个长度为32整形数组,数组中只能存储0或1

  • 我们可以使用0和1来作为一种标识,在本题中每遍历到一个字符,就将对应的下标设置为1,代表该字符已经出现,在添加之前先判断该位置是否为1,如果为1,就代表重复出现
    在这里插入图片描述

    public boolean isUnique(String astr) {
        // 位运算解决
        // 使用位图的思想  因为一共只有26中情况(全为小写)
        // 通过这种标记的方式避免使用额外的数据结构
        // 使用一个32位的二进制数
        // 如果字符出现 就将对应的位置标记为1
        int x = 0;
        for(int i = 0; i < astr.length(); i++) {
            char ch = astr.charAt(i);
            int charIndex = ch - 'a';

            // 判断
            if((x & (1 << charIndex)) != 0) return false;
            x |= (1 << charIndex);
        }

        return true;
    }

方法二

  • 还有一种经典的做法使用^1更改奇偶性
  • 尤其是对于二进制压缩问题,数字要么是0,要么是1,假设0代表出现的次数为偶数,1代表出现的次数为奇数
  • 如果原先是0,^1之后成为1,偶数->奇数
  • 如果原先是1,^1之后成为0,奇数->偶数
  • 如果某个字符出现的次数为偶数次,^1的结果一定是0,根据这个条件判断

代码:

class Solution {
    public boolean isUnique(String astr) {
        int x = 0;// 位图数字
        for(char ch : astr.toCharArray()) {
            int charIndex = ch - 'a';// 找到字符对应的位置(下标从0开始)
            x ^= (1 << charIndex);// 异或操作  0->1  1->0
            if((x & (1 << charIndex)) == 0) return false;// 如果有0  证明出现次数为偶数次
        }
        return true;
    }
}

06.消失的两个数字
链接:https://leetcode.cn/problems/missing-two-lcci/description/
分析

  • 本题是只出现一次的数字III和丢失的数字的综合应用

在这里插入图片描述

代码:

class Solution {
    public int[] missingTwo(int[] nums) {
        int n = nums.length;
        int tmp = 0;
        for(int i = 1; i <= n+2; i++) tmp ^= i;

        for(int i = 0; i < n; i++) tmp ^= nums[i];

        // 2.得到最右边的1
        int bitmask = tmp & (-tmp);

        // 3.分组
        int a = 0, b= 0;
        for(int x : nums) {
            if((x & bitmask) != 0) a ^= x;
            else b ^= x;
        }

        for(int i = 1; i <= n + 2; i++) {
            if((i & bitmask) != 0) a ^= i;
            else b ^= i;
        }

        return new int[]{a,b};
    }
}

07.两整数之和
链接:https://leetcode.cn/problems/sum-of-two-integers/
分析

  • 题目要求不能使用+,-等运算符
  • 最经典的做法就是利用^运算的本质是无进位相加的特点
  • ^运算是无进位加法,那么如何产生进位,使其变成正确的结果呢?要进位的地方是两个数字最右边全是1的两个比特位的最近的左边一位,这个位置的计算结果相较于正确结果少了1,需要在这个位置加上1(注意加上之后可能有存在进位,应该重复执行上述操作,直到进位为0)

代码:
循环解法

class Solution {
    public int getSum(int a, int b) {
        while (b != 0) {
            int x = a ^ b;// 无进位加法
            int carry = ((a & b) << 1);// 计算进位
            a = x;
            b = carry;
        }
        return a;
    }
}

递归解法

class Solution {
    public int getSum(int a, int b) {
        if(b == 0) return a;
        return getSum(a ^ b, ((a & b) << 1));
    }
}

09.2的幂
链接:https://leetcode.cn/problems/power-of-two/submissions/542332234/
分析

  • 2的幂的二进制位中,只有一个1

代码
方法一:统计二进制位中1的个数

class Solution {
    public boolean isPowerOfTwo(int n) {
        if(n < 0) return false;
        return Integer.bitCount(n) == 1;
    }
}

方法二:利用n&(n - 1)

  • n&(n-1):将n中最右侧的1更改为0
  • 由于2的幂只有一个1,更改为0之后一定为0
class Solution {
    public boolean isPowerOfTwo(int n) {
        if(n <= 0) return false;
        return ((n & (n - 1)) == 0);
    }
}

10.位运算其他技巧总结
1.不用临时变量交换两个数

int a = 0, b = 0;
a ^= b; // a = a ^ b
b ^= a; // b = b ^ a ^ b = a
a ^= b; // a = a ^ b ^ a = b

2.求绝对值
使用位运算来求整数的绝对值的表达式是 (x ^ (x >> 31)) - (x >> 31)。这是如何工作的：

  1. x >> 31：

    • 这一步将 x 右移31位，如果 x 是一个32位的整数（考虑到符号位），它将填充符号位。对于正数（或0），结果是0；对于负数，结果是-1。
    • 例如，对于 x = -5：
      • 二进制表示： 11111111 11111111 11111111 11111011
      • 右移31位： 11111111 11111111 11111111 11111111（即-1）
      • 对于 x = 5：
      • 二进制表示： 00000000 00000000 00000000 00000101
      • 右移31位： 00000000 00000000 00000000 00000000（即0）

  2. x ^ (x >> 31)：

    • 这一步利用异或运算（XOR）将 x 进行条件取反。如果 x 是负数，它将 x 的每个位进行翻转。如果 x 是正数，这一步不会改变 x。
    • 例如，对于 x = -5：
      • -5 右移31位结果是-1（即所有位都是1）
      • x ^ -1 等于 ~x（即对 x 取反）： 00000000 00000000 00000000 00000100（即4）
      • 对于 x = 5：
      • 5 右移31位结果是0
      • x ^ 0 结果仍然是 5

  3. (x ^ (x >> 31)) - (x >> 31)：

    • 如果 x 是负数，x 取反之后再减去-1，相当于加1，这样就得到了 x 的绝对值。
    • 例如，对于 x = -5：
      • (x ^ -1) 结果是4
      • 再减去-1，结果是5
    • 对于 x = 5：
      • (x ^ 0) 结果是5
      • 再减去0，结果仍然是5

代码实现如下：

public int absolute_value(x) {
    return (x ^ (x >> 31)) - (x >> 31);
}

3.判断两个数符号是否相同
使用位运算判断两个数的符号是否相同可以通过 (a ^ b) >= 0 来实现。以下是原理解释：

  1. a ^ b：

    • 异或运算 a ^ b 会比较 a 和 b 的每一个对应的二进制位，如果相同则结果为0，不同则结果为1。
    • 对于符号位（最高位），如果 a 和 b 的符号相同（即符号位相同），则 a ^ b 的符号位将是0；如果符号不同，符号位将是1。
    • 因此，如果 a 和 b 符号相同，结果是非负数（符号位为0）；如果符号不同，结果是负数（符号位为1）。

  2. (a ^ b) >= 0：

    • 通过检查 a ^ b 是否为非负数，可以判断 a 和 b 的符号是否相同。如果 a ^ b 的结果大于等于0，说明符号相同；否则符号不同。

代码实现如下：

public boolean have_same_sign(a, b){
    return (a ^ b) >= 0;
}

总结:

  1. 对于位运算这个算法,预期叫做一种思想,不如当做一种技巧,是一个加快运算速度的技巧
  2. 记住常见的集中位运算的性质和经典题目就可(求二进制中1的个数.利用^操作更改奇偶性,利用&1操作判断元素的奇偶性…)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1868380.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

昇思25天学习打卡营第4天|linchenfengxue

昇思25天学习打卡营第4天|linchenfengxue

需求&#xff1a;建立一个图像分类模型&#xff0c;提供自动识别有(猫、狗、飞机、汽车等等) 图片的功能 ResNet50图像分类 图像分类是最基础的计算机视觉应用&#xff0c;属于有监督学习类别&#xff0c;如给定一张图像(猫、狗、飞机、汽车等等)&#xff0c;判断图像所属的类…
阅读更多...
【直播倒计时】面向AI领域的开发工程师：TinyML在国产FPGA的边缘AI加速应用

【直播倒计时】面向AI领域的开发工程师：TinyML在国产FPGA的边缘AI加速应用

TinyML是机器学习中的一个新兴领域&#xff0c;专注于开发可在低功耗、内存受限的设备上运行的算法和模型。其核心目标是将先进的机器学习算法和模型移植到体积小巧、能耗极低的嵌入式设备中&#xff0c;使这些设备具备边缘智能&#xff0c;能够在没有外部服务器支持的情况下进…
阅读更多...
05 threeJs基础---阵列立方体和相机适配体验立方体

05 threeJs基础---阵列立方体和相机适配体验立方体

1.增加相机视角fov 注&#xff1a; 范围更大&#xff0c;意味着可以看到渲染范围更大&#xff0c;远小近大的视觉效果更明显 fov:眼球张开的角度&#xff0c;0时相当于闭眼。aspect:可视区域横纵比。near:眼睛能看到的最近垂直距离。far&#xff1a;眼睛能看到的最远垂直距离。…
阅读更多...
Python类的定义和管理库之attrs使用详解

Python类的定义和管理库之attrs使用详解

概要 在 Python 编程中，定义类和数据结构是常见的任务。然而，手动编写类的初始化方法、属性验证和比较方法可能会非常繁琐和容易出错。attrs 库是一个功能强大且灵活的工具，旨在简化类的定义和管理。通过使用 attrs，开发者可以轻松定义不可变对象、进行属性验证和类型检查…
阅读更多...
2024长三角快递物流展即将开幕点击收藏逛展不迷路~

2024长三角快递物流展即将开幕点击收藏逛展不迷路~

2024长三角快递物流展是亚洲范围内超大规模的快递物流业展示平台&#xff0c;由于展会的需求及扩大市场的影响力&#xff0c;ESYE2004转战杭州&#xff0c;凭借着先进的经济发展水平、优越的地理位置、成熟的产业环境以及巨大的电商、微商、零售业、消费的市场空间&#xff0c;…
阅读更多...
SAP标准报表 S_ALR_8701XXXX是没有export to excel的 或者禁用 %PC也禁用了，如何开回来

SAP标准报表 S_ALR_8701XXXX是没有export to excel的 或者禁用 %PC也禁用了，如何开回来

以 s_alr_87012172为例子 系统-状态 进入程序 搜索 XXL 做下替换
阅读更多...
大型企业组网如何规划网络

大型企业组网如何规划网络

大型企业组网是一个复杂的过程&#xff0c;它需要细致的规划和设计&#xff0c;以确保网络能够满足企业的业务需求&#xff0c;同时保证性能、安全性和可扩展性。以下是规划大型企业网络的一些关键步骤和考虑因素&#xff1a; 1. 需求分析 业务需求&#xff1a;与各个业务部门…
阅读更多...
如何使用WordPress进行外贸建站？

如何使用WordPress进行外贸建站？

使用 进行外贸建站既简单又高效&#xff0c;搭建一个外贸网站是一个绝佳的方式来展示你的产品和服务&#xff0c;吸引全球客户&#xff0c;wordpress本身是一个高度可定制化的建站程序&#xff0c;只要你想&#xff0c;他能变成购物网站&#xff0c;宣传网站&#xff0c;所以第…
阅读更多...
Centos安装Snaped

Centos安装Snaped

本人操作系统为Centos 7 1. 安装epel 和 copr yum #第一步安装epel sudo yum install epel-release #第二步安装copr sudo yum install yum-plugin-copr 2. 添加存储库 sudo yum copr enable ngompa/snapcore-el7 3. 安装snapd软件包 sudo yum -y install snapd 等待安装完…
阅读更多...
window10/11如何下载安装JDK(jdk) 超详细图文教程

window10/11如何下载安装JDK(jdk) 超详细图文教程

1、下载jdk 下载安装jdk17&#xff0c;网盘点此下载&#xff1a;https://pan.quark.cn/s/1fb394c360f0 也可以去官网下载&#xff0c;选择如图所示的版本&#xff0c;点击下载。 2、开始安装 双击下载好的exe进行安装 全程点击下一步即可&#xff0c;只有安装路径需要修改以…
阅读更多...
基于STM32+华为云IOT设计的智能冰箱(华为云IOT)

基于STM32+华为云IOT设计的智能冰箱(华为云IOT)

文章目录 一、前言1.1 项目介绍【1】项目开发背景【2】设计实现的功能【3】项目硬件模块组成【4】摘要 1.2 设计思路1.3 系统功能总结1.4 开发工具的选择【1】设备端开发【2】上位机开发 二、部署华为云物联网平台2.1 物联网平台介绍2.2 开通物联网服务2.3 创建产品&#xff08…
阅读更多...
TypeError: %c requires int or char

TypeError: %c requires int or char

踩坑&#xff1a;在用python写脚本查询sql数据时&#xff0c;使用%s来替换sql语句里的变量&#xff0c;结果一直报&#xff0c;而其他sql使用同样的方法正常&#xff0c;最后发现是因为sql语句里有模糊查询 like "%测试%"&#xff0c;这里的%被误以为%s&#xff0c;解…
阅读更多...
昇思25天学习打卡营第9天|基于 MindSpore 实现 BERT 对话情绪识别

昇思25天学习打卡营第9天|基于 MindSpore 实现 BERT 对话情绪识别

学AI还能赢奖品&#xff1f;每天30分钟&#xff0c;25天打通AI任督二脉 (qq.com) 环境配置 %%capture captured_output # 实验环境已经预装了mindspore2.2.14&#xff0c;如需更换mindspore版本&#xff0c;可更改下面mindspore的版本号 !pip uninstall mindspore -y !pip in…
阅读更多...
valgrind调试c/c++内存问题:非法地址访问_内存泄漏_越界访问

valgrind调试c/c++内存问题:非法地址访问_内存泄漏_越界访问

1.valgrind命令 调试内存问题: valgrind --leak-checkfull 更新详细的显示: valgrind --leak-checkfull --show-leak-kindsall valgrind提示信息汇总 内存泄漏 lost in loss record 丢失记录 , 内存泄漏实例[[#2.内存泄漏–不完全释放内存|实例链接]]段错误 Process termina…
阅读更多...
如何解决Oracle中PL Developer过期

如何解决Oracle中PL Developer过期

如果长时间不使用PL Deveploer&#xff0c;再次打开有可能会出现以下页面&#xff1a; 上方页面说明此软件已经过期&#xff0c;有两种方法可以解决上述问题&#xff0c;第一种&#xff1a; 操作注册表&#xff1a; WinR 输入指令“regedit”打开注册表&#xff0c;出现下方页…
阅读更多...
Camera开发-相机输出常用数据格式

Camera开发-相机输出常用数据格式

作者简介&#xff1a; 一个平凡而乐于分享的小比特&#xff0c;中南民族大学通信工程专业研究生在读&#xff0c;研究方向无线联邦学习 擅长领域&#xff1a;驱动开发&#xff0c;嵌入式软件开发&#xff0c;BSP开发 作者主页&#xff1a;一个平凡而乐于分享的小比特的个人主页…
阅读更多...
STM32HAL库--定时器篇(速记版)

STM32HAL库--定时器篇(速记版)

STM32F429 有14个定时器&#xff0c;其中包括 2 个基本定时器&#xff08;TIM6 和 TIM7&#xff09;、 10 个通用定时器&#xff08;TIM2~TIM5&#xff0c;TIM9~TIM14&#xff09;、 2 个高级控制定时器&#xff08;TIM1 和 TIM8&#xff09;。 由上表知道&#xff1a;除了 TIM…
阅读更多...
具备生成自签名文档证书能力的印章管理软件_电子骑缝章软件

具备生成自签名文档证书能力的印章管理软件_电子骑缝章软件

最新版的e-章宝具体生成自签名文档证书的能力&#xff0c;这种证书可用内部文档发布的签名&#xff0c;文档一旦用证书签名并发布&#xff0c;具有不可抵赖性&#xff0c;阅读者也能确认所发布的文档是否是发布者发布的&#xff08;即中途有没有被他人恶意修改过&#xff09;&a…
阅读更多...
成熟ICT测试系统与LabVIEW定制开发的比较

成熟ICT测试系统与LabVIEW定制开发的比较

ICT&#xff08;In-Circuit Test&#xff09;测试系统是电子制造行业中用于电路板&#xff08;PCB&#xff09;组件检测的重要工具。市场上有许多成熟的ICT测试系统&#xff0c;如Keysight、Teradyne、SPEA等公司提供的商用解决方案。此外&#xff0c;LabVIEW作为一种强大的图形…
阅读更多...
如何在ArcGIS Pro中提取行政区划

如何在ArcGIS Pro中提取行政区划

我们在《2024版有审图号的SHP行政区划》一文中&#xff0c;为你分享过全国省市县级的行政区划。 现在再为你分享一下&#xff0c;如何在ArcGIS Pro中提取目标范围行政区划的方法&#xff0c;你还可在以文末查看领取该行政区划数据的方法。 直接选择 在菜单栏上点击一下选择下…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023