对于线性模型来说，想要丰富特征，还有一种方法是添加原始数据的交互特征和多项式特征。这种特征工程通常用于统计建模，但也经常用于实际的机器学习应用中。

交互特征

上一篇的例子里，线性模型对wave数据集的的每个箱子都学到一个常数值，但线性模型不仅可以学习偏移，还可以学习斜率。想要向分箱数据上的线性模型添加斜率，一种方法是重新假如原始特征，这样就会得到11维的数据：

from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import OneHotEncoder

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

X,y=mglearn.datasets.make_wave(n_samples=100)
line=np.linspace(-3,3,1000,endpoint=False).reshape(-1,1)
bins=np.linspace(-3,3,11)
which_bin=np.digitize(X,bins=bins)
#使用OneHotEncoder进行变换
encoder=OneHotEncoder(sparse=False)
encoder.fit(which_bin)
#transform创建one-hot编码
X_binned=encoder.transform(which_bin)
line_binned=encoder.transform(np.digitize(line,bins=bins))
X_combined=np.hstack([X,X_binned])
print(X_combined.shape)

reg=LinearRegression().fit(X_combined,y)

line_combined=np.hstack([line,line_binned])
plt.plot(line,reg.predict(line_combined),label='线性回归()')

for bin in bins:
    plt.plot([bin,bin],[-3,3],':',c='k')

plt.legend(loc='best')
plt.xlabel('输入特征')
plt.ylabel('回归 输出')
plt.plot(X[:,0],y,'o',c='k')

plt.show()

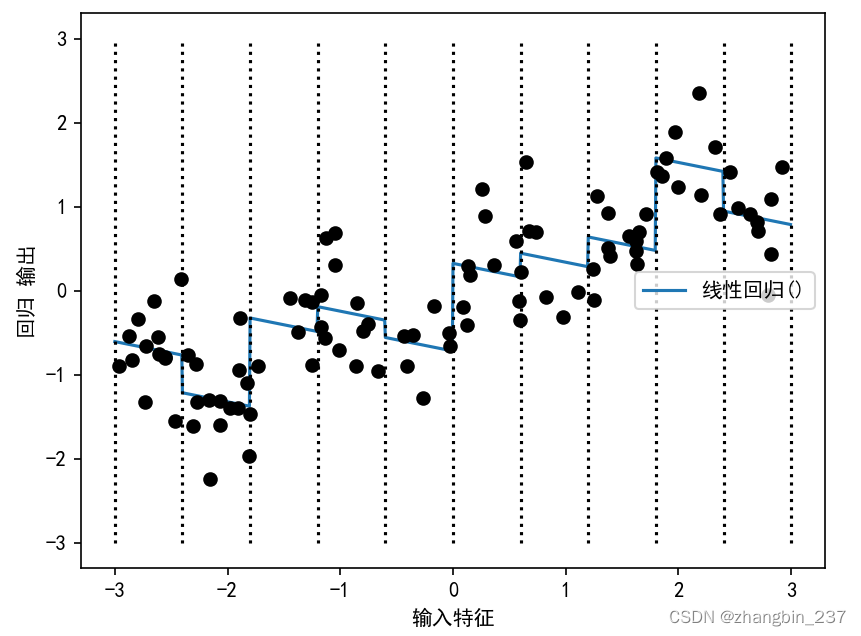
在这个例子中，模型在每个箱子都学到一个偏移，还学到一个斜率。学到的斜率是向下的，而且每个箱子都相同，也就是只有一个x轴特征，只有一个斜率。因为斜率在所有箱子都是相同的，所以它似乎不是很有用，我们更希望每个箱子都有一个不同的斜率。

为了实现这一点，我们可以添加交互特征或乘积特征，用来表示数据点所在的箱子以及数据点在x轴的位置。这个特征就是箱子指示符与原始特征的乘积。创建数据集：

X_product=np.hstack([X_binned,X*X_binned])
print(X_product.shape)

这个数据集现在有20个特征：数据点所在箱子的指示符与原始特征和箱子指示符的乘积。

我们可以将乘积特征看作每个箱子x轴特征的单独副本。它在箱子内等于原始特征，在其位置等于0：

reg=LinearRegression().fit(X_product,y)
line_combined=np.hstack([line_binned,line*line_binned])
plt.plot(line,reg.predict(line_combined),label='线性回归()')

for bin in bins:
    plt.plot([bin,bin],[-3,3],':',c='k')

plt.legend(loc='best')
plt.xlabel('输入特征')
plt.ylabel('回归 输出')
plt.plot(X[:,0],y,'o',c='k')

plt.show()

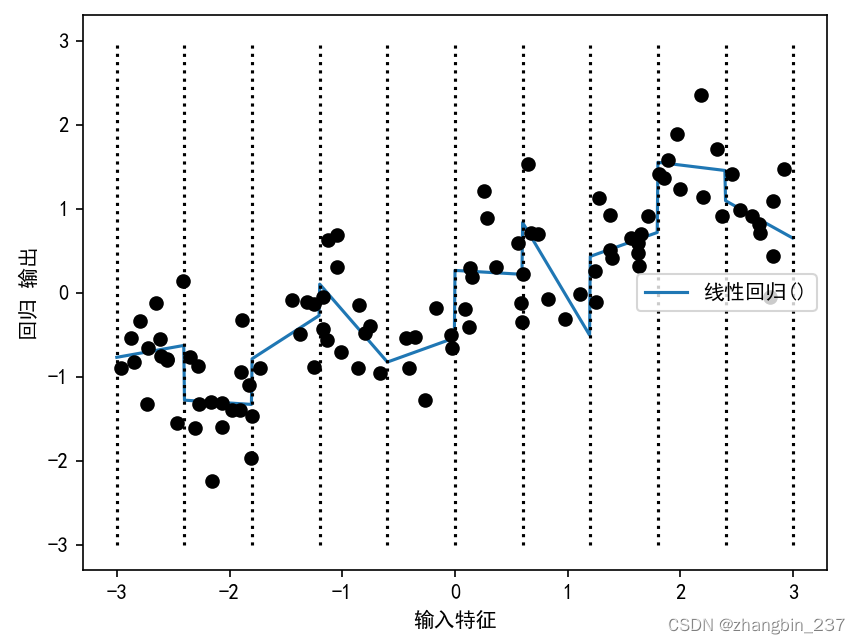
可以看到，现在这个模型中，每个箱子都有自己的偏移和斜率。

多项式特征

使用分箱是扩展连续特征的一种方法。另一种方法是使用原始特征的多项式。对于给定特征x，我们可以考虑x**2、x**3、x**4等等，这在preprocessing模块的PolynomialFeatures中实现：

from sklearn.preprocessing import PolynomialFeatures


#包含直到x**10的多项式
ploy=PolynomialFeatures(degree=10,include_bias=False)
ploy.fit(X)
X_ploy=ploy.transform(X)
print(X_ploy.shape)

多项式的次数为10，因此生成了10个特征。

我们比较X_ploy和X的元素：

print('Entries of X:\n{}'.format(X[:5]))
print('Entries of X_ploy:\n{}'.format(X_ploy[:5]))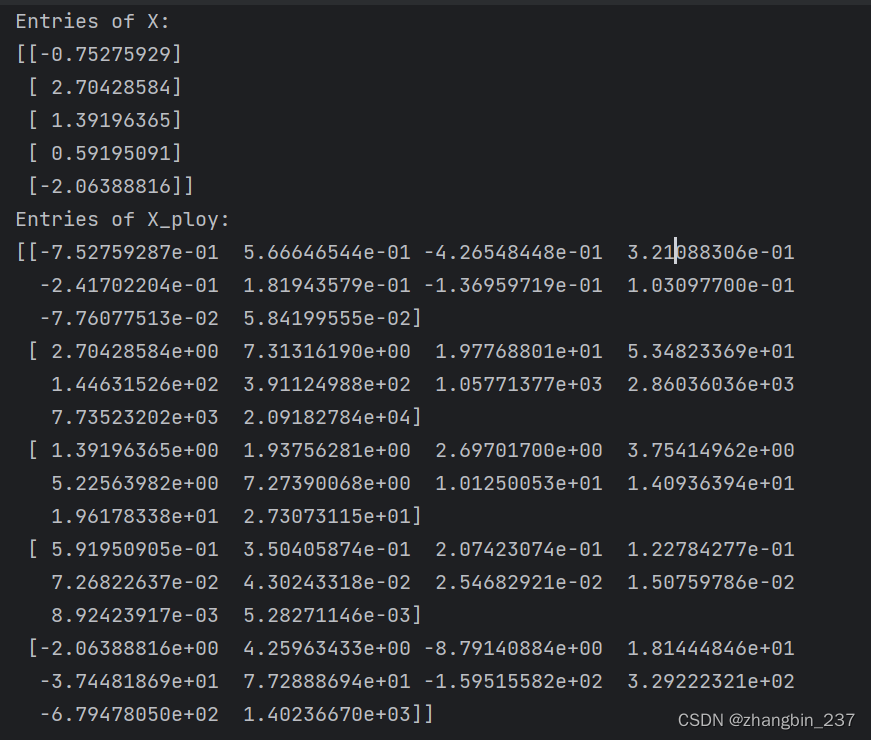

我们还可以通过调用get_feature_names_out方法来获取特征的语义，来给出每个特征的指数：

print('Polynomial feature names:{}'.format(ploy.get_feature_names_out()))

可以看到，X_ploy的第一列与X完全对应，而其他列则是第一列的幂。

将多项式特征与线性回归模型一起使用，可以得到经典的多项式回归模型：

reg=LinearRegression().fit(X_ploy,y)
line_ploy=ploy.transform(line)
plt.plot(line,reg.predict(line_ploy),label='线性回归(多项式回归)')

plt.plot(X[:,0],y,'o',c='k')
plt.legend(loc='best')
plt.xlabel('输入特征')
plt.ylabel('回归 输出')

plt.show()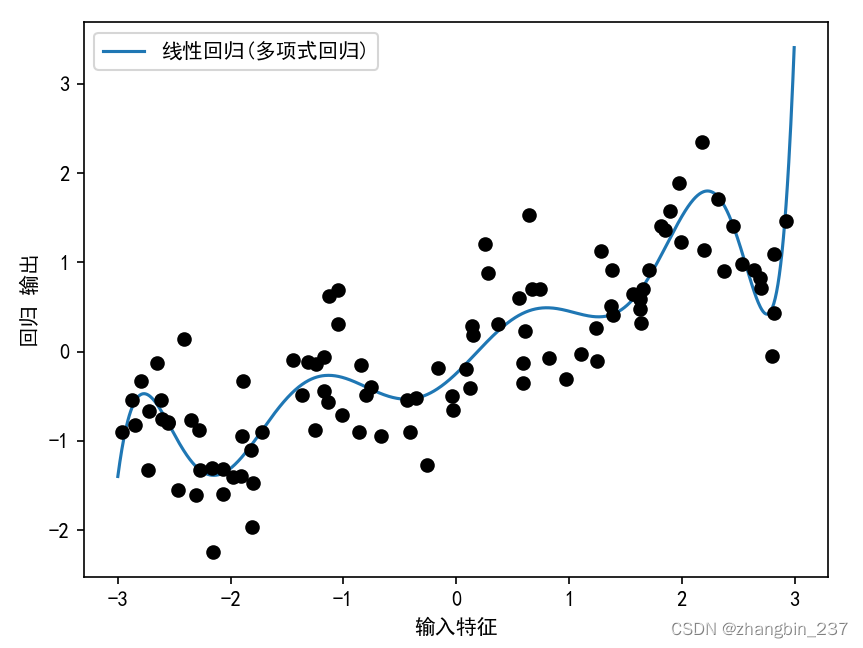

可以看到，多项式特征在这个一维数据上得到了非常平滑的拟合，但高次多项式在边界或数据很少的区域可能会有极端的表现。

作为对比，下面是原始数据上学到的核SVM模型，没有做任何变换：

from sklearn.svm import SVR

for gamma in [1,10]:
    svr=SVR(gamma=gamma).fit(X,y)
    plt.plot(line,svr.predict(line),label='SVR gamma={}'.format(gamma))


plt.plot(X[:,0],y,'o',c='k')
plt.legend(loc='best')
plt.xlabel('输入特征')
plt.ylabel('回归 输出')

plt.show()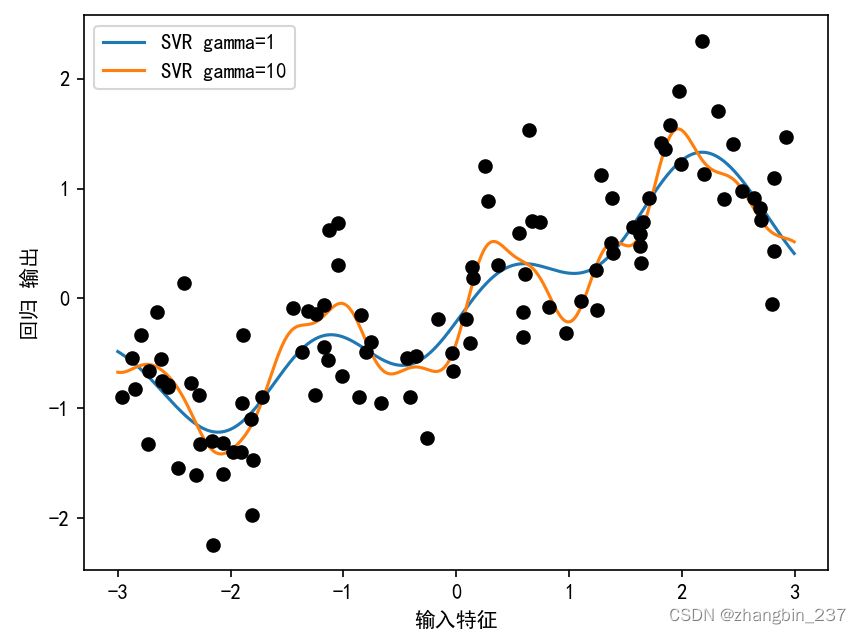

使用更复杂的模型（也就是核SVM），我们能够学习到一个与多项式回归的复杂度类似的预测结果，且不需要进行显式的特征变换。