【深度学习】基于深度离散潜在变量模型的变分推理

1.引言

1.1.讨论的目标

阅读并理解本文后，大家应能够：

掌握如何为具有离散潜在变量的模型设定参数
在可行的情况下，使用精确的对数似然函数来估计参数
利用神经变分推断方法来估计参数

1.2.导入相关软件包

# 导入PyTorch库，用于深度学习相关的操作。
import torch
# 导入NumPy库，用于进行科学计算。
import numpy as np
# 导入Python的random库，用于设置随机数生成器的种子。
import random
# 导入matplotlib.pyplot，用于绘图。
import matplotlib.pyplot as plt
# 导入PyTorch的神经网络模块。
import torch.nn as nn
# 导入PyTorch的函数库，用于一些常用的操作，如激活函数。
import torch.nn.functional as F
# 导入PyTorch的分布库，用于处理概率分布。
import torch.distributions as td

# 从itertools库导入chain函数，用于迭代多个可迭代对象。
from itertools import chain
# 从collections库导入defaultdict和OrderedDict，用于创建特殊类型的字典。
from collections import defaultdict, OrderedDict
# 从tqdm.auto导入tqdm，用于显示进度条。
from tqdm.auto import tqdm

# 从IPython.display导入set_matplotlib_formats，用于设置matplotlib的图形格式。
from IPython.display import set_matplotlib_formats
# 设置matplotlib图形的格式为SVG和PDF，SVG格式适合网页显示，PDF格式适合打印。
set_matplotlib_formats('svg', 'pdf') 
# 导入matplotlib配置，用于设置图形的全局参数。
import matplotlib
# 设置matplotlib图形的线宽。
matplotlib.rcParams['lines.linewidth'] = 2.0

# 确保matplotlib图形在Jupyter Notebook中以inline方式显示。
%matplotlib inline

# 定义一个函数seed_all，用于设置所有随机数生成器的种子，以确保实验的可复现性。
def seed_all(seed=42):
    # 设置NumPy的随机种子。
    np.random.seed(seed)
    # 设置Python内置random模块的种子。
    random.seed(seed)
    # 设置PyTorch的随机种子。
    torch.manual_seed(seed)

# 调用seed_all函数，设置默认的随机种子。
seed_all()

1.3.数据准备

为了本文的实验验证，我们将使用玩具图像数据集(FashionMNIST)。这些数据集包含固定维度的观测值，因此设计编码器和解码器相对简单。通过这种方式，我们可以将注意力集中在概率性质的核心部分。

# 从torchvision.datasets导入FashionMNIST数据集。
from torchvision.datasets import FashionMNIST
# 导入torchvision的transforms模块，用于数据预处理。
from torchvision import transforms
# 导入ToTensor转换，用于将PIL图像或Numpy数组转换为`FloatTensor`。
from torchvision.transforms import ToTensor
# 从torch.utils.data导入random_split和Dataset，用于数据集的划分和创建。
from torch.utils.data import random_split, Dataset
# 从torch.utils.data.dataloader导入DataLoader，用于创建数据加载器。
from torch.utils.data.dataloader import DataLoader
# 从torchvision.utils导入make_grid，用于将图像集合排列成一个网格。
from torchvision.utils import make_grid
# 导入PyTorch的优化器模块。
import torch.optim as opt

# 设置数据集的路径。
DATASET_PATH = "../../data"
# 根据是否有可用的GPU，设置运行设备。
my_device = torch.device("cuda:0") if torch.cuda.is_available() else torch.device("cpu")

# 定义一个二值化转换的Dataset类。
class Binarizer(Dataset):
    def __init__(self, ds, threshold=0.5):
        self._ds = ds  # 原始数据集
        self._threshold = threshold  # 二值化的阈值

    def __len__(self):
        # 返回数据集的大小。
        return len(self._ds)

    def __getitem__(self, idx):
        # 根据索引idx获取数据，并进行二值化处理。
        x, y = self._ds[idx]
        return (x >= self._threshold).float(), y

# 加载FashionMNIST数据集，并应用数据增强变换。
dataset = FashionMNIST(root=DATASET_PATH, train=True, download=True,
               transform=transforms.Compose([transforms.Resize(64), transforms.ToTensor()]))
# 打印出第一张图片的形状。
img_shape = dataset[0][0].shape
print("Shape of an image:", img_shape)

# 设置验证集的大小。
val_size = 1000
# 计算训练集的大小。
train_size = len(dataset) - val_size
# 划分训练集和验证集。
train_ds, val_ds = random_split(dataset, [train_size, val_size])

# 打印训练集和验证集的大小。
print(len(train_ds), len(val_ds))

# 设置是否将数据二值化的标志。
bin_data = True
if bin_data:
    # 如果需要，将训练集和验证集转换为二值化数据集。
    train_ds = Binarizer(train_ds)
    val_ds = Binarizer(val_ds)

# 设置批大小。
batch_size = 64
# 创建训练集的数据加载器。
train_loader = DataLoader(train_ds, batch_size, shuffle=True, num_workers=2, pin_memory=True)
# 创建验证集的数据加载器。
val_loader = DataLoader(val_ds, batch_size, num_workers=2, pin_memory=True)

# 遍历训练集的迭代器。
for images, y in train_loader:
    # 打印一批图像的形状。
    print('images.shape:', images.shape)
    # 创建一个图形，不显示坐标轴。
    plt.figure(figsize=(16,8))
    plt.axis('off')
    # 将图像集合排列成一个网格并显示。
    plt.imshow(make_grid(images, nrow=16).permute((1, 2, 0)))
    plt.show()
    # 展示一张图像后退出循环。
    break

2. 潜在变量模型

在本节中，我们将利用神经网络来定义一个涉及潜在变量的模型，也就是对一组随机变量的联合概率分布进行建模，其中部分变量可以被观察到，而另一部分则不能。

我们特别关注以下两种随机变量：

一个离散的潜在代码 $\in \mathcal{Z}$
一张图像 $\in \mathcal{X}$ ，它是实数空间 $\mathbb{R}^D$ 的一个子集

图像 $x$ 由 $C$ 个颜色通道、宽度 $W$ 和高度 $H$ 定义，因此 $\mathcal{X}$ 属于 $\mathbb{R}^{C \times W \times H}$ 。由于我们设定了 $\times W \times H$ ， $\mathcal{X}$ 是具有有限维度的，但这不是必须的（例如，在其他领域中， $\mathcal{X}$ 可能是无限的，包含任意长度的所有句子）。我们可以将像素强度视为离散或连续变量，前提是我们为每种情况选择了恰当的概率质量函数或概率密度函数。

我们将探讨两种潜在代码类型：一种是分类代码 $\in \{1, \ldots, K\}$ ，另一种是组合代码 $\in \{0, 1\}^K$ 。在这两种情况下， $\mathcal{Z}$ 都是可数的，但这不是必须的（例如， $z$ 可以是自然数或任意长度的潜在序列）。

我们通过定义一个联合概率密度函数来指定 $\mathcal{Z}$ 和 $\mathcal{X}$ 上的联合分布：

$p_{ZX}(z, x|\theta) = p_Z(z|\theta) \times p_{X|Z}(x|z, \theta)$

这里的 $\theta$ 表示神经网络的参数，这些网络参数化了概率质量函数 $p_Z$ 和对于任何给定 $z$ 的条件概率密度函数 $p_{X|Z=z}$ 。

本文中的先验分布是固定的，但在其他情况下可能并非如此。我们没有其他预测变量作为条件，但在某些应用场景中可能会有（例如，在图像描述任务中，我们可能对给定图像 $x$ 的标题 $y$ 和潜在代码 $z$ 的联合分布感兴趣；在图像生成任务中，我们可能对给定标题 $y$ 的图像 $x$ 和潜在代码 $z$ 的联合分布感兴趣）。

2.1 先验网络

我们的讨论首先从定义和描述一个组件开始，这个组件用于参数化先验分布 $p_Z$ 。

先验网络是一种神经网络，其主要功能是为一批数据实例提供一个固定的先验分布的参数化表达。

class PriorNet(nn.Module):  
    """  
    先验网络：用于参数化先验分布的神经网络。  
  
    在本实验中，我们的先验是固定的，因此该神经网络的前向传播  
    只是返回一个具有给定batch_shape的固定先验。  
    """  
  
    def __init__(self, outcome_shape: tuple):  
        """  
        outcome_shape: 单个结果的形状。  
        如果你使用一个整数k，我们将会把它转换为(k,)的元组形式。  
        """  
        super().__init__()  
        if isinstance(outcome_shape, int):  
            # 如果outcome_shape是整数，则转换为元组形式  
            outcome_shape = (outcome_shape,)  
        self.outcome_shape = outcome_shape  
  
    def forward(self, batch_shape):  
        """  
        返回批次对应的先验分布对象。  
  
        Args:  
            batch_shape (tuple): 批次的形状。  
  
        Returns:  
            td object: 表示先验分布的torch.distributions对象（待实现）。  
  
        Raises:  
            NotImplementedError: 因为这个函数需要被实现。  
        """  
        raise NotImplementedError("需要实现此函数以返回先验分布对象！")  
  
# 注意：在实际实现中，您可能需要使用torch.distributions中的某个分布类来创建先验分布对象。  
# 例如，如果您想要一个正态分布的先验，您可以使用torch.distributions.Normal。

伯努利分布的乘积先验

当我们的潜在编码是一个 $K$ 维的比特向量时，每个比特都可以视为数据点的一个属性。对于这样的编码，我们为每一个坐标使用均匀分布的伯努利先验：

$p_Z(z) = \prod_{k=1}^K \text{Bernoulli}(z_k|0.5)$

这意味着每个比特都有0.5的概率是1，0.5的概率是0。

均匀独热类别先验

若潜在编码是从一个离散集合 $\{1, \ldots, K\}$ 中选取的一个类别，我们可以为该类别使用均匀的先验分布：

$p_Z(z) = \text{Categorical}(z|K^{-1} \mathbf{1}_K)$

其中， $\mathbf{1}_K$ 是一个 $K$ 维的全1向量。这个先验确保每个类别被选中的概率都是相等的，即 $1/ K$ 。

在实际应用中，我们可以使用“OneHotCategorical”分布来简化操作，它会自动将类别分布的样本转换为独热编码形式。

class BernoulliPriorNet(PriorNet):
    """伯努利先验网络，用于D维位向量z：
        p(z) = ∏ p(z[d] | 0.5)，其中p是伯努利分布。
    """
    
    def __init__(self, outcome_shape):
        super().__init__(outcome_shape)  # 调用基类的构造函数
        # 注册一个不需要梯度的缓冲区logits，初始化为0
        self.register_buffer("logits", torch.zeros(self.outcome_shape, requires_grad=False).detach())

    def forward(self, batch_shape):
        # 计算分布的形状
        shape = batch_shape + self.outcome_shape
        # 使用td.Independent来获得多变量抽样的概率质量函数（pmf）
        # 如果没有td.Independent，我们将得到多个pmf而不是一个多变量结果空间的pmf
        # td.Independent将最右边的维度解释为结果形状的一部分
        return td.Independent(td.Bernoulli(logits=self.logits.expand(shape)), len(self.outcome_shape))

class CategoricalPriorNet(PriorNet):
    """分类先验网络，用于z是K个类别集合中一个类别的一位有效编码：
        p(z) = OneHotCategorical(z | torch.ones(K) / K)
    """
    
    def __init__(self, outcome_shape):
        super().__init__(outcome_shape)  # 调用基类的构造函数
        self.register_buffer("logits", torch.zeros(self.outcome_shape, requires_grad=False).detach())

    def forward(self, batch_shape):
        shape = batch_shape + self.outcome_shape
        # OneHotCategorical是对Categorical的包装，
        # 在抽取Categorical样本后，td.OneHotCategorical使用onehot(sample, support_size)对其进行编码
        # 在这里我们不需要td.Independent，因为OneHotCategorical是对多变量抽样的概率分布
        # 这与伯努利先验的乘积不同
        return td.OneHotCategorical(logits=self.logits.expand(shape))

# 测试先验网络的函数
def test_priors(batch_size=3):
    prior_net = BernoulliPriorNet(7)
    print("\n伯努利先验")
    print(f" outcome_shape={prior_net.outcome_shape}")
    p = prior_net(batch_shape=(batch_size,))
    print(f" 分布: {p}")
    z = p.sample()  # 抽取一个样本
    print(f" 样本: {z}")
    print(f" 形状: sample={z.shape} log_prob={p.log_prob(z).shape}")

    prior_net = CategoricalPriorNet(7)
    print("\n分类先验")
    print(f" outcome_shape={prior_net.outcome_shape}")
    p = prior_net(batch_shape=(batch_size,))
    print(f" 分布: {p}")
    z = p.sample()
    print(f" 样本: {z}")
    print(f" 形状: sample={z.shape} log_prob={p.log_prob(z).shape}")

# 调用测试函数
test_priors()

伯努利先验
 outcome_shape=(7,)
分布: Independent(Bernoulli(logits: torch.Size([3, 7])), 1)
样本: tensor([[0., 0., 0., 1., 1., 1., 0.],
        [1., 0., 1., 0., 1., 0., 0.],
        [1., 0., 0., 1., 1., 1., 1.]])
形状: sample=torch.Size([3, 7]) log_prob=torch.Size([3])

分类先验
 outcome_shape=(7,)
分布: OneHotCategorical()
样本: tensor([[0., 0., 1., 0., 0., 0., 0.],
        [1., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 1., 0., 0.]])
形状: sample=torch.Size([3, 7]) log_prob=torch.Size([3])

2.2 条件概率分布

本节我们将通过神经网络来参数化条件概率分布（CPDs），具体做法是让神经网络学习并输出某个概率质量函数（PMF）或概率密度函数（PDF）的参数。这一步骤对于构建潜在变量模型中的 $p_{X|Z=z}$ 组件至关重要（并且，在后续的发展中，它也将对变分推断中的 $q_{Z|X=x}$ 组件有所帮助）。

我们的基本策略是，根据用户选择的输入，通过神经网络映射到由torch.distributions库支持的PMF或PDF的参数上。

class CPDNet(nn.Module):  
    """  
    CPDNet类：一个用于参数化条件概率分布的神经网络。  
  
    假设L是某个选定的分布，x ~ L 是具有outcome_shape形状的一个结果。  
  
    CPDNet的前向传播方法将多个输入映射到L的pmf/pdf的参数上，  
    并返回一个表示L的pmf/pdf的torch.distributions对象。  
    """  
  
    def __init__(self, outcome_shape):  
        """  
        初始化方法。  
  
        outcome_shape: 单个结果的形状。  
        如果传入一个整数k，则将其转换为元组形式(k,)。  
        """  
        super().__init__()  # 调用父类nn.Module的初始化方法  
        if isinstance(outcome_shape, int):  
            # 如果outcome_shape是整数，则转换为元组形式  
            outcome_shape = (outcome_shape,)  
        self.outcome_shape = outcome_shape  
  
    def forward(self, inputs):  
        """  
        前向传播方法。  
  
        根据输入`inputs`预测并返回一个torch.distributions对象。  
  
        inputs: 形状为batch_shape + (num_inputs,)的张量，  
                其中batch_shape是批次形状，num_inputs是输入特征的数量。  
  
        返回: 一个torch.distributions对象，表示根据输入预测的条件概率分布。  
  
        注意: 该方法需要被子类重写以实现具体的条件概率分布参数化逻辑。  
        """  
        raise NotImplementedError("请在此处实现具体的前向传播逻辑")  
  
# 注意：在实际使用中，子类应该实现forward方法以完成具体的条件概率分布参数化。

2.2.1 观测模型

观测模型定义了给定隐变量 $Z = z$ 时，观测变量 $X$ 的分布。

如果像素强度是二值化的，我们可以使用 $\times W \times H$ 个伯努利分布的乘积来表示这个分布，并通过一个神经网络来联合参数化这些分布。具体来说，我们有：

$p_{X|Z}(x|z, \theta) = \prod_{c=1}^{C}\prod_{w=1}^{W}\prod_{h=1}^{H} \mathrm{Bernoulli}(x_{c,w,h} | f_{c,w,h}(z; \theta))$

其中， $f_{c,w,h}(z; \theta)$ 是神经网络 $\mathbf{f}(z; \theta)$ 的输出，表示在给定 $z$ 和参数 $\theta$ 时，位置 $(c, w, h)$ 处像素强度为1的概率。这里， $\mathbf{f}(z; \theta)$ 是一个神经网络架构，如全连接网络或转置卷积层的堆叠，通常被称为解码器。

如果像素强度是 $[0, 1]$ 范围内的实数，我们需要选择一个合适的概率密度函数（pdf）来参数化分布。在这种情况下，一个合适的选择是连续伯努利分布，它是一个单参数分布，其支撑集是 $[0, 1]$ ，与伯努利分布类似。

接下来，我们将设计这个神经网络 $\mathbf{f}$ 。

class ReshapeLast(nn.Module):  
    """  
    辅助层，用于重塑张量的最右侧维度。  
  
    可以作为 nn.Sequential 的一部分使用。  
    """  
  
    def __init__(self, shape: tuple):  
        """  
        shape: 所需的最右侧维度形状  
        """  
        super().__init__()  
        self._shape = shape  
  
    def forward(self, input):  
        # 将最后一个维度重塑为 self.shape  
        return input.reshape(input.shape[:-1] + self._shape)  
  
  
def build_ffnn_decoder(latent_size, num_channels, width=64, height=64, hidden_size=512, p_drop=0.):  
    """  
    使用具有2个隐藏层的全连接神经网络（FFNN）将潜在编码映射到形状为 [num_channels, width, height] 的张量。  
  
    latent_size: 潜在编码的大小  
    num_channels: 输出中的通道数  
    width: 图像宽度  
    height: 图像高度  
    hidden_size: 我们首先将 latent_size 映射到 hidden_size，然后使用前馈神经网络将其映射到 [num_channels, width, height]  
    p_drop: 线性层之前的dropout率  
    """  
    decoder = nn.Sequential(  
        # 添加dropout层，以防止过拟合  
        nn.Dropout(p_drop),  
        # 第一个线性层，从 latent_size 映射到 hidden_size  
        nn.Linear(latent_size, hidden_size),  
        # 激活函数，增加模型非线性  
        nn.ReLU(),  
        # 再次添加dropout层  
        nn.Dropout(p_drop),  
        # 第二个线性层，保持 hidden_size 不变  
        nn.Linear(hidden_size, hidden_size),  
        # 再次使用激活函数  
        nn.ReLU(),  
        # 第三个dropout层  
        nn.Dropout(p_drop),  
        # 第三个线性层，从 hidden_size 映射到 num_channels * width * height  
        # 这一步是为了将特征展平，方便后续重塑  
        nn.Linear(hidden_size, num_channels * width * height),  
        # 使用 ReshapeLast 层将最后一个维度重塑为 [num_channels, width, height]  
        ReshapeLast((num_channels, width, height)),  
    )  
    return decoder

这样就建立起了一个简单的FFNN：

# 定义一个全连接神经网络解码器，该解码器从10维的潜在编码映射到输出张量  
# 使用该解码器来处理一个形状为(5, 10)的张量，该张量包含5个样本，每个样本的潜在编码是10维的  
# 这里使用了torch.zeros来生成一个所有元素都是0的张量作为示例输入  
  
# 计算解码器输出张量的形状  
output_shape = build_ffnn_decoder(latent_size=10, num_channels=1)(torch.zeros((5, 10))).shape  
  
# build_ffnn_decoder是一个全连接神经网络解码器函数，它接受两个参数：  
# latent_size=10 表示潜在编码的维度是10  
# num_channels=1 表示输出张量的通道数是1  
  
# torch.zeros((5, 10)) 生成一个形状为(5, 10)的张量，其中所有元素都是0  
# 这个张量表示一个批处理大小为5的数据集，每个数据点的潜在编码是一个10维的向量  
  
# build_ffnn_decoder函数将上述张量作为输入，并返回一个输出张量  
# 输出张量的形状取决于解码器的具体结构和num_channels参数  
# 在这里，我们假设解码器会将10维的潜在编码映射到一个具有num_channels个通道的图像上  
# 但具体的宽度和高度需要由解码器的设计决定，这里并未明确给出  
  
# output_shape变量将保存解码器输出张量的形状  
# 例如，如果解码器将10维的潜在编码映射到一个64x64像素的单通道图像上，  
# 那么output_shape将会是torch.Size([5, 1, 64, 64])

torch.Size([5, 1, 64, 64])

FFNN解码器的问题是输出层的大小可能过大。

为了更好地适应我们的数据类型，一个具有适当归纳偏置的架构是卷积神经网络（CNN），特别是转置卷积神经网络（transposed CNN）。接下来，我们将设计一个这样的解码器。

class MySequential(nn.Sequential):
    """
    这是一个 nn.Sequential 的版本，它可以处理结构化批次数据
     （即，具有多个维度的批次数据），
     即使其中的某些 nn 层不支持结构化数据。

    思路是仅将 nn.Sequential 包装在两次 reshape 调用周围，
     这些调用移除并恢复批次维度。
    """

    def __init__(self, *args, event_dims=1):
        super().__init__(*args)  # 调用基类的构造函数
        self._event_dims = event_dims  # 存储事件维度的数量
                
    def forward(self, input):
        # 记录批次形状
        batch_shape = input.shape[:-self._event_dims]
        # 记录事件形状
        event_shape = input.shape[-self._event_dims:]
        # 展平批次形状并获取输出
        output = super().forward(input.reshape((-1,) + event_shape))
        # 恢复批次形状
        return output.reshape(batch_shape + output.shape[1:])


def build_cnn_decoder(latent_size, num_channels, width=64, height=64, hidden_size=1024, p_drop=0.):
    """
    将潜在编码映射到形状为 [num_channels, width, height] 的张量。

    latent_size: 潜在编码的大小
    num_channels: 输出中的通道数
    width: 必须是 64 （目前是这样）
    height: 必须是 64 （目前是这样）
    hidden_size: 我们首先从 latent_size 映射到 hidden_size，
        然后使用转置的 2D 卷积到 [num_channels, width, height]
    p_drop: 线性层之前的 dropout 比率
    """
    if width != 64:
        raise ValueError("The width is hardcoded")  # 如果宽度不是64，抛出异常
    if height != 64:
        raise ValueError("The height is hardcoded")  # 如果高度不是64，抛出异常

    # TODO: 改变架构，使 width 和 height 不是硬编码
    decoder = MySequential(        
        nn.Dropout(p_drop),  # Dropout层
        nn.Linear(latent_size, hidden_size),  # 线性层，从潜在大小到隐藏大小
        ReshapeLast((hidden_size, 1, 1)),  # 重塑最后一层的维度
        nn.ConvTranspose2d(hidden_size, 128, 5, 2),  # 转置卷积层
        nn.ReLU(),  # 激活层
        nn.ConvTranspose2d(128, 64, 5, 2),  # 转置卷积层
        nn.ReLU(),  # 激活层
        nn.ConvTranspose2d(64, 32, 6, 2),  # 转置卷积层
        nn.ReLU(),  # 激活层
        nn.ConvTranspose2d(32, num_channels, 6, 2),  # 转置卷积层
        event_dims=1  # 设置事件维度
    )
    return decoder

# 注释：  
# 使用自定义的MySequential（假设已定义）作为容器，我们可以将解码器设计为接受更复杂的批处理形状。  
# 在这个例子中，我们创建了一个形状为[3, 5, 10]的零张量，其中3可能表示外部批处理大小，  
# 5表示对于每个外部样本，我们都有5个内部样本（例如，多次从潜在空间抽取的样本），  
# 10则是每个内部样本的潜在编码的维度。  
# build_cnn_decoder函数会基于给定的潜在编码维度（latent_size=10）和输出通道数（num_channels=1）  
# 来构建一个卷积神经网络解码器。  
# 最后，我们调用该解码器并传入零张量来检查其输出形状。  
# 注意：这里假设MySequential可以正确处理多维度的输入，并且解码器本身也支持这种输入形状。
build_cnn_decoder(latent_size=10, num_channels=1)(torch.zeros((3, 5, 10))).shape

现在我们准备设计一款适用于图像模型的CPDNet，其核心在于结合一个精心选择的解码器和一个恰当的分布模型。

以下代码定义了两个类，BinarizedImageModel 和 ContinuousImageModel，它们都继承自 CPDNet 类（在代码中没有给出定义）。这两个类分别实现了二值图像模型和连续图像模型，用于定义给定潜在变量 $z$ 下的条件概率分布 $p (X ∣ Z = z)$ 。

class BinarizedImageModel(CPDNet):    
    """
    二值图像模型类，用于定义给定潜在变量 z 的条件概率分布 X|Z=z。
    """
    
    def __init__(self, num_channels, width, height, latent_size, decoder_type=build_ffnn_decoder, p_drop=0.):
        super().__init__((num_channels, width, height))  # 调用基类的构造函数
        # 初始化解码器，将潜在变量映射到图像空间
        self.decoder = decoder_type(
            latent_size=latent_size, 
            num_channels=num_channels,
            width=width,
            height=height,
            p_drop=p_drop
        ) 

    def forward(self, z):
        """
        返回条件概率分布 cpd X|Z=z。

        z: 批次形状 + (潜在维度,)
        """
        # 批次形状 + (通道数, 宽度, 高度)
        h = self.decoder(z)        
        # 返回一个独立分布的伯努利分布
        return td.Independent(td.Bernoulli(logits=h), len(self.outcome_shape))


class ContinuousImageModel(CPDNet):    
    """
    连续图像模型类，用于定义给定潜在变量 z 的条件概率分布 X|Z=z。
    """
    
    # 类的构造函数和 forward 方法与二值图像模型类似，不同之处在于这里使用的是连续伯努利分布
    def __init__(self, num_channels, width, height, latent_size, decoder_type=build_ffnn_decoder, p_drop=0.):
        super().__init__((num_channels, width, height))        
        self.decoder = decoder_type(
            latent_size=latent_size, 
            num_channels=num_channels,
            width=width,
            height=height,
            p_drop=p_drop
        ) 

    def forward(self, z):
        """
        返回条件概率分布 cpd X|Z=z。

        z: 批次形状 + (潜在维度,)
        """
        h = self.decoder(z)        
        # 返回一个独立分布的连续伯努利分布
        return td.Independent(td.ContinuousBernoulli(logits=h), len(self.outcome_shape))

# 以下是使用二值图像模型的示例代码

# 创建观测模型实例
obs_model = BinarizedImageModel(
    num_channels=img_shape[0],
    width=img_shape[1],
    height=img_shape[2],
    latent_size=10,
    p_drop=0.1,
)
print(obs_model)
# 将一批五个 z 映射到 5 个在 [1,64,64]-维二值张量上的分布
print(obs_model(torch.zeros([5, 10])))

# 使用不同的解码器

# 创建使用不同解码器的观测模型实例
obs_model = BinarizedImageModel(
    num_channels=img_shape[0],
    width=img_shape[1],
    height=img_shape[2],
    latent_size=10,     
    p_drop=0.1, 
    decoder_type=build_cnn_decoder
)
print(obs_model)
# 将一批五个 z 映射到 5 个在 [1,64,64]-维二值张量上的分布
print(obs_model(torch.zeros([5, 10])))

2.3 联合概率分布

我们现在可以将先验概率和观测模型融合，形成联合概率分布。联合概率分布能够支持一些关键的操作，例如边缘概率密度的计算、后验概率密度的评估，以及从该分布中进行抽样。进行边缘和后验评估所需的计算可能是可行的，也可能不可行，具体情况如下所述。

通过联合概率密度函数，我们可以使用以下公式计算 $x$ 的边缘概率密度：

$p_X(x|\theta) = \sum_{z \in \mathcal{Z}} p_{ZX}(z,x|\theta) = \sum_{z \in \mathcal{Z}} p_Z(z|\theta) p_{X|Z}(x|z, \theta)$

如果我们假设 $\mathcal{Z}$ 是可数的，那么可以通过枚举的方式来计算边缘概率，所需的时间与 $\mathcal{Z}$ 的大小成线性关系。然而，如果 $\mathcal{Z}$ 是不可数无限集，或者其规模组合上非常大（例如，所有可能的 $K$ 维位向量的空间），那么这种边缘计算将是不可行的。

如果枚举是可行的，我们还可以通过以下公式计算给定 $x$ 条件下 $z$ 的后验概率：

$p_{Z|X}(z|x, \theta) = \frac{p_Z(z|\theta) p_{X|Z}(x|z, \theta)}{p_X(x|\theta)}$

当边缘计算不可行时，我们可以通过直接应用Jensen不等式来获得一个简单的下界估计：

$\log p_X(x|\theta) = \log \sum_{z \in \mathcal{Z}} p_Z(z|\theta) p_{X|Z}(x|z, \theta) \geq \sum_{z \in \mathcal{Z}} p_Z(z|\theta) \log p_{X|Z}(x|z, \theta)$

利用蒙特卡洛方法，我们可以通过以下方式近似上述求和：

$\frac{1}{S} \sum_{s=1}^S \log p_{X|Z}(x|z_s, \theta) \quad \text{其中 } z_s \sim p_Z$

通过重要性采样，我们可以得到一个更优的下界估计，但这需要我们训练一个近似分布，正如我们在变分推断中所做的那样。

需要记住的是，给定一个数据集 $\mathcal{D}$ ，对数似然函数 $\mathcal{L}(\theta|\mathcal{D}) = \sum_{x \in \mathcal{D}} \log p_X(x|\theta)$ 需要进行边缘概率密度的评估。如果精确的边缘计算不可行，我们就无法评估 $\mathcal{L}(\theta|\mathcal{D})$ 以及它对 $\theta$ 的梯度。如果先验概率是固定的，我们可以使用上述简单的下界来估计梯度，但这种直接应用Jensen不等式的方法通常会产生一个宽松的界限。

下面定义了一个名为 JointDistribution 的类，它封装了先验网络和条件概率分布（cpd）网络来创建一个联合概率分布。这个类提供了一些方法来处理联合分布，包括抽样、计算边缘概率和后验概率，以及估计对数边缘密度的下界。

class JointDistribution(nn.Module):
    """
    一个包装器，用于将先验网络和条件概率分布网络结合起来形成一个联合分布。
    """

    def __init__(self, prior_net: PriorNet, cpd_net: CPDNet):
        """
        prior_net: 参数化 p_Z 的对象
        cpd_net: 参数化 p_{X|Z=z} 的对象
        """
        super().__init__()
        self.prior_net = prior_net
        self.cpd_net = cpd_net

    def prior(self, shape):
        return self.prior_net(shape)

    def obs_model(self, z):
        return self.cpd_net(z)

    def sample(self, shape):
        """
        通过 prior_net(shape).sample() 返回 z，
        并通过 cpd_net(z).sample() 返回 x。
        """
        pz = self.prior_net(shape)
        z = pz.sample()
        px_z = self.cpd_net(z)
        x = px_z.sample()
        return z, x

    def log_prob(self, z, x):
        """
        评估联合结果的对数概率密度。
        """
        batch_shape = z.shape[:-len(self.prior_net.outcome_shape)]        
        pz = self.prior_net(batch_shape)        
        px_z = self.cpd_net(z)
        return pz.log_prob(z) + px_z.log_prob(x)

    def log_marginal(self, x, enumerate_fn):
        """
        返回 x 的对数边缘密度。
        
        enumerate_fn: 枚举先验支持的功能
            （这对于边缘化 p(x) = \int p(z, x) dz 是必要的）

            如果支持是一个（小的）可数有限集，这是有意义的。在这种情况下，可以使用
                enumerate=lambda p: p.enumerate_support()
            例如，Categorical 和 OneHotCategorical 支持此功能。

            如果支持是离散的（例如，位向量），你仍然可以明确地枚举它，但你需要编写自定义代码，
            因为 torch.distributions 不会为你提供该功能。

            如果支持是不可数的、可数无限大的，或者无论如何都很大，
            你需要近似工具（例如变分推断、重要性采样等）。
        """
        batch_shape = x.shape[:-len(self.cpd_net.outcome_shape)]
        pz = self.prior_net(batch_shape)        
        log_joint = []
        z = enumerate_fn(pz)
        px_z = self.cpd_net(z)
        log_joint = pz.log_prob(z) + px_z.log_prob(x.unsqueeze(0))
        return torch.logsumexp(log_joint, 0)

    def posterior(self, x, enumerate_fn):
        """
        返回后验分布 Z|X=x。
        
        由于代码是离散的，我们通过 `enumerate_fn` 提供的穷尽枚举，
        返回所有可能潜在代码空间上的离散分布。
        """
        batch_shape = x.shape[:-len(self.cpd_net.outcome_shape)]        
        pz = self.prior_net(batch_shape)        
        z = enumerate_fn(pz)
        px_z = self.cpd_net(z)
        log_joint = pz.log_prob(z) + px_z.log_prob(x.unsqueeze(0))
        log_joint = torch.swapaxes(log_joint, 0, -1)
        return td.Categorical(logits=log_joint)

    def naive_lowerbound(self, x, num_samples: int):
        """
        返回 x 的对数边缘密度的 MC 下界：
            log p(x) >= 1/S \sum_s log p(x|z[s])
                其中 z[s] ~ p_Z
        """
        batch_shape = x.shape[:-len(self.cpd_net.outcome_shape)]
        pz = self.prior_net(batch_shape)
        log_probs = []
        for z in pz.sample((num_samples,)): 
            px_z = self.cpd_net(z)
            log_probs.append(px_z.log_prob(x))
        log_probs = torch.stack(log_probs)
        return torch.mean(log_probs, 0)

# 以下是测试联合分布的函数
def test_joint_dist(latent_size=10, data_shape=(1, 64, 64), batch_size=2, hidden_size=32):    
    # 测试二值数据的模型
    # ...（此处省略了部分代码，遵循上述类定义的逻辑）
    # 测试连续数据的模型
    # ...（此处省略了部分代码，遵循上述类定义的逻辑）

# 调用测试函数
test_joint_dist(10)

3. 学习过程

在训练过程中，我们采用基于随机梯度的最大似然估计法来估计模型参数 $\theta$ 。对于可处理的模型，我们首先评估其对数似然函数：

$\begin{aligned} \mathcal{L}(\theta|\mathcal{D}) &= \sum_{x \in \mathcal{D}} \log p_X(x|\theta) \end{aligned}$

其中， $\mathcal{D}$ 表示训练数据集， $p_X(x|\theta)$ 表示给定参数 $\theta$ 下数据 $x$ 的概率。

接着，我们利用随机小批量数据来估计对数似然函数关于参数 $\theta$ 的梯度：

$\begin{aligned} \nabla_{\theta}\mathcal{L}(\theta|\mathcal{D}) &\approx \frac{1}{S} \sum_{s=1}^{S} \nabla_{\theta}\log p_X(x^{(s)}|\theta) \\ &\text{其中，} x^{(s)} \text{ 是从数据集 } \mathcal{D} \text{ 中随机抽取的样本} \end{aligned}$

通过这种方式，我们可以利用小批量数据来近似计算整个数据集上的梯度，从而加速模型的训练过程。

3.1 可操作的潜变量模型（LVMs）

一个由 $K$ 个组件组成的混合模型在本质上是一个可操作的潜变量模型（LVM）：

$\begin{aligned} p_X(x|\theta) &= \frac{1}{K} \sum_{z=1}^K p_{X|Z}(x|z, \theta) \end{aligned}$

在这个模型中， $p_{X|Z=z}$ 是基于 $z$ 的独热编码的图像模型。

# 创建一个联合分布对象，该对象结合了先验网络（prior_net）和条件概率分布网络（cpd_net）  
print(JointDistribution(  
    # 先验网络：一个分类先验网络，假设有10个类别（或称为潜在变量/隐变量）  
    prior_net=CategoricalPriorNet(10),  
      
    # 条件概率分布网络（CPDNet）：用于从给定的潜在变量生成图像  
    cpd_net=BinarizedImageModel(  
        # 图像通道数，例如RGB图像为3，灰度图像为1  
        num_channels=img_shape[0],  
        # 图像的宽度  
        width=img_shape[1],  
        # 图像的高度  
        height=img_shape[2],  
        # 潜在变量的维度大小，与先验网络中的类别数相对应  
        latent_size=10,  
        # 使用的解码器类型，这里使用build_ffnn_decoder函数来构建解码器  
        # 假设build_ffnn_decoder是一个函数，它返回一个全连接神经网络（FFNN）解码器  
        decoder_type=build_ffnn_decoder  
    )  
))

3.2 训练流程

以下是用于通过精确的对数似然函数来评估和训练潜变量模型（LVM）的详细训练流程及其辅助代码。

def assess_exact(model: JointDistribution, enumerate_fn, dl, device):
    """
    用于估计模型对数似然的包装器。
    数据样本是数据加载器中的所有数据点。

    model: 可以对 Z 进行精确边缘化的联合分布
    enumerate_fn: 用于枚举一批数据的 Z 支持的算法
        将用于评估 `model.log_prob(batch, enumerate_fn)`
    dl: torch 数据加载器
    device: torch 设备
    """
    L = 0
    data_size = 0
    with torch.no_grad():  # 禁用梯度计算
        for batch_x, batch_y in dl:  # 遍历数据加载器中的批次
            # 计算并累加对数边缘概率
            L = L + model.log_marginal(batch_x.to(device), enumerate_fn).sum(0)
            data_size += batch_x.shape[0]  # 更新数据点数量
    L = L / data_size  # 计算平均对数似然
    return L

# ...

def train_exact(model: JointDistribution, enumerate_fn, optimiser, 
    training_data, dev_data,
    batch_size=64, num_epochs=10, check_every=10,    
    grad_clip=5.,
    report_metrics=['L'],
    num_workers=2,
    device=torch.device('cuda:0')
    ):
    """
    model: 可以对 Z 进行精确边缘化的联合分布
    enumerate_fn: 用于枚举 Z 支持的功能
        （与 model.log_prob 结合使用）
    optimiser: pytorch 优化器
    training_data: 训练用的 torchvision 数据集
    dev_data: 验证用的 torchvision 数据集
    batch_size: 根据你的内存量可以设置更大
    num_epochs: 更多的迭代次数可以提高收敛性
    check_every: 设定检查开发集性能的频率
    device: 运行实验的设备

    返回一个日志，记录了训练期间计算的数量（用于绘图）
    """
    # 创建训练和验证的数据加载器
    batcher = DataLoader(training_data, batch_size, shuffle=True, num_workers=num_workers, pin_memory=True)
    dev_batcher = DataLoader(dev_data, batch_size, num_workers=num_workers, pin_memory=True)

    total_steps = num_epochs * len(batcher)  # 总步数
    log = defaultdict(list)  # 记录训练和验证的日志

    step = 0
    model.eval()  # 评估模式
    
    # 在设备上评估开发集的对数似然
    log['dev.L'].append((step, assess_exact(model, enumerate_fn, dev_batcher, device=device).item()))

    # 使用 tqdm 进度条进行训练
    with tqdm(range(total_steps)) as bar:
        for epoch in range(num_epochs):
            for batch_x, batch_y in batcher:
                model.train()  # 训练模式
                optimiser.zero_grad()  # 清零梯度

                # 计算损失并反向传播
                loss = - model.log_marginal(batch_x.to(device), enumerate_fn).mean(0)
                log['loss'].append((step, loss.item()))
                loss.backward()

                # 梯度裁剪
                nn.utils.clip_grad_norm_(model.parameters(), grad_clip)
                optimiser.step()

                # 更新进度条
                bar_dict = OrderedDict()
                bar_dict['loss'] = f"{loss.item():.2f}"
                bar_dict[f"dev.L"] = "{:.2f}".format(log[f"dev.L"][-1][1])
                bar.set_postfix(bar_dict)
                bar.update()

                # 定期在开发集上评估性能
                if step % check_every == 0:
                    model.eval()
                    log['dev.L'].append((step, assess_exact(model, enumerate_fn, dev_batcher, device=device).item()))

                step += 1

    model.eval()  # 评估模式
    # 记录最终的对数似然
    log['dev.L'].append((step, assess_exact(model, enumerate_fn, dev_batcher, device=device).item()))

    return log

以下是用于检查从混合模型中抽取样本的辅助函数或代码片段。

def inspect_mixture_model(model: JointDistribution, support_size):  
    # 从先验分布中抽取一些样本进行展示  
    # _, x_ = model.sample((support_size, 5))  # 这行代码原样保留，但可能需要根据实际函数进行调整  
    # 假设这里从模型中抽取的样本是图像，并且我们将其重塑为合适的形状  
    # x_ = x_.cpu().reshape(-1, 1, 64, 64)  # 将数据移至CPU并重新整形为图像格式  
  
    # 创建一个绘图窗口并设置其大小  
    plt.figure(figsize=(12,6))  
  
    # 关闭坐标轴显示  
    plt.axis('off')  
  
    # 使用make_grid函数将多个图像合并为一个网格，并重新排列其维度以便可视化  
    # 注意：make_grid函数通常来自torchvision.utils  
    plt.imshow(make_grid(x_, nrow=support_size).permute((1, 2, 0)))  
  
    # 设置图的标题为“先验样本”  
    plt.title("先验样本")  
  
    # 显示图像  
    plt.show()  
  
    # 接下来，从每个组件中抽取样本进行展示  
    # support_size 是抽取的样本数量，latent_dim 是潜在空间的维度（但在此代码中未直接使用）  
    # support = model.prior(tuple()).enumerate_support()  # 这行代码假设可以枚举先验分布的支持集  
  
    # 假设我们从每个组件中抽取了5个样本，并将它们重塑为图像格式  
    # 注意：这里假设obs_model是一个可以从给定潜在变量生成图像的方法  
    # x_ = model.obs_model(support).sample((5,)).cpu().reshape(-1, 1, 64, 64)  
  
    # 创建一个新的绘图窗口并设置其大小  
    plt.figure(figsize=(12,6))  
  
    # 再次关闭坐标轴显示  
    plt.axis('off')  
  
    # 使用make_grid函数将多个图像合并为一个网格，并重新排列其维度以便可视化  
    plt.imshow(make_grid(x_, nrow=support_size).permute((1, 2, 0)))  
  
    # 设置图的标题为“组件样本”  
    plt.title("组件样本")  
  
    # 显示图像  
    plt.show()

3.2.1.实验验证

# 确保实验的可复现性，通过设置随机种子。
seed_all()

# 创建一个联合分布模型，该模型由先验网络和条件概率分布网络组成。
mixture_model = JointDistribution(
    # 先验网络，这里使用的是CategoricalPriorNet，它生成类别分布，参数为潜在类别的数量。
    prior_net=CategoricalPriorNet(10),
    # 条件概率分布网络，这里使用的是BinarizedImageModel，它处理图像数据。
    # 这个网络可能是二值化的（binary），也可能是连续的（continuous），具体取决于数据预处理。
    cpd_net=BinarizedImageModel(
        num_channels=img_shape[0],  # 图像的通道数。
        width=img_shape[1],  # 图像的宽度。
        height=img_shape[2],  # 图像的高度。
        latent_size=10,  # 潜在变量的维度。
        # 解码器的构建函数，这里使用的是全连接神经网络（feed-forward neural network）。
        decoder_type=build_ffnn_decoder,
        # 网络中的dropout比例。
        p_drop=0.1,
    )
).to(my_device)  # 将模型移动到指定的设备上，例如GPU。

# 打印模型的摘要信息。
print(mixture_model)

# 创建模型的优化器，这里使用的是Adam优化器。
# 优化器会遍历模型的所有参数，并使用给定的学习率和权重衰减系数进行优化。
mm_optim = opt.Adam(mixture_model.parameters(), lr=1e-3, weight_decay=1e-6)

# 调用train_exact函数来训练混合模型。
# model参数是之前初始化的混合模型。
# optimiser参数是模型的优化器。
# enumerate_fn是一个函数，用于枚举模型的支持点。
# training_data是训练数据集。
# dev_data是开发/验证数据集。
# batch_size是每个训练批次的样本数量。
# num_epochs是训练周期数，更多的周期有助于模型更好地学习数据。
# check_every是检查频率，即每隔多少步在开发集上评估一次模型。
# grad_clip是梯度裁剪的阈值，用于防止梯度爆炸。
# device是模型运行的设备，例如GPU。
log = train_exact(
    model=mixture_model,
    optimiser=mm_optim,
    enumerate_fn=lambda p: p.enumerate_support(),
    training_data=train_ds,
    dev_data=val_ds,
    batch_size=256,
    num_epochs=1,  # 用更多的周期可以得到更好的模型性能
    check_every=10,
    grad_clip=5.,
    device=my_device
)

# 创建一个图形和两个子图，用于绘制训练损失和开发集上的对数似然。
# sharex=True表示两个子图共享x轴，sharey=False表示不共享y轴。
# figsize设置图形的大小。
fig, axs = plt.subplots(1, 2, sharex=True, sharey=False, figsize=(12, 3))

# 绘制训练损失。取日志中'loss'键对应的数据，绘制其第一列（步骤）和第二列（损失值）。
_ = axs[0].plot(np.array(log['loss'])[:, 0], np.array(log['loss'])[:, 1])
# 设置第一个子图的y轴标签为"training loss"。
_ = axs[0].set_ylabel("training loss")
# 设置第一个子图的x轴标签为"steps"。
_ = axs[0].set_xlabel("steps")

# 绘制开发集上的对数似然。取日志中'dev.L'键对应的数据，绘制其第一列（步骤）和第二列（对数似然值）。
_ = axs[1].plot(np.array(log['dev.L'])[:, 0], np.array(log['dev.L'])[:, 1])
# 设置第二个子图的y轴标签为"dev L"。
_ = axs[1].set_ylabel("dev L")
# 设置第二个子图的x轴标签为"steps"。
_ = axs[1].set_xlabel("steps")

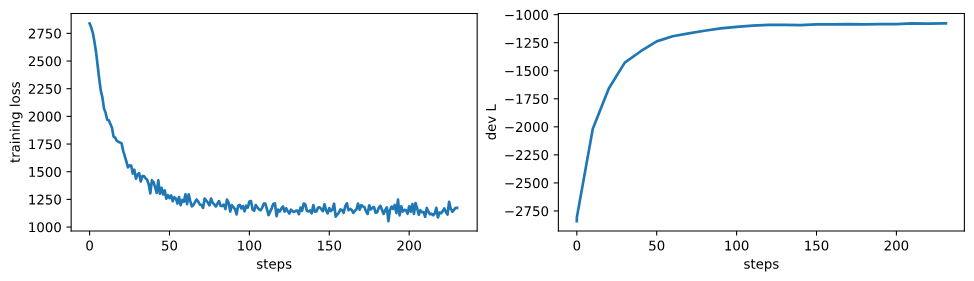
在这里插入图片描述

inspect_mixture_model(mixture_model, 10)

在这里插入图片描述

混合模型在表达观测模型的能力上相当有限，它最多只能将数据空间分割成 $K$ 个不同的群组。

然而，因子模型则赋予了观测模型高达 $2^K$ 种不同的编码可能性。接下来，我们将构建一个因子模型来克服这一限制。

3.3 难以求解的潜在变量模型（LVMs）

在某些情况下，对潜在变量进行边缘化处理变得非常复杂（例如，当潜在空间 $\mathcal{Z}$ 是一个 $K$ 维度的二进制向量空间，且 $K$ 的值适中）或者实际上不可行（例如，当 $\mathcal{Z}$ 是一个从 1 到 $K$ 的整数集合，且 $K$ 很大，如 $K > 10$ ）。这时，我们会采用变分推断的方法，引入一个参数化的近似后验分布 $q_{Z|X=x}$ 来估计模型的真实后验分布 $p_{Z|X=x}$ ，并通过最大化证据下界（ELBO）来估计这个近似和联合分布。对于单个观测值 $x$ ，ELBO 公式如下：

$\mathcal{E}(\lambda, \theta | \mathcal{D}) = \mathbb{E}_{x \sim \mathcal{D}}\left[ \mathbb{E}\left[\log \frac{ p_{ZX}(z, x|\theta)}{q_{Z|X}(z|x, \lambda)}\right] \right]$

$\left( \mathbb{E}_{x \sim \mathcal{D}}\left[ \mathbb{E}[ \log p_{ZX}(x|z,\theta)] \right] \right) - \left( \mathbb{E}_{x \sim \mathcal{D}}\left[ \mathrm{KL}(q_{Z|X=x}||p_Z) \right] \right)$

这里，内部期望是针对 $q_{Z|X}(z|x, \lambda)$ 来计算的。

当我们根据数据分布来计算期望时，ELBO 的两个部分，即期望的对数似然 $\mathbb{E}[ \log p_{ZX}(x|z,\theta)]$ 和 Kullback-Leibler 散度项 $\mathrm{KL}(q_{Z|X=x}||p_Z)$ ，与信息论中的两个量——失真和速率有关。

我们选择的近似分布应满足以下条件：其支持集应包含在先验分布的支持集中，它应足够简单以便于进行抽样，并且足够简单以便于计算样本的质量。如果可能的话，我们还希望它使得其他量（如熵、相对熵）也是容易计算的。

对于多变量 $z$ ，我们通常选择一个分解式的概率分布族。例如，如果 $z$ 是一个 $D$ 维的位向量，则可能选择如下形式的分布：

$q_{Z|X}(z|x, \lambda) = \prod_{k=1}^K \mathrm{Bernoulli}(z_k|g_k(x;\lambda))$

其中 $\mathbf{g}(x;\lambda)$ 位于区间 (0,1) 的 $K$ 维空间内。这种假设被称为均场近似。

对于分类变量 $z$ ，原则上边缘化是可行的（它需要的时间与可能的分类数 $K$ 成线性关系），但对于一些解码器来说，即使 $K$ 次前向计算也可能太多，因此我们使用一个独立参数化的分类分布：
$q_{Z|X}(z|x, \lambda) = \mathrm{Categorical}(z|\mathbf{g}(x;\lambda))$

其中 $\mathbf{g}(x;\lambda)$ 位于 $K - 1$ 维的简单形空间 $\Delta_{K-1}$ 内。

3.4 推断模型

为了构建推断模型，我们设计了一个条件概率分布网络（CPD nets），该网络用于模拟潜变量的条件分布。

在进行下一步之前，我们首先需要设计一个“编码器”，其功能是将图像 $\in \mathcal{X}$ 映射到一个固定大小的向量上，这个向量可以作为图像 $x$ 的紧凑表示。接下来，我们将开发两种编码器：一种基于全连接神经网络（FFNNs），另一种基于卷积神经网络（CNNs）。

class FlattenImage(nn.Module):
    def forward(self, input):
        # 将输入数据展平为 (batch_size, -1) 的形状
        return input.reshape(input.shape[:-3] + (-1,))

def build_ffnn_encoder(num_channels, width=64, height=64, output_size=1024, p_drop=0.):
    # 使用全连接层构建编码器
    encoder = nn.Sequential(
        FlattenImage(),  # 展平图像
        nn.Dropout(p_drop),  # dropout层
        nn.Linear(num_channels * width * height, output_size//2),  # 线性层
        nn.ReLU(),  # ReLU激活函数
        nn.Dropout(p_drop),  # dropout层
        nn.Linear(output_size//2, output_size//2),  # 线性层
        nn.ReLU(),  # ReLU激活函数
        nn.Dropout(p_drop),  # dropout层
        nn.Linear(output_size//2, output_size),  # 线性层
    )
    return encoder

def build_cnn_encoder(num_channels, width=64, height=64, output_size=1024, p_drop=0.):
    # 检查是否修改了硬编码的参数
    if width != 64 or height != 64 or output_size != 1024:
        raise ValueError("The width, height, and output_size are hardcoded")
    # 使用卷积层构建编码器
    encoder = MySequential(
        nn.Conv2d(num_channels, 32, 4, 2),  # 卷积层
        nn.LeakyReLU(0.2),  # 泄漏ReLU激活函数
        nn.Conv2d(32, 64, 4, 2),  # 卷积层
        nn.LeakyReLU(0.2),  # 泄漏ReLU激活函数
        nn.Conv2d(64, 128, 4, 2),  # 卷积层
        nn.LeakyReLU(0.2),  # 泄漏ReLU激活函数
        nn.Conv2d(128, 256, 4, 2),  # 卷积层
        nn.LeakyReLU(0.2),  # 泄漏ReLU激活函数
        FlattenImage(),  # 展平图像
        event_dims=3  # 设置事件维度
    )
    return encoder

# 以下是使用构建的编码器的示例代码

# 使用全连接神经网络编码器处理一批五个 [1, 64, 64] 维的图像
# 将它们编码为五个 1024 维的向量
build_ffnn_encoder(num_channels=1)(torch.zeros((5, 1, 64, 64))).shape

# 结构化批次数据示例 (这里尝试使用 (3,5) 批次形状)
build_ffnn_encoder(num_channels=1)(torch.zeros((3, 5, 1, 64, 64))).shape

# 使用卷积神经网络编码器处理一批五个 [1, 64, 64] 维的图像
# 将它们编码为五个 1024 维的向量
build_cnn_encoder(num_channels=1)(torch.zeros((5, 1, 64, 64))).shape

# 由于使用了 MySequential，我们也可以处理结构化批次数据
# (这里尝试使用 (3,5) 批次形状)
build_cnn_encoder(num_channels=1)(torch.zeros((3, 5, 1, 64, 64))).shape

接下来，我们可以设计一些条件概率分布网络（CPD nets），这些网络能够将图像的编码映射到关于 $\mathcal{Z}$ 的概率质量函数（pmf）。

伯努利乘积模型

这种模型适用于参数化固定维度二进制向量的条件概率分布。

独热分类模型

这种模型则用于参数化来自有限集合的类别的独热编码的条件概率分布。

代码定义了几个类，包括 BernoulliCPDNet 和 CategoricalCPDNet，它们都继承自 CPDNet 类（在代码中没有给出定义）。这些类实现了条件概率分布网络，用于建模给定输入下潜在变量的分布。此外，还有一个 test_cpds 函数用于测试这些网络，以及一个 InferenceModel 类，用于结合编码器和条件概率分布网络进行推断。

class BernoulliCPDNet(CPDNet):
    """
    输出分布是伯努利分布的乘积。
    """
    
    def __init__(self, outcome_shape, num_inputs: int, hidden_size: int=None, p_drop: float=0.):
        """
        outcome_shape: 结果的形状（整数或元组）
            如果是整数，我们将其转换为单例元组
        num_inputs: forward 输入的最右边的维度
        hidden_size: CPDNet 的隐藏层大小（如果跳过则使用 None）
        p_drop: 在每个 Linear 层之前的 dropout 配置
        """
        # ...（类的其余代码）

    def forward(self, inputs):        
        # 计算并返回伯努利分布的独立性
        h = self.encoder(inputs)
        return td.Independent(td.Bernoulli(logits=self.logits(h)), len(self.outcome_shape))

class CategoricalCPDNet(CPDNet):
    """
    输出分布是分类分布的乘积。
    """
    # 类的构造函数与 BernoulliCPDNet 类似，不同之处在于输出分布

    def forward(self, inputs):        
        # 计算并返回分类分布
        h = self.encoder(inputs)
        return td.OneHotCategorical(logits=self.logits(h))

# 以下是测试条件概率分布网络的函数

def test_cpds(outcome_shape, batch_size=3, input_dim=5, hidden_size=2):
    # 测试伯努利条件概率分布网络
    cpd_net = BernoulliCPDNet(outcome_shape, num_inputs=input_dim, hidden_size=hidden_size) 
    # ...（函数的其余代码）

# 测试不同的网络配置
test_cpds(12)
test_cpds(12, hidden_size=None)
test_cpds((4, 5))

# 以下是结合编码器和条件概率分布网络的推断模型类

class InferenceModel(CPDNet):
    def __init__(self, cpd_net_type, 
                 latent_size, num_channels=1, width=64, height=64, 
                 hidden_size=1024, p_drop=0., 
                 encoder_type=build_ffnn_encoder):        
        super().__init__(latent_size)
        
        self.latent_size = latent_size    
        # 将图像编码为 hidden_size 维的向量
        self.encoder = encoder_type(
            num_channels=num_channels,
            width=width, 
            height=height,
            output_size=hidden_size,
            p_drop=p_drop
        )
        # 从 hidden_size 维的编码映射到 Z|X=x 的 cpd
        self.cpd_net = cpd_net_type(
             latent_size, 
             num_inputs=hidden_size, 
             hidden_size=2*latent_size,
             p_drop=p_drop
        )
    
    def forward(self, x):
        # 执行推断模型的前向传播
        h = self.encoder(x)        
        return self.cpd_net(h)

最后但同样关键的是，我们可以将编码器与我们选择的条件概率分布网络（CPD net）相结合。

3.5 神经变分推断

在训练我们的生成模型时，我们将采用变分推断方法，这需要同时训练一个推断模型。为了实现这一目标，我们将使用ELBO（证据下界）作为目标函数，并基于得分函数估计法来计算梯度。

尽管传统的变分自编码器（VAE）采用了不同的生成模型和梯度估计器，但在现代文献中，我们常常将这种结合了神经网络和变分推断的模型统称为变分自编码器。

对于给定的数据点 $x$ ，我们将通过蒙特卡洛估计法来计算ELBO关于 $\lambda$ 的梯度，其表达式如下：

$\nabla_{\lambda} \mathcal{E}(\lambda, \theta|x) = \mathbb{E}\left[ r(z, x; \theta, \lambda) \nabla_{\lambda}\log \frac{p_{ZX}(z, x|\theta)}{q_{Z|X}(z|x, \lambda)} \right]$

其中，“奖励”函数 $r$ 定义为：

$\theta, \lambda) = \log p_{X|Z}(x|z, \theta)$

然而，由于这个梯度估计器可能会产生较大的噪声，因此通常通过引入控制变量来改进奖励函数的估计。控制变量通常是关于 $x$ 、 $\theta$ 和 $\lambda$ 的函数，但不依赖于我们评估奖励函数的动作 $z$ 。我们将实现这些控制变量作为奖励函数的包装器。接下来，我们将确定控制变量的API设计。

class VarianceReduction(nn.Module):
    """
    我们将使用简单的控制变量形式来减少方差。
    这些是对奖励的变换，它们独立于采样的潜在变量，
    但理论上可以依赖于x，以及生成模型和推断模型的参数。

    其中一些是可训练的组件，因此它们也对损失有所贡献。
    """

    def __init__(self):
        super().__init__()

    def forward(self, r, x, q, r_fn):
        """
        返回变换后的奖励和对损失的贡献。

        r: 一批奖励
        x: 一批观测数据
        q: 策略
        r_fn: 奖励函数
        """
        return r, torch.zeros_like(r)

# ...

class NVIL(nn.Module):
    """
    一个生成模型 p(z)p(x|z) 和一个对该模型真实后验 p(z|x) 的近似 q(z|x)。

    近似是为了最大化ELBO 而估计的，联合分布也是如此。
    """

    def __init__(self, gen_model: JointDistribution, inf_model: InferenceModel, cv_model: VarianceReduction):
        """
        gen_model: 生成模型 p(z)p(x|z)
        inf_model: 近似后验 q(z|x)，用于近似 p(z|x)
        cv_model: 奖励的可选变换
        """
        super().__init__()
        self.gen_model = gen_model        
        self.inf_model = inf_model
        self.cv_model = cv_model

    # 以下是模型参数的获取方法

    def gen_params(self):
        return self.gen_model.parameters()

    def inf_params(self):
        return self.inf_model.parameters()

    def cv_params(self):
        return self.cv_model.parameters()

    # 以下是采样和条件采样的方法

    def sample(self, batch_size, sample_size=None, oversample=False):
        # 从联合分布中采样
        # ...
        pz = self.gen_model.prior((batch_size,))
        samples = [None] * (sample_size or 1)        
        px_z = self.gen_model.obs_model(pz.sample()) if oversample else None
        for k in range(sample_size or 1):
            if not oversample:
                px_z = self.gen_model.obs_model(pz.sample())
            samples[k] = px_z.sample()
        x = torch.stack(samples) 
        return x if sample_size else x.squeeze(0)

    def cond_sample(self, x, sample_size=None, oversample=False):
        # 给定 x 条件下的采样
        # ...
        qz = self.inf_model(x)
        samples = [None] * (sample_size or 1)        
        px_z = self.gen_model.obs_model(qz.sample()) if oversample else None        
        for k in range(sample_size or 1):
            if not oversample:
                px_z = self.gen_model.obs_model(qz.sample())
            samples[k] = px_z.sample()        
        x = torch.stack(samples) 
        return x if sample_size else x.squeeze(0)

    # 以下是计算联合概率密度的方法

    def log_prob(self, z, x):
        # 在生成模型下的联合结果的对数概率密度
        # ...
        return self.gen_model.log_prob(z=z, x=x)

    # 以下是NVIL模型中使用的方法

    def DRL(self, x, sample_size=None):
        """
        基于单个数据点但多个潜在样本的模型的
            * 失真 D
            * 速率 R
            * 对数似然 L
        的蒙特卡洛估计。
        """
        sample_size = sample_size or 1
        obs_dims = len(self.gen_model.cpd_net.outcome_shape)
        batch_shape = x.shape[:-obs_dims]
        with torch.no_grad():        
            qz = self.inf_model(x)
            pz = self.gen_model.prior(batch_shape)
            R = td.kl_divergence(qz, pz)
            D = 0
            ratios = [None] * sample_size
            for k in range(sample_size):
                z = qz.sample()
                px_z = self.gen_model.obs_model(z)
                ratios[k] = pz.log_prob(z) + px_z.log_prob(x) - qz.log_prob(z)
                D = D - px_z.log_prob(x)
            ratios = torch.stack(ratios, dim=-1)
            L = torch.logsumexp(ratios, dim=-1) - np.log(sample_size)            
            D = D / sample_size
            return D, R, L
        # ...

    def elbo(self, x, sample_size=None):
        """
        ELBO 的蒙特卡洛估计 = -D -R
        """
        # ...
        D, R, _ = self.DRL(x, sample_size=sample_size)
        return -D -R

    def log_prob_estimate(self, x, sample_size=None):
        """
        重要性采样估计的对数 p(x)
        """
         _, _, L = self.DRL(x, sample_size=sample_size)
        return L


    def forward(self, x, sample_size=None, rate_weight=1.):
        """
        蒙特卡洛估计 - grad ELBO 的替代品

        x: [batch_size] + data_shape
        sample_size: 如果是1或更多，我们使用多个样本
            sample_size 控制顺序计算（for循环）
        cv: 用于减少方差的可选模块
        """
       sample_size = sample_size or 1
        obs_dims = len(self.gen_model.cpd_net.outcome_shape)
        batch_shape = x.shape[:-obs_dims]

        qz = self.inf_model(x)
        pz = self.gen_model.prior(batch_shape)
        D = 0
        sfe = 0
        reward = 0
        cv_reward = 0
        raw_r = 0
        cv_loss = 0
        for _ in range(sample_size):            
            z = qz.sample()                
            px_z = self.gen_model.obs_model(z)
            raw_r = px_z.log_prob(x) + pz.log_prob(z) - qz.log_prob(z)                
            r, l = self.cv_model(raw_r.detach(), x=x, q=qz, r_fn=lambda a: self.gen_model(a).log_prob(x))
            cv_loss = cv_loss + l
            sfe = sfe + r.detach() * qz.log_prob(z) 
            D = D - px_z.log_prob(x)
        D = (D / sample_size)
        sfe = (sfe / sample_size)
        R = td.kl_divergence(qz, pz)
        cv_loss = cv_loss / sample_size
        
        elbo_grad_surrogate = (-D + sfe)        
        loss = -elbo_grad_surrogate + cv_loss

        return {'loss': loss.mean(0), 'ELBO': (-D -R).mean(0).item(), 'D': D.mean(0).item(), 'R': R.mean(0).item(), 'cv_loss': cv_loss.mean(0).item()}

以下是一个示例


nvil = NVIL(
    JointDistribution(
        BernoulliPriorNet(10),
        BinarizedImageModel(
            num_channels=img_shape[0],
            width=img_shape[1],
            height=img_shape[2],
            latent_size=10,     
            p_drop=0.1,
            decoder_type=build_ffnn_decoder
        )
    ),
    InferenceModel(
        cpd_net_type=BernoulliCPDNet,
        latent_size=10, 
        num_channels=img_shape[0], 
        width=img_shape[1], 
        height=img_shape[2],        
        encoder_type=build_ffnn_encoder
    ),
    VarianceReduction()
)
nvil
for x, y in train_loader:
    print('x.shape:', x.shape)
    print(nvil(x))
    break

3.5.1 训练算法

由于存在多达三个组件（其中某些控制变量可能具有其自己的参数），因此我们需要同时操作多达三个优化器。

class OptCollection:
    # 初始化OptCollection类的一个实例。
    # gen: 表示生成器(generator)的优化器。
    # inf: 表示判别器(inferior)的优化器。
    # cv: 可选参数，表示其他组件的优化器，如果存在的话。
    def __init__(self, gen, inf, cv=None):
        self.gen = gen  # 存储生成器的优化器
        self.inf = inf  # 存储判别器的优化器
        self.cv = cv    # 存储其他组件的优化器，如果没有则为None

    # 零化所有优化器的梯度。
    # 这通常在开始反向传播之前调用。
    def zero_grad(self):
        self.gen.zero_grad()  # 零化生成器优化器的梯度
        self.inf.zero_grad()  # 零化判别器优化器的梯度
        if self.cv:            # 如果存在其他组件的优化器
            self.cv.zero_grad()  # 零化其他组件优化器的梯度

    # 更新所有优化器的参数。
    # 这通常在完成反向传播后调用。
    def step(self):
        self.gen.step()  # 更新生成器优化器的参数
        self.inf.step()  # 更新判别器优化器的参数
        if self.cv:       # 如果存在其他组件的优化器
            self.cv.step()  # 更新其他组件优化器的参数

以下是用于评估和训练模型的辅助代码段。

from collections import defaultdict, OrderedDict
from tqdm.auto import tqdm

# 评估模型的函数，用于估计模型的ELBO、失真度（Distortion）、速率（Rate）和对数似然（Log-likelihood）。
def assess(model, sample_size, dl, device):
    """
    使用数据加载器中的所有数据点来估计模型的ELBO、失真度、速率和对数似然的包装器。
    """
    # 初始化变量
    D = 0  # 失真度
    R = 0  # 速率
    L = 0  # 对数似然
    data_size = 0  # 数据量
    # 不计算梯度
    with torch.no_grad():
        for batch_x, batch_y in dl:  # 遍历数据加载器
            # 调用模型的DRL函数计算当前批次的D、R、L
            Dx, Rx, Lx = model.DRL(batch_x.to(device), sample_size=sample_size)
            # 累加结果
            D = D + Dx.sum(0)
            R = R + Rx.sum(0)
            L = L + Lx.sum(0)
            data_size += batch_x.shape[0]  # 更新数据量
    # 计算平均值
    D = D / data_size
    R = R / data_size
    L = L / data_size
    return {'ELBO': (-D - R).item(), 'D': D.item(), 'R': R.item(), 'L': L.item()}

# 训练VAE模型的函数。
def train_vae(model: NVIL, opts: OptCollection, 
    training_data, dev_data,
    batch_size=64, num_epochs=10, check_every=10,
    sample_size_training=1,
    sample_size_eval=10,
    grad_clip=5.,
    num_workers=2,
    device=torch.device('cuda:0')
    ):
    """
    训练VAE模型的函数。
    参数:
    - model: PyTorch模型
    - opts: 优化器集合OptCollection
    - training_data: 训练数据
    - dev_data: 开发/验证数据
    - batch_size: 批大小
    - num_epochs: 训练周期数
    - check_every: 每隔多少步检查一次开发集上的性能
    - sample_size_training: 训练时的样本大小
    - sample_size_eval: 评估时的样本大小
    - grad_clip: 梯度裁剪阈值
    - num_workers: 使用的工作进程数
    - device: 运行实验的设备
    返回:
    - 训练过程中计算的数量的日志（用于绘图）
    """
    # 创建训练和开发数据的数据加载器
    batcher = DataLoader(training_data, batch_size, shuffle=True, num_workers=num_workers, pin_memory=True)
    dev_batcher = DataLoader(dev_data, batch_size, num_workers=num_workers, pin_memory=True)

    # 初始化日志记录器和其他变量
    total_steps = num_epochs * len(batcher)
    log = defaultdict(list)

    # 训练循环
    step = 0
    # 评估模型在开发集上的性能
    model.eval()
    for k, v in assess(model, sample_size_eval, dev_batcher, device=device).items():
        log[f"dev.{k}"].append((step, v))

    # 使用tqdm显示进度条
    with tqdm(range(total_steps)) as bar:
        for epoch in range(num_epochs):
            for batch_x, batch_y in batcher:
                # 设置模型为训练模式
                model.train()
                # 零化梯度
                opts.zero_grad()

                # 计算损失字典
                loss_dict = model(
                    batch_x.to(device), 
                    sample_size=sample_size_training,
                )
                # 记录训练损失
                for metric, value in loss_dict.items():
                    log[f'training.{metric}'].append((step, value))

                # 反向传播
                loss_dict['loss'].backward()

                # 梯度裁剪
                nn.utils.clip_grad_norm_(
                    model.parameters(), 
                    grad_clip
                )    
                # 更新优化器
                opts.step()

                # 更新进度条
                bar_dict = OrderedDict()
                for metric, value in loss_dict.items():
                    bar_dict[f'training.{metric}'] = f"{loss_dict[metric]:.2f}"
                for metric in ['ELBO', 'D', 'R', 'L']:
                    bar_dict[f"dev.{metric}"] =  "{:.2f}".format(log[f"dev.{metric}"][-1][1])
                bar.set_postfix(bar_dict)
                bar.update()

                # 定期在开发集上评估模型
                if step % check_every == 0:
                    model.eval()
                    for k, v in assess(model, sample_size_eval, dev_batcher, device=device).items():
                        log[f"dev.{k}"].append((step, v))

                step += 1

    # 训练结束后，再次评估模型在开发集上的性能
    model.eval()
    for k, v in assess(model, sample_size_eval, dev_batcher, device=device).items():
        log[f"dev.{k}"].append((step, v))

    return log

# 用于检查样本的函数，例如检查VAE生成的样本。
def inspect_discrete_lvm(model, dl, device):
    for x, y in dl:    
        # 生成先验样本
        x_ = model.sample(16, 4, oversample=True).cpu().reshape(-1, 1, 64, 64)
        plt.figure(figsize=(12,6))
        plt.axis('off')
        plt.imshow(make_grid(x_, nrow=16).permute((1, 2, 0)))    
        plt.title("先验样本")
        plt.show()

        # 显示观测样本
        plt.figure(figsize=(12,6))
        plt.axis('off')
        plt.imshow(make_grid(x, nrow=16).permute((1, 2, 0)))    
        plt.title("观测")
        plt.show()

        # 生成条件样本
        x_ = model.cond_sample(x.to(device)).cpu().reshape(-1, 1, 64, 64)
        plt.figure(figsize=(12,6))
        plt.axis('off')
        plt.imshow(make_grid(x_, nrow=16).permute((1, 2, 0)))    
        plt.title("条件样本")
        plt.show()

        break

3.5.2 方差缩减技巧

以下是一些用于减少方差的实用策略，如果这是您首次接触这些概念，可以选择先跳过。

class CentredReward(VarianceReduction):
    """
    这个控制变量没有可训练的参数，
    它维护一个平均奖励的运行估计，并通过对奖励计算 reward - avg 来更新一批奖励。
    """

    def __init__(self, alpha=0.9):
        super().__init__()  # 调用父类的构造函数
        self._alpha = alpha  # 衰减系数
        self._r_mean = 0.  # 初始化平均奖励

    def forward(self, r, x=None, q=None, r_fn=None):
        """
        使奖励居中并更新平均值的运行估计。
        """        
        with torch.no_grad():  # 不计算梯度
            r_mean = torch.mean(r, dim=0)  # 计算奖励的均值
            r = r - self._r_mean  # 居中奖励
            self._r_mean = (1-self._alpha) * self._r_mean + self._alpha * r_mean.item()  # 更新平均奖励估计
        return r, torch.zeros_like(r)  # 返回居中后的奖励和零向量


class ScaledReward(VarianceReduction):
    """
    这个控制变量没有可训练的参数，
    它维护一个奖励的标准差的运行估计，并通过计算 reward / max(stddev, 1) 来更新一批奖励。
    """

    def __init__(self, alpha=0.9):
        super().__init__()
        self._alpha = alpha
        self._r_std = 1.0  # 初始化标准差

    def forward(self, r, x=None, q=None, r_fn=None):
        """
        通过运行估计的标准差来缩放奖励，并同时更新估计。
        """        
        with torch.no_grad():
            r_std = torch.std(r, dim=0)  # 计算奖励的标准差
            r = r / self._r_std  # 标准化信号
            self._r_std = (1-self._alpha) * self._r_std + self._alpha * r_std.item()  # 更新标准差估计
            self._r_std = np.maximum(self._r_std, 1.)  # 确保缩放因子至少为1
        return r, torch.zeros_like(r)


class SelfCritic(VarianceReduction):
    """
    这个控制变量没有可训练的参数，
    它通过计算 reward - reward' 来更新一批奖励，其中 reward' 是评估新的样本 z' ~ Z|X=x 时的 (log p(X=x|Z=z')).detach()。
    """

    def __init__(self):
        super().__init__()        

    def forward(self, r, x, q, r_fn):
        """
        标准化奖励并更新运行估计的均值/标准差。
        """
        with torch.no_grad():
            z = q.sample()  # 从分布中采样z
            r = r - r_fn(z, x)  # 更新奖励
        return r, torch.zeros_like(r)


class Baseline(VarianceReduction):
    """
    一个输入依赖的基线，实现为一个多层感知器（MLP）。
    通过均方误差调整可训练参数。
    """

    def __init__(self, num_inputs, hidden_size, p_drop=0.):
        super().__init__()
        self.baseline = nn.Sequential(
            FlattenImage(),  # 将图像展平
            nn.Dropout(p_drop),
            nn.Linear(num_inputs, hidden_size),
            nn.ReLU(),
            nn.Dropout(p_drop),
            nn.Linear(hidden_size, 1)  # 输出一个值
        )

    def forward(self, r, x, q=None, r_fn=None):
        """
        返回 r - baseline(x) 和基线的损失。
        """
        r_hat = self.baseline(x)  # 计算基线预测
        r_hat = r_hat.squeeze(-1)  # 压缩维度
        loss = (r - r_hat)**2  # 计算损失
        return r - r_hat.detach(), loss  # 返回更新后的奖励和损失


class CVChain(VarianceReduction):
    """
    控制变量链，可以串联多个控制变量。
    """

    def __init__(self, *args):
        super().__init__()
        # 添加模块到当前类
        if len(args) == 1 and isinstance(args[0], OrderedDict):
            for key, module in args[0].items():
                self.add_module(key, module)
        else:
            for idx, module in enumerate(args):
                self.add_module(str(idx), module)
    
    def forward(self, r, x, q, r_fn):         
        loss = 0  # 初始化损失
        for cv in self._modules.values():  # 遍历所有控制变量
            r, l = cv(r, x=x, q=q, r_fn=r_fn)  # 更新奖励和损失
            loss = loss + l  # 累加损失
        return r, loss  # 返回更新后的奖励和总损失

3.5.3.实验

# 设置随机种子以确保结果的可复现性（虽然这里没有直接显示seed_all()的具体实现）  
seed_all()  
  
# 创建一个NVIL（神经变分推断和学习）模型  
# NVIL模型由联合分布（JointDistribution）、推理模型（InferenceModel）和方差缩减策略（VarianceReduction）组成  
model = NVIL(  
    # 联合分布：由BernoulliPriorNet（先验网络）和BinarizedImageModel（二值化图像模型）组成  
    JointDistribution(  
        # 先验网络，用于生成10维的潜在变量  
        BernoulliPriorNet(10),  
        # 图像模型，它接收10维的潜在变量作为输入，并预测与给定图像尺寸相对应的图像分布  
        BinarizedImageModel(  
            num_channels=img_shape[0],  # 图像通道数  
            width=img_shape[1],         # 图像宽度  
            height=img_shape[2],        # 图像高度  
            latent_size=10,             # 潜在变量的大小  
            p_drop=0.1                  # dropout的概率  
        )  
    ),  
    # 推理模型，用于近似后验分布  
    InferenceModel(  
        latent_size=10,                # 潜在变量的大小  
        num_channels=img_shape[0],     # 图像通道数  
        width=img_shape[1],            # 图像宽度  
        height=img_shape[2],           # 图像高度  
        cpd_net_type=BernoulliCPDNet   # 控制变分分布的网络类型  
    ),  
    # 方差缩减策略：这里暂时没有使用任何方差缩减策略  
    VarianceReduction(), # 不使用方差缩减  
  
    # 在NVIL论文中，他们使用了以下方差缩减策略：  
    # CVChain(  
    #     CentredReward(),        # 中心化奖励  
    #     #Baseline(np.prod(img_shape), 512), # 如果你使用训练过的基线，可以这样使用  
    #     #ScaledReward()         # 缩放奖励  
    # )  
).to(my_device)  # 将模型移动到指定的设备（如GPU）  
  
# 创建优化器集合  
# 对于生成模型的参数和推理模型的参数，我们分别使用RMSprop优化器  
opts = OptCollection(  
    opt.RMSprop(model.gen_params(), lr=5e-4, weight_decay=1e-6),  # 生成模型的参数  
    opt.RMSprop(model.inf_params(), lr=1e-4),                    # 推理模型的参数  
  
    # 如果你使用的基线具有可训练的参数，你需要为这些参数也设置一个优化器  
    # opt.RMSprop(model.cv_params(), lr=1e-4, weight_decay=1e-6) # 你需要这个如果你的基线有可训练的参数  
)  
  
# 显示模型的结构或信息（这取决于model对象的实现）  
model

# 初始化日志记录器，用于记录训练过程中的各种数据。
log = train_vae(
    # 传入要训练的模型。
    model=model,
    # 传入优化器集合，用于更新模型参数。
    opts=opts,
    # 传入训练数据集。
    training_data=train_ds, 
    # 传入验证数据集，用于评估模型性能。
    dev_data=val_ds,
    # 设置批大小，即每次迭代中使用的样本数量。
    batch_size=256, 
    # 设置训练周期数，更多的周期可能有助于模型更好地收敛。
    num_epochs=3,
    # 设置检查频率，即每隔多少步在验证集上评估一次模型。
    check_every=100,
    # 设置训练时使用的样本大小。
    sample_size_training=1,
    # 设置评估时使用的样本大小。
    sample_size_eval=1,
    # 设置梯度裁剪的阈值，用于防止梯度爆炸问题。
    grad_clip=5.,
    # 设置运行模型的设备，例如GPU或CPU。
    device=my_device
)

# 获取日志记录器中所有的键名。
log_keys = log.keys()

# 根据日志中是否包含'training.cv_loss'键，创建一个包含3个或4个子图的图形。
# figsize参数设置图形的大小。
fig, axs = plt.subplots(1, 3 + int('training.cv_loss' in log), sharex=True, sharey=False, figsize=(12, 3))

# 绘制训练过程中的ELBO值。
# 取日志中'training.ELBO'键对应的数据，绘制其第一列（步骤）和第二列（ELBO值）。
_ = axs[0].plot(np.array(log['training.ELBO'])[:, 0], np.array(log['training.ELBO'])[:, 1])
# 设置y轴标签为"training ELBO"。
_ = axs[0].set_ylabel("training ELBO")
# 设置x轴标签为"steps"。
_ = axs[0].set_xlabel("steps")

# 绘制训练过程中的D值。
_ = axs[1].plot(np.array(log['training.D'])[:, 0], np.array(log['training.D'])[:, 1])
_ = axs[1].set_ylabel("training D")
_ = axs[1].set_xlabel("steps")

# 绘制训练过程中的R值。
_ = axs[2].plot(np.array(log['training.R'])[:, 0], np.array(log['training.R'])[:, 1])
_ = axs[2].set_ylabel("training R")
_ = axs[2].set_xlabel("steps")

# 如果日志中包含'training.cv_loss'键，则在第四个子图中绘制控制变量链的损失值。
if 'training.cv_loss' in log:
    _ = axs[3].plot(np.array(log['training.cv_loss'])[:, 0], np.array(log['training.cv_loss'])[:, 1])
    _ = axs[3].set_ylabel("cv loss")
    _ = axs[3].set_xlabel("steps")

# 使用tight_layout调整子图布局，h_pad和w_pad参数分别设置水平和垂直间距。
fig.tight_layout(h_pad=1.2, w_pad=1.2)

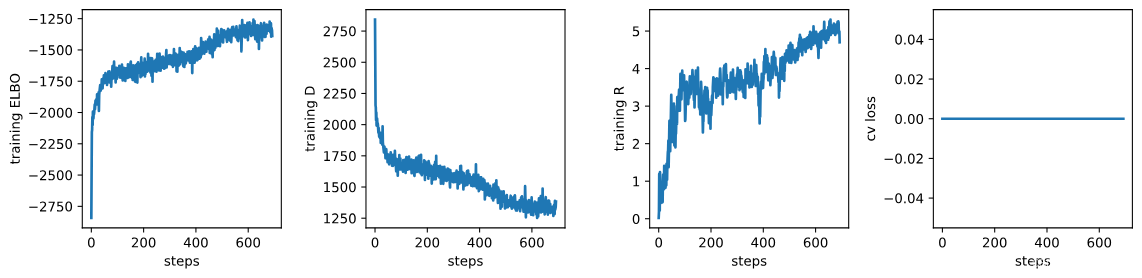
在这里插入图片描述

# 创建一个图形和4个共享x轴但不共享y轴的子图。
# figsize参数设置图形的大小。
fig, axs = plt.subplots(1, 4, sharex=True, sharey=False, figsize=(12, 3))

# 绘制开发集上的ELBO值。
# 取日志中'dev.ELBO'键对应的数据，绘制其第一列（步骤）和第二列（ELBO值）。
_ = axs[0].plot(np.array(log['dev.ELBO'])[:, 0], np.array(log['dev.ELBO'])[:, 1])
# 设置第一个子图的y轴标签为"dev ELBO"。
_ = axs[0].set_ylabel("dev ELBO")
# 设置第一个子图的x轴标签为"steps"。
_ = axs[0].set_xlabel("steps")

# 绘制开发集上的D值。
_ = axs[1].plot(np.array(log['dev.D'])[:, 0], np.array(log['dev.D'])[:, 1])
_ = axs[1].set_ylabel("dev D")
_ = axs[1].set_xlabel("steps")

# 绘制开发集上的R值。
_ = axs[2].plot(np.array(log['dev.R'])[:, 0], np.array(log['dev.R'])[:, 1])
_ = axs[2].set_ylabel("dev R")
_ = axs[2].set_xlabel("steps")

# 绘制开发集上的L值。
_ = axs[3].plot(np.array(log['dev.L'])[:, 0], np.array(log['dev.L'])[:, 1])
_ = axs[3].set_ylabel("dev L")
_ = axs[3].set_xlabel("steps")

# 使用tight_layout调整子图布局，h_pad和w_pad参数分别设置水平和垂直间距。
fig.tight_layout(h_pad=1.2, w_pad=1.2)

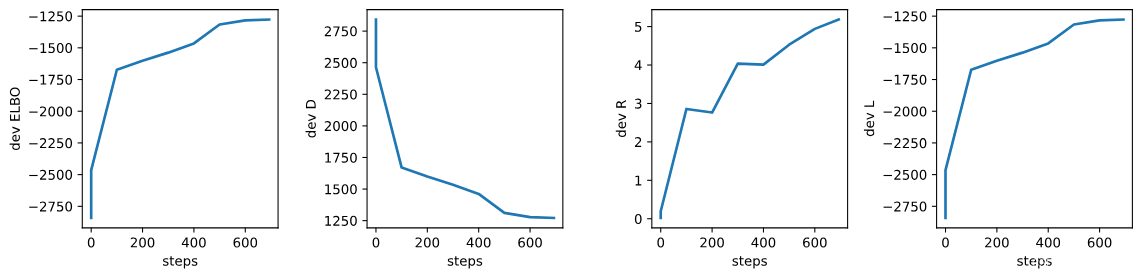
在这里插入图片描述

# 调用 inspect_discrete_lvm 函数来检查或可视化离散潜在变量模型  
# 参数：  
#   model: 模型对象，即已经定义好的离散潜在变量模型  
#   DataLoader(val_ds, 64, num_workers=2, pin_memory=True): 用于加载验证数据集的数据加载器  
#     val_ds: 验证数据集  
#     64: 批处理大小（每批加载64个样本）  
#     num_workers=2: 使用2个工作线程来加载数据  
#     pin_memory=True: 如果在GPU上运行，将数据加载到固定内存中以提高效率  
#   my_device: 设备对象，指定模型应在哪个设备上运行（如 'cuda:0' 表示第一个GPU）  
inspect_discrete_lvm(model, DataLoader(val_ds, 64, num_workers=2, pin_memory=True), my_device)

在这里插入图片描述

4. 总结和展望

4.1 总结

本文深入探讨了使用深度学习进行概率建模的方法，尤其集中在变分自编码器（VAE）和神经变分推断（NVIL）的应用上。从预备知识到模型建立，再到训练与评估，文章提供了一套完整的流程。

预备知识：涵盖了PyTorch库的使用、数据预处理、随机种子设置等基础操作。
模型建立：介绍了如何构建具有离散潜在变量的模型，包括先验网络、条件概率分布网络，以及联合概率分布模型。
训练流程：讨论了最大似然估计和变分推断两种方法，以及如何使用优化器更新模型参数。
评估与可视化：提供了评估模型性能的方法，并通过Matplotlib对结果进行了可视化展示。

4.2 展望

尽管本文所讨论的方法在理论上和实践上都具有重要意义，但仍有一些潜在的研究方向和应用场景值得进一步探索：

模型改进：当前的模型可能在表达能力和泛化性能上有所限制，未来的工作可以探索更复杂的网络结构或引入新的归纳偏置。
算法优化：训练过程可能需要更高效的算法来加速收敛或提高参数估计的准确性，例如通过改进优化器或引入先进的正则化技术。
应用拓展：本文的方法可以应用于更广泛的领域，如自然语言处理、计算机视觉等，探索这些方法在不同领域的应用将是一个有趣的研究方向。
方差缩减技术：本文提到了一些减少方差的技术，但这一领域仍然有待深入研究，以发现更有效的策略来提高训练过程的稳定性和效率。
可扩展性研究：随着数据规模的增长，研究如何扩展模型以处理大规模数据集也是一个重要的方向。

4.2.1.提高方向

你可以尝试使用连续的输出分布和CNN编码器/解码器。
尝试打开和关闭基线。
使用变分推断（VI），你应该能够使用更大的 $K$ 值的混合模型，甚至可以与CNN解码器一起使用。
你可以改变数据集（例如，使用SVHN，其图像是彩色的，因此你将使用3个通道）。
你可以尝试（半）监督潜在编码（因为这些数据集提供了一定程度的监督）。为此，你可以使用基于模型组件的对数似然旁侧损失，该模型组件预测给定潜在编码的图像类别的概率质量函数 $p_{Y|Z}(y|z, \phi)$ 。

参考文献

本文的撰写参考了以下文献和资源，为读者提供了进一步阅读和研究的起点：

Kingma, D. P., & Welling, M. (2013). Auto-Encoding Variational Bayes. In ICLR.
Rezende, D. J., & Mohamed, S. (2014). Variational Inference with Normalizing Flows. In ICML.
Goodfellow, I., et al. (2014). Generative Adversarial Networks. In NIPS.
Salimans, T., et al. (2015). Markov Chain Monte Carlo without Likelihoods. In ICML.
Schulman, J., et al. (2015). Gradient Estimation Using Stochastic Computation Graphs. In ICLR.