目录
前言
基本原理
对撞指针
快慢指针
移动零
算法思路
算法步骤
代码实现
算法分析
复写零
算法思路
算法步骤
代码实现
快乐数
算法思路
算法步骤
代码实现
盛最多水的容器
编辑算法思路
代码实现
前言
双指针是一种在数组或链表等线性数据结构中高效解决问题的算法思想,适用于查找、排序、去重等场景。
基本原理
双指针的原理主要是利用两个指针(或索引)从不同起点出发,按照某种规则移动,直至满足某种终止条件。
常见的双指针有两种形式:1、对撞指针,2、快慢指针
本篇主要讲解快慢指针。
对撞指针
一般用于顺序结构中,也称为左右指针。
思路:
- 对撞指针从两端向中间移动。一个指针从最左端开始,另一个从最右端开始,然后逐渐向中间逼近
- 对撞指针的终止条件一般是两个指针相遇或者错开(也可能在循环内部找到结果直接跳出循环),即:
left==right(两个指针指向同一个位置)
left>right(两个指针错开)
快慢指针
⼜称为⻳兔赛跑算法,其基本思想就是使⽤两个移动速度不同的指针在数组或链表等序列 结构上移动。对于处理环形链表或者数组非常有用。
不单单是环形链表或者是数组,如果我们要研究的问题出现循环往复的情况时,均可考虑使⽤快 慢指针的思想。
快慢指针的实现⽅式有很多种,最常⽤的⼀种就是: 在⼀次循环中,每次让慢的指针向后移动⼀位,⽽快的指针往后移动两位,实现⼀快⼀慢。
移动零
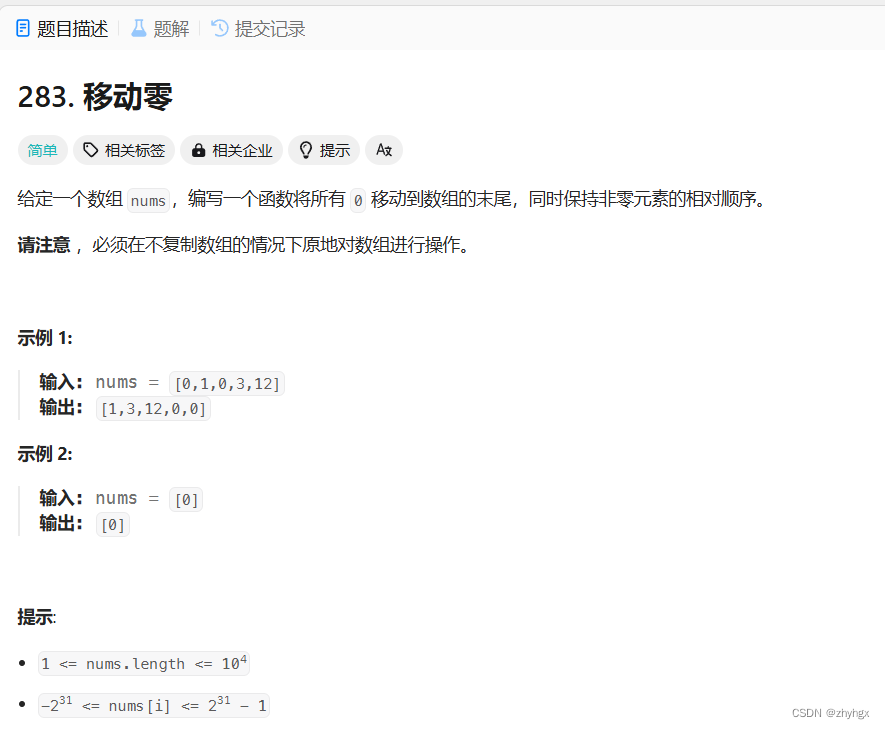
算法思路
在本道题中,我们可以定义一个right来扫描数组,定义一个left,负责当right遇到非0数时,与left进行交换。当right遍历完数组后,也就将数组按照其相对顺序,把非0数移动到left之前,把所有0移动到left之后。
算法步骤
-
定义双指针left,right
-
让right先走
-
当right遇到非0数,与left进行交换,再让left++
-
当right遍历完数组,移动结束
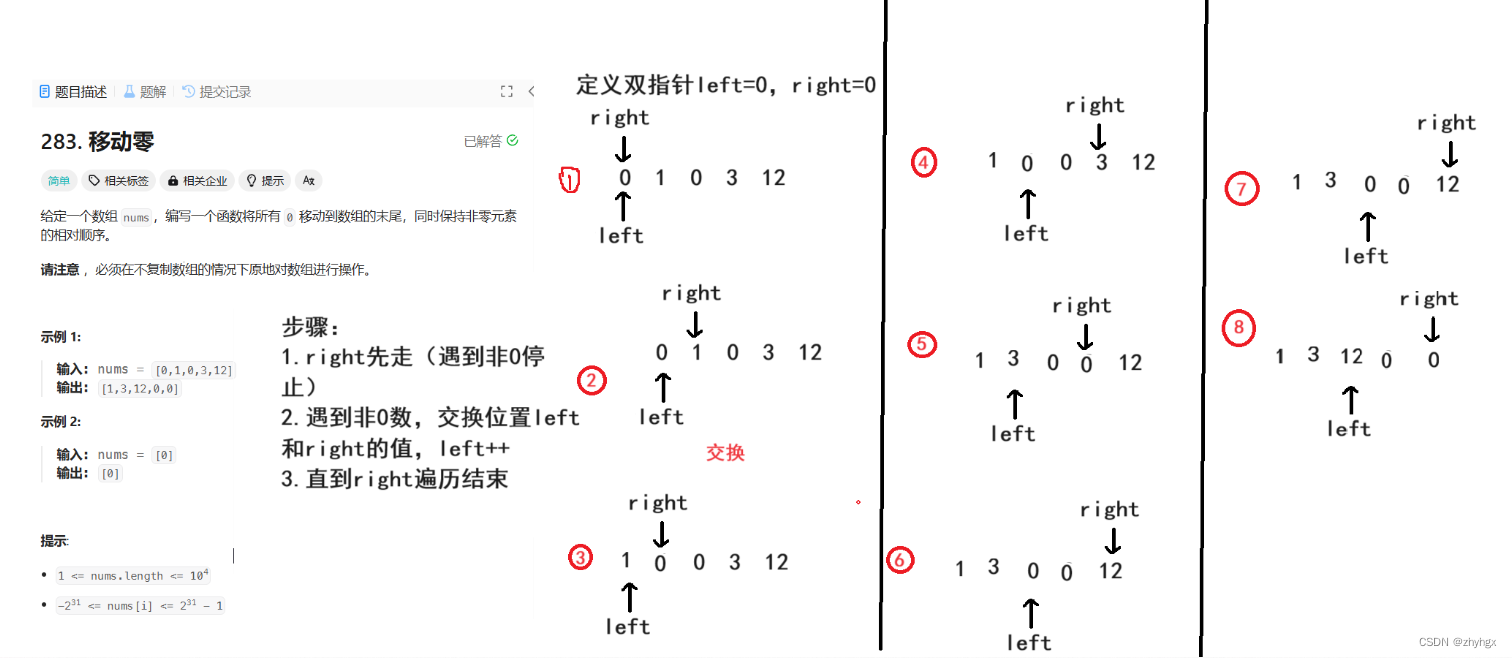
代码实现
/**
* 交换数组中两个位置的元素。
*
* @param nums 输入的整数数组。
* @param i 第一个位置的索引。
* @param j 第二个位置的索引。
*/
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
/**
* 将数组中的所有零移动到末尾,同时保持非零元素的相对顺序不变。
*
* @param nums 输入的整数数组。
*/
public void moveZeroes(int[] nums) {
// 如果数组为空,则无需进行任何操作
if (nums.length == 0) {
return;
}
int left = 0;
int right = 0;
// 遍历数组,将非零元素依次交换到数组的左侧
while (right < nums.length) {
if (nums[right] != 0) {
// 交换当前非零元素到左侧
swap(nums, left, right);
// 左指针向右移动,准备交换下一个非零元素
left++;
}
// 右指针继续向右移动,扫描下一个元素
right++;
}
}算法分析
时间复杂度为O(N),只遍历了一遍数组,空间复杂度O(1),只用到了常数个变量。
复写零
算法思路
利用双指针
- cur指针:初始化为0,负责从数组的起始位置遍历数组,用于查找0元素并对新数组进行布局,记录新数组最后一个元素
- dest指针:初始化为-1,当cur在遍历时,遇到0走两步,非0走1步,当dest走到数组末尾时,此时就能确定cur要复写的起始位置。当确定完cur要开始复写的位置,从后往前进行复写。
算法步骤
- 复写预备:首先通过cur对数组进行遍历,在dest越界的情况下,dest能到的位置为数组的最后一个元素位置,此时停止遍历。
- 处理dest越界情况:如果dest在数组倒数第二个元素位置,而此时cur下标的值为0,那么dest就会越界。由于数组已满,只能将数组最后一个元素复制为0,并相应调整cur和dest的位置(cur--,dest-=2)
- 从后往前复制:从dest出发,判断cur的值是否为0,为0,dest位置先复制为0,再dest--,再复制为0,再dest--,若cur位置的值不为0,则让cur位置的值给dest位置,dest--,当dest<0时,复制结束
代码实现
/**
* 复制数组中的零。
* 将数组arr中的零复制一倍,并尽可能地填入数组中,可能会覆盖原数组的部分元素。
* 如果复制零后,数组末尾无法再放置一个零,则将最后一个非零元素替换为零。
* 此方法直接在原数组上进行操作,不返回新数组。
*
* @param arr 原数组,将在此数组上进行操作。
*/
public void duplicateZeros(int[] arr) {
// 获取数组长度
int len = arr.length;
// 初始化当前索引cur和目标索引dest
int cur = 0;
int dest = -1; // dest从-1开始,因为下一个要填入的位置是dest+1
// 遍历数组,计算每个非零元素和零元素应该填入的位置
int dest=-1;//dest从-1开始
for (; cur < len; cur++) {
// 如果当前元素不为零,目标索引移动一步
// 如果当前元素为零,目标索引移动两步
// 判断cur是否为0,若为0,dest移动2步,反之,移动1步
if (arr[cur] != 0) {
dest++;
} else {
dest += 2;
}
// 如果目标索引超出或等于数组长度减一,则无法再放置更多元素,结束循环
// 判断dest是否到到数组末尾,若到达末尾,则说明不需要移动,直接返回
if (dest >= len - 1) {
break;
}
}
// 检查是否需要将最后一个元素替换为零
if (dest == len) {
arr[len - 1] = 0;
cur--;
dest -= 2;
}
// 从后向前复制元素,实现零的复制
// 进行复写
while (dest >= 0) {
// 如果当前元素为零,则在目标位置复制两个零
if (arr[cur] == 0) {
arr[dest--] = 0;
arr[dest--] = 0;
} else {
// 如果当前元素不为零,则复制到目标位置
arr[dest--] = arr[cur];
}
cur--;
}
}
时间复杂度为O(N),空间复杂度为O(1).
快乐数
算法思路
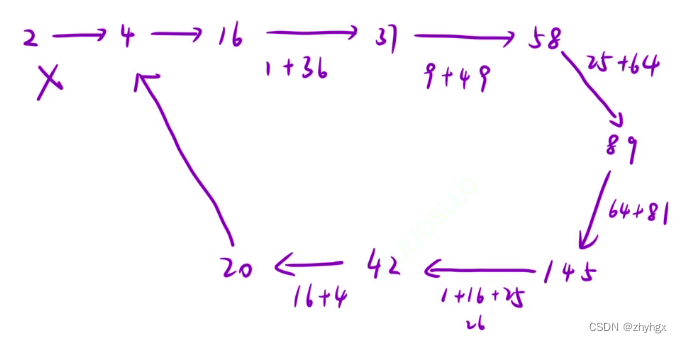
快乐数的原理于链表是否成环相似。利用快慢指针即可解决。 根据上述的题⽬分析,我们可以知道,当重复执⾏ x 的时候,数据会陷⼊到⼀个「循环」之中。【快慢指针】有⼀个特性,就是在⼀个圆圈中,快指针总是会追上慢指针的,也就是说他们总会相遇在⼀个位置上。如果相遇位置的值是 1 ,那么这个数⼀定是快乐数;如果相遇位置不是1的话,那么就不是快乐数。
算法步骤
- isSum:主要用来求⼀个数 n 每个位置上的数字的平⽅和。
- isHappy:用来判断一个数是不是快乐数
- 在isHappy中,首先定义两个指针:快指针fast和慢指针slow,slow初始化为n,fast初始化为isSum(n),即先进行一次计算。
- 循环判断:条件为(slow!=fast),在while循环中,slow每次调用一次isSum进行计算,而fast则每次调用两次isSum进行计算。当slow和fast的值相等时,则说明成环。
- 返回:当循环结束后,返回slow==1,即判断n是不是快乐数。
代码实现
/**
* 计算一个数字的各位平方和。
*
* @param n 输入的整数
* @return 各位数字的平方和
*/
public int isSum(int n){
int sum=0;
while(n!=0){
sum+=Math.pow(n%10,2);
n=n/10;
}
return sum;
}
/**
* 判断一个数字是否为“快乐数”。
* “快乐数”是指在一系列操作后,最终得到1的数。
* 操作是将数字的各位数的平方相加,然后重复这个过程。
*
* @param n 输入的整数,用于判断是否为快乐数
* @return 如果n是快乐数,返回true;否则返回false
*/
public boolean isHappy(int n) {
int slow=n;
int fast=isSum(n);
while(slow!=fast){
slow=isSum(slow);
fast=isSum(isSum(fast));//快指针走两步,慢指针走一步
}
return slow==1;
}代码时间复杂度为O(logN),空间复杂度为O(1).
盛最多水的容器
 算法思路
算法思路
- 设两个指针 left , right 分别指向容器的左右两个端点,此时容器的容积 : v = (right - left) * min( height[right], height[left]) 容器的左边界为 height[left] ,右边界为 height[right] 。
- 为了⽅便叙述,我们假设「左边边界」⼩于「右边边界」。
- 如果此时我们固定⼀个边界,改变另⼀个边界,⽔的容积会有如下变化形式:
- 容器的宽度⼀定变⼩。
- 由于左边界较⼩,决定了⽔的⾼度。如果改变左边界,新的⽔⾯⾼度不确定,但是⼀定不会超右边的柱⼦⾼度,因此容器的容积可能会增⼤。
- 如果改变右边界,⽆论右边界移动到哪⾥,新的⽔⾯的⾼度⼀定不会超过左边界,也就是不会过 现在的⽔⾯⾼度,但是由于容器的宽度减⼩,因此容器的容积⼀定会变⼩的。
由此可⻅,左边界和其余边界的组合情况都可以舍去。所以我们可以 left++ 跳过这个边界,继续去判断下⼀个左右边界。
当我们不断重复上述过程,每次都可以舍去⼤量不必要的枚举过程,直到 left 与 right 相遇。期间产⽣的所有的容积⾥⾯的最⼤值,就是最终答案.
代码实现
/**
* 计算两个非递减序列中形成的最大矩形区域的面积。
* 该方法使用双指针技术来找到最大的矩形面积,避免了对每个可能的矩形进行遍历,提高了效率。
*
* @param height 一个整数数组,表示每个位置的高度。
* @return 返回最大的矩形面积。
*/
public int maxArea(int[] height) {
// 初始化左指针、面积为0,和右指针
int left = 0;
int V = 0;
int right = height.length - 1;
// 当左指针小于右指针时,进行循环
while (left < right) {
// 计算当前形成的矩形的最小高度
int h = Math.min(height[left], height[right]);
// 计算当前形成的矩形的宽度
int len = right - left;
// 更新当前的最大面积
V = Math.max(V, h * len);
// 根据左指针和右指针指向的高度,移动指针
if (height[left] < height[right]) {
left++;
} else {
right--;
}
}
// 返回最大面积
return V;
}该算法的时间复杂度为O(N)只遍历了一遍数组,空间复杂度为O(1),只使用了常数个变量.
双指针上篇就先到这~
若有不足,欢迎指正~