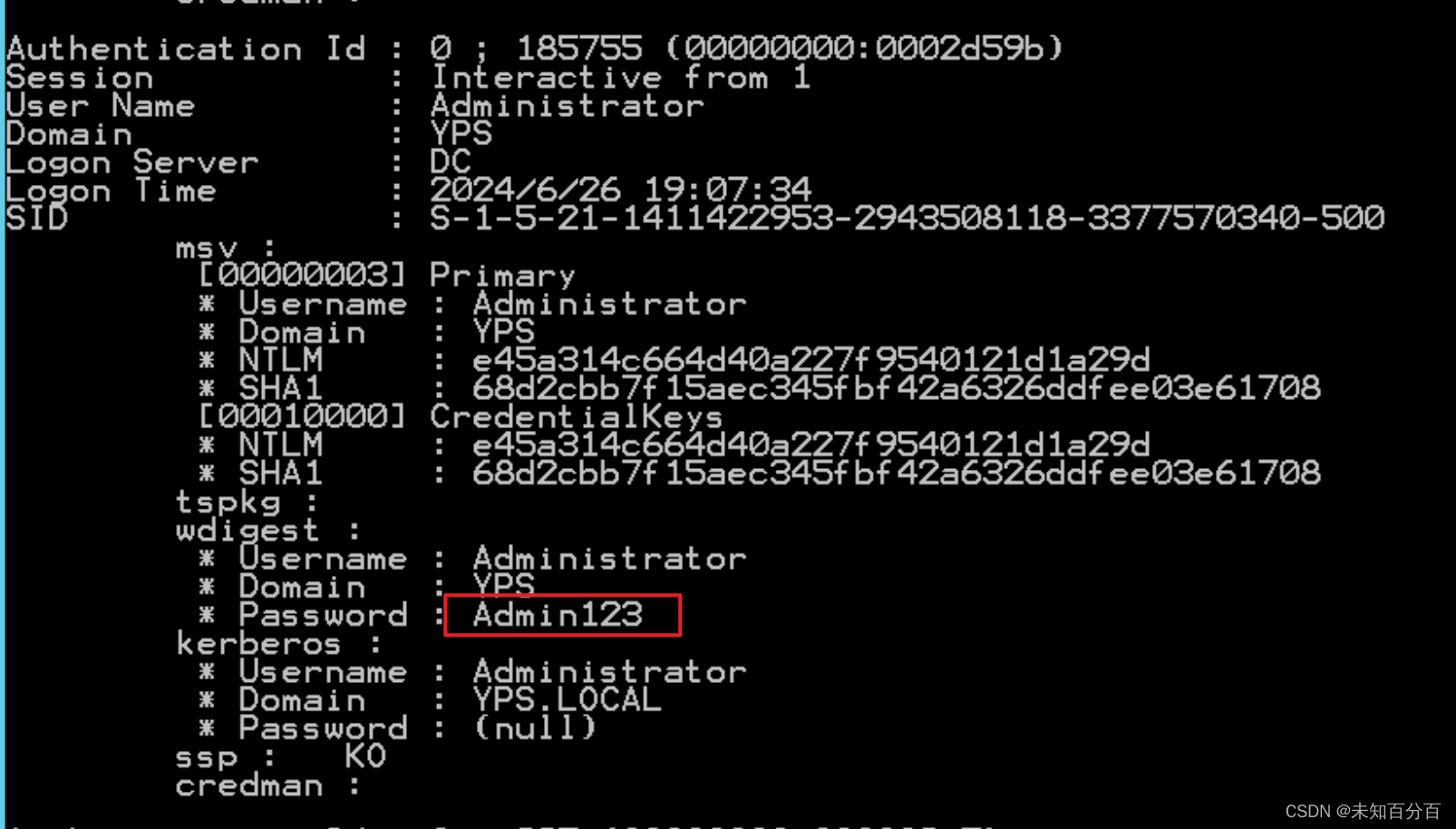
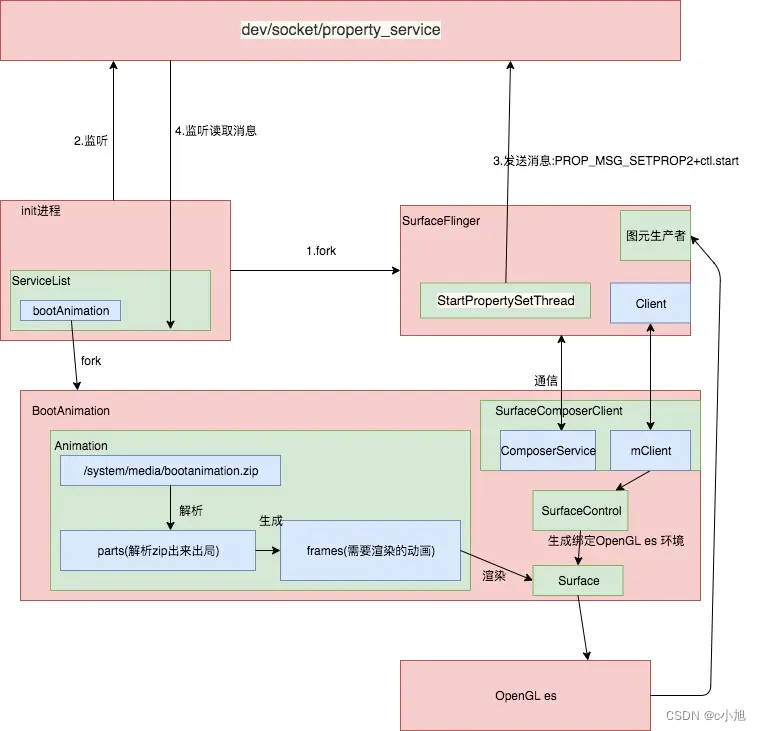
分析

步骤之间有何关联？

思考的逻辑：

第一步得到4，b=a%10;即可

第二步得到3，但需要先得到123，所以要除10，即c=(a/10) %10;

第三步得到2，但需要先得到12 ，所以要除100，即d=( a/100 ) %10;

第四步得到1，但需要先得到1 ，所以要除1000 ，即f=(a/1000 ) %10;

似乎能得出结论：

每一次取个位数前，都需要先得到除了个位数以外其他那些数，而从步骤2开始，那些数实际上除过一次10了，下次再除一次10就行了。

能否改进一下，把上次除10的结果利用上？

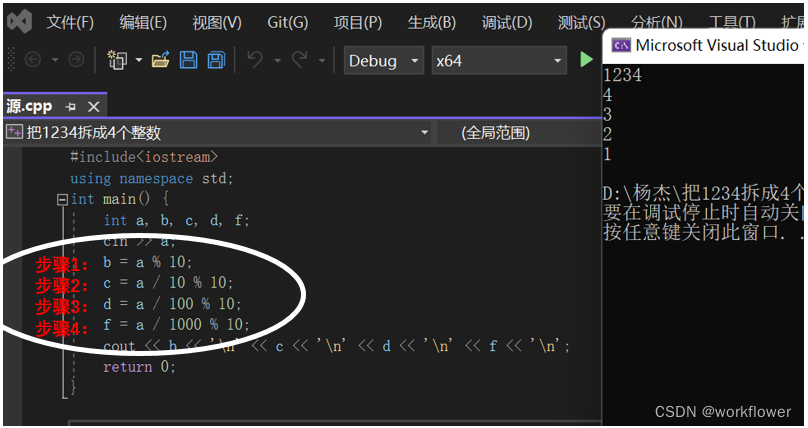
沿着这个思路再改进一下：

步骤1改成：

b=a%10;

步骤2改成：

t=a /10 ;

c= t %10;   

步骤3改成：

t=t /10 ;

d= t %10;   

步骤4改成：

t=t /10 ;

f= t %10;   

// 这种改进，看着代码更长了，所谓的“利用上次结果”其实只是除10，从计算机运行效率看，除10和除100效率上没差别，似乎并没有改进，反而还要多执行很多语句。

// 这个ppt是一个思考过程的整理，希望大家都反思一下自己的思路，而且所谓“上次计算结果”、“除10”，这些并不是因为觉得“(a/1000 ) %10”和“(a/100 ) %10”它们长得相似通过数学思维推导而来，而应该是从功能实现角度考虑哪些是可重用的功能。以后还会看到各种各样的例子，并非都有这样一种公式可“推导”。

也许这个例子不恰当，如果所谓的“上次结果”是一大堆代码，这样的改进就有意义了，初学第二节课，还不能用复杂例子说明这个问题。还有，如果仍然觉得这种改进没必要，那请看下一页的演变。

#include <iostream>
using namespace std;
int main( )
{
	int a,t;
	cin>>a;
	t=a; 
	for(int i=0;i<4;i++){
		cout <<  t%10  << "\t";
		t=t/10;
	}
	return 0;
}

//之前抽取出公共的操作“t=t /10 ; ” ，就可以使用循环啦。

不过这个程序还有瑕疵，它结果输出是反的，输入1234，输出4321，还需要再做点工作，比如分离每位数从千位到个位的顺序，或者引入数组等等，讨论先到此为止。