1.什么是机器学习?
机器学习是人工智能(AI)的一个分支,它使计算机系统能够从经验中学习并根据这些学习的数据做出决策或预测,而无需进行明确的编程。简而言之,机器学习涉及算法和统计模型的使用,使计算机能够执行特定任务,通过分析和学习输入数据来提高性能。
主要类型
机器学习通常可以分为以下几种类型:
-
监督学习:这是最常见的类型,其中模型通过已标记的训练数据学习。算法试图学习输入数据到输出数据的映射函数。例如,基于一系列的邮件数据(输入),机器学习模型可以学习区分哪些是垃圾邮件,哪些不是(输出)。
-
无监督学习:在这种类型中,算法被用来分析和聚类未标记的数据。由于输入数据没有标签,模型试图自己找出数据的结构。这常用于市场细分、社群检测等场景。
-
强化学习:在强化学习中,算法通过试错法在特定环境中作出决策,并根据这些决策的结果来学习和调整策略。这是学习优化策略的一种方式,广泛用于游戏、机器人导航等领域。
-
半监督学习:这种方法结合了监督学习和无监督学习。使用部分标记的数据训练模型,这种类型的学习用于当获取完全标记的数据成本过高或不可行时。
-
自监督学习:这是一种特殊类型的无监督学习,其中模型通过自我生成的标签从数据中学习。
关键技术和算法
-
神经网络:深度学习的核心技术,模拟人脑的神经元网络来处理复杂的数据结构。
-
决策树:通过构造决策树来进行分类和回归。
-
支持向量机(SVM):用于分类和回归的强大方法,它通过找到最佳的决策边界来区分不同的类别。
-
聚类算法:如 K-means、层次聚类等,用于将数据集中的样本分组。
-
回归分析:包括线性回归和逻辑回归,用于预测数值型或分类型输出。
应用领域
机器学习已经被广泛应用于多个领域,包括但不限于:
-
金融行业:用于信用评分、股市预测、欺诈检测等。
-
医疗领域:用于疾病诊断、医学图像分析、药物发现等。
-
自动驾驶汽车:通过机器学习进行环境感知、决策制定。
-
推荐系统:在电商、流媒体服务等平台上个性化推荐内容或产品。
-
自然语言处理:包括语音识别、机器翻译、情感分析等。
2.机器学习案例
计算给定数据集的香农熵(Shannon entropy)。香农熵是信息论中用来衡量信息的不确定性或混乱度的指标,通常用于分类任务中评估数据集的纯净度。
首先定义一个计算数据集香农熵的函数。
# 计算给定数据的香农熵
from math import log # 用于计算对数函数
def calShannoEnt(dataSet): # dataSet 参数是一个列表,其中每个元素也是一个列表,表示数据集中的一个实例
numEntries=len(dataSet) # 计算机数据集中的实例总数,也就是矩阵的函数
labelCounts={} # 创建一个空字典用来计数数据集中每个类标签的出现次数
for featVec in dataSet: #循环遍历数据集中的每个实例(列表)
currentLabel=featVec[-1] # 获取每个实例的最后一个元素作为标签(类别)
if currentLabel not in labelCounts.keys(): # 检查当前标签是否已经在 labelCounts 字典的键中,如果不在,则将其添加
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1 # 增加当前标签的计数
shannoEnt=0.0 # 香农熵的初始值设为0
for key in labelCounts: # 遍历字典中的每个键
prob=float(labelCounts[key])/numEntries # 计算当前标签的概率,即该标签出现的次数除以总实例数
shannoEnt -=prob*log(prob,2) #根据香农熵的定义,对每个类别标签的概率进行对数运算,并累加到香农熵中
return shannoEnt
创建一个简单的数据集:
# 创建一个简单的数据集
def createDataSet():
dataSet=[[1,1,'yes'],
[1,1,'yes'],
[1,0,'no'],
[0,1,'no'],
[0,1,'no']]
labels=['no surfacing','flippers'] # 列表包含两个字符串,分别代表数据集中各个特征的名称,这些名称对应于dataSet中每个实例的前两个元素
return dataSet,labels # 函数返回两个值,一个是数据集 dataSet,另一个是对应的特征标签列表 labels
myData,label=createDataSet()
myData
# 输出:
'''
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
'''
计算香农熵:
calShannoEnt(myData)
# 输出:
'''
0.9709505944546686
'''
尝试增加数据中的类别:
# 添加更多的分类,则熵值越高,混合的数据越多
myData[0][-1]='maybe' # 给第一行最后一个数据赋值
myData
# 输出:
'''
[[1, 1, 'maybe'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
'''
再次计算香农熵,会比之前的值大:
calShannoEnt(myData)
# 输出:
'''
1.3709505944546687
'''
根据数据集中的某个特定特征划分数据集:
# 按照给定特征换分数据集
'''
函数接受三个参数:
dataSet:要被划分的数据集,是一个列表的列表,其中每个内部列表代表数据集中的一个样本
axis:一个整数,指定要检查的特征的索引,这个索引决定了在每个样本中哪一个元素将被用来进行比较
value:与 axis 参数指定的特征进行比较的值,函数将基于此值来划分数据集
'''
def splitDataSet(dataSet,axis,value):
retDataSet=[] # 创建一个空列表,用来存储符合条件(特征值等于给定值 value)的样本,但去除了用于划分的特征
for featVec in dataSet: # 循环遍历数据集中的每一个样本
if featVec[axis]==value: # 检查当前样本的第axis个特征是否等于给定的value
reducedFeatVec=featVec[:axis] # 取当前样本从开始到第axis元素之前的部分,不包括axis索引处的元素
reducedFeatVec.extend(featVec[axis+1:]) # 将当前样本从axis+1索引到末尾的部分扩展到reducedFeatVec中
retDataSet.append(reducedFeatVec) # 将处理过的新样本添加到返回的数据集列表
return retDataSet
splitDataSet(myData,0,1) # 如果0索引处的数据等于1,则将该实例的数据位于索引0+1至结尾的数据获取
# 输出:
'''
[[1, 'maybe'], [1, 'yes'], [0, 'no']]
'''
尝试不同的函数参数设置:
splitDataSet(myData,0,0) # # 如果0索引处的数据等于0,则将该实例的数据位于索引0+1至结尾的数据获取
# 输出:
'''
[[1, 'no'], [1, 'no']]
'''
数据划分函数的目的是在给定的数据集中找到最佳的划分特征。该函数是决策树算法中的一个核心步骤,用于选择一个特征,使得按照这个特征划分数据后,信息增益最大,即数据的纯度提高最多。
# 选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
numFeatures=len(dataSet[0])-1 # 计算每个样本中的特征数量。减1是因为数据集中的最后一个元素被假定为类标签
baseEntropy=calShannoEnt(dataSet) # 计算整个数据集的初始熵,这是决策前数据的不确定性度量
bestInfoGain=0.0 # 初始化最大信息增益为0
bestFeature=-1 # 初始化最佳特征的索引为-1,表示还未找到
for i in range(numFeatures): #对数据集中的每个特征进行循环
featList=[example[i] for example in dataSet] # 提取当前特征i的所有值
uniqueVals=set(featList) # 获取当前特征的所有唯一值(因为set容器是集合,不允许有重复元素),这些值将用于分割数据集
newEntropy=0.0 # 初始化新的熵为0
for value in uniqueVals: # 循环遍历每个唯一值
subDataSet=splitDataSet(dataSet,i,value) # 根据当前特征i和特征值value划分数据集
prob=len(subDataSet)/float(len(dataSet)) # 计算划分出的子数据集在原数据集中的比例
newEntropy+=prob*calShannoEnt(subDataSet) # 计算加权熵,即当前特征值对应的子数据集的熵乘以其在总数据集中的比例,并累加
infoGain=baseEntropy-newEntropy # 计算信息增益,即初始熵减去划分后的熵
if(infoGain>bestInfoGain): # 如果当前特征的信息增益大于之前的最大信息增益,则更新最佳特征和最大信息增益
bestFeature=i
bestInfoGain=infoGain
return bestFeature
myDat,labels=createDataSet()
chooseBestFeatureToSplit(myDat)
# 输出:
'''
0
'''
决策树是一种常见的机器学习算法,用于分类和回归任务。它的模型在结构上就像一棵树,包括根节点、内部节点和叶子节点,通过一系列的问题对数据进行分割,从而达到决策的目的。决策树易于理解和实现,数据的准备工作相对简单,不需要太多的数据预处理,如归一化或标准化。
决策树的构建过程是一个递归过程。从数据集的全体样本开始,选择一个最优的分割特征,按照这个特征的不同取值将数据集分割成较小的子集。这个过程在每个生成的子集上重复进行,直到满足停止条件,如子集在当前节点的所有记录都属于同一类别,或者达到预设的最大深度等。
下面的函数majorityCnt()使用多数表决的方式确定一组数据中最常出现的类别。这通常在决策树算法中用于决定叶子节点的分类,特别是当所有特征都已被用于分割数据集,但样本仍然不是纯净的单一类别时。
myDat
# 输出:
'''
[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
'''
labels
# 输出:
'''
['no surfacing', 'flippers']
'''
# 多数表决决定叶子结点的分类
import operator # 用于排序操作
def majorityCnt(classList): # 列表参数包含了一系列分类标签
classCount={} # 初始化一个空字典classCount用于存储每个类别的出现次数
for vote in classList: # 遍历
if vote not in classCount.keys():classCount[vote]=0
classCount[vote]+=1 # 无论之前是否存在,都对当前类别的计数加一
sortedClassCount=sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
# 创建树的函数代码
def createTree(dataSet,labels):
classList=[example[-1] for example in dataSet]
print(classList)
if classList.count(classList[0])==len(classList):
return classList[0]
if len(dataSet[0])==1:
return majorityCnt(classList)
bestFeat=chooseBestFeatureToSplit(dataSet)
bestFeatLabel=labels[bestFeat]
myTree={bestFeatLabel:{}}
del(labels[bestFeat])
featValues=[example[bestFeat] for example in dataSet]
uniqueVals=set(featValues)
for value in uniqueVals:
subLabels=labels[:]
myTree[bestFeatLabel][value]=createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
return myTree
myDat,labels=createDataSet()
myTree=createTree(myDat,labels)
myTree
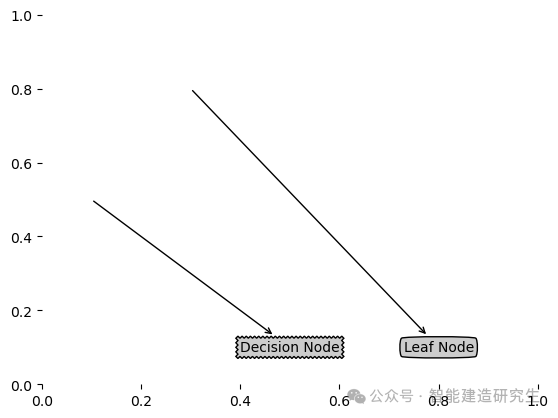
# 使用文本注解绘制树节点
import matplotlib.pyplot as plt
decisionNode=dict(boxstyle="sawtooth",fc="0.8")
leafNode=dict(boxstyle="round4",fc="0.8")
arrow_args=dict(arrowstyle="<-")
def plotNode(nodeTxt,centerPt,parentPt,nodeType):
createPlot.ax1.annotate(nodeTxt,xy=parentPt,xycoords='axes fraction',xytext=centerPt,textcoords='axes fraction',
va="center",ha="center",bbox=nodeType,arrowprops=arrow_args)
def createPlot():
fig=plt.figure(1,facecolor='white')
fig.clf()
createPlot.ax1=plt.subplot(111,frameon=False)
plotNode('Decision Node',(0.5,0.1),(0.1,0.5),decisionNode)
plotNode('Leaf Node',(0.8,0.1),(0.3,0.8),leafNode)
plt.show()
createPlot()
以上内容总结自网络,如有帮助欢迎转发,我们下次再见!