何似清歌倚桃李
一炉沈水醉红灯

契子 ✨
上一期给大家提供了大概会考的题型给老铁们复习的大致思路
这一期还会是一样,我将整理一下排序的题型以及解题方法给你们

由于时间还很多,我就慢慢总结吧,一天一章的样子,明天总结串、后天总结图
然后坦然的走向期末考的刑场
我们还是先来讲一下排序吧?我对这块比较熟
排序重点考快排的方法,分析时间复杂度、稳定性
考排序的话,快排是必考的,因为太重要了
如果快排还不懂的老铁,可以去看看我之前的文章:手撕快排(点击链接即刻跳转)
我们二叉树中不是还有个堆吗?我遇到的题中往往是结合排序来考的 -- 堆排序。题型大概就是初始化建堆。如果还有对堆了解还不够深刻的老铁,请看这篇文章:堆排序
然后其他的题型便是:给出一些排序考你稳定性以及时间复杂度了,这里稍微去翻一下课本就行
(1)快排(常考排完一次快排后的序列)大概率会考 == 必考
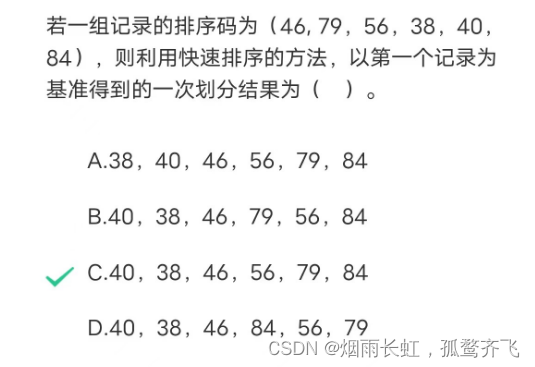
我说的都是有根据的,都是自己做到的作业题以及结合一些考试因素,所以可以选择相信我
(2)堆排序(初始化建堆)高几率
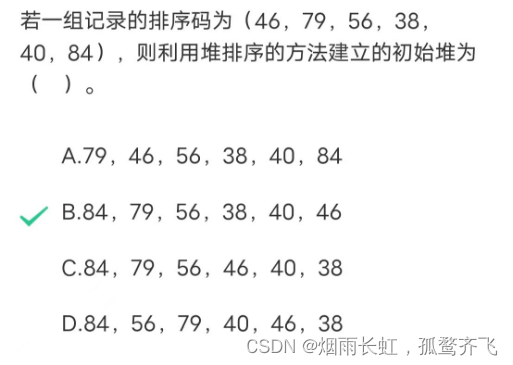
(3)时间复杂度、稳定性(感觉排序也少不了的一环)
(4)环境题 -- 给出一个案例让你选择最优排序(这个很少见,考对所有排序的概念理解,但是学校应该不会为难你吧,不放心的话可以看看)
排序的考点大概就是这些,考的不多大概就两三道打底的样子(一本正经的分析)
但是这分能捡就捡,说不定离不挂科就差这几分呢?

废话说完了,直接上题吧 ~
快排的模拟
我们把这一类题称为快排的模拟,因为方法就是画图模拟快排的实现
以30为基准,设一组初始记录关键字序列为(30,15,40,28,50,10,70) 则第一趟快速排序结果为() A、10,28,15,30,50,40,70 B、10,15,28,30,50,40,70 C、10,28,15,30,40,50,70 D、10,15,28,30,40,50,70我先教老铁们模拟一遍,在公布答案:
首先说明一下快排的常识(排序思想)吧 ~ 为了以下好讲(为了照顾小白)快排思想
任取待排序元素序列中的某元素作为 基准值 ,按照该排序将待排序集合分割成两子序列,左子序列中所有元素均 小于 基准值,右子序列中所有元素均 大于 基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
而我们之前的方法则是双指针思想:模拟两个指针 left、right 分别指向首尾位置,然后 right 先找比基准小的元素,left 再找比基准大的元素,找到后交换。重复以上步骤,直到两者相遇。在这个时候,我们的相遇点的元素与基准值进行交换这样我们的一趟快排就结束了
(觉得很空洞的可以看我之前的博客)
但是如果我们做选择题的话还有简单方法,我们就不用以上方法了,我之所以提一下以上方式只是为了让大家回顾一下快排而已,接下来我将在题目的讲解中教会大家这种方法
对于模拟题的最好解法就是画图:
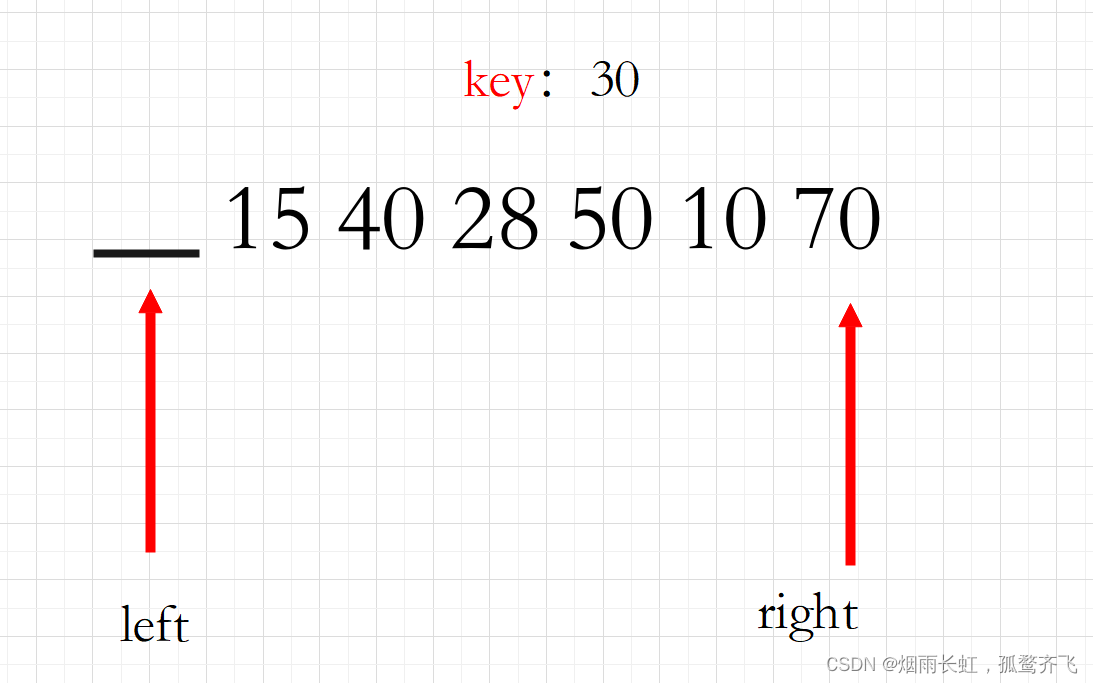
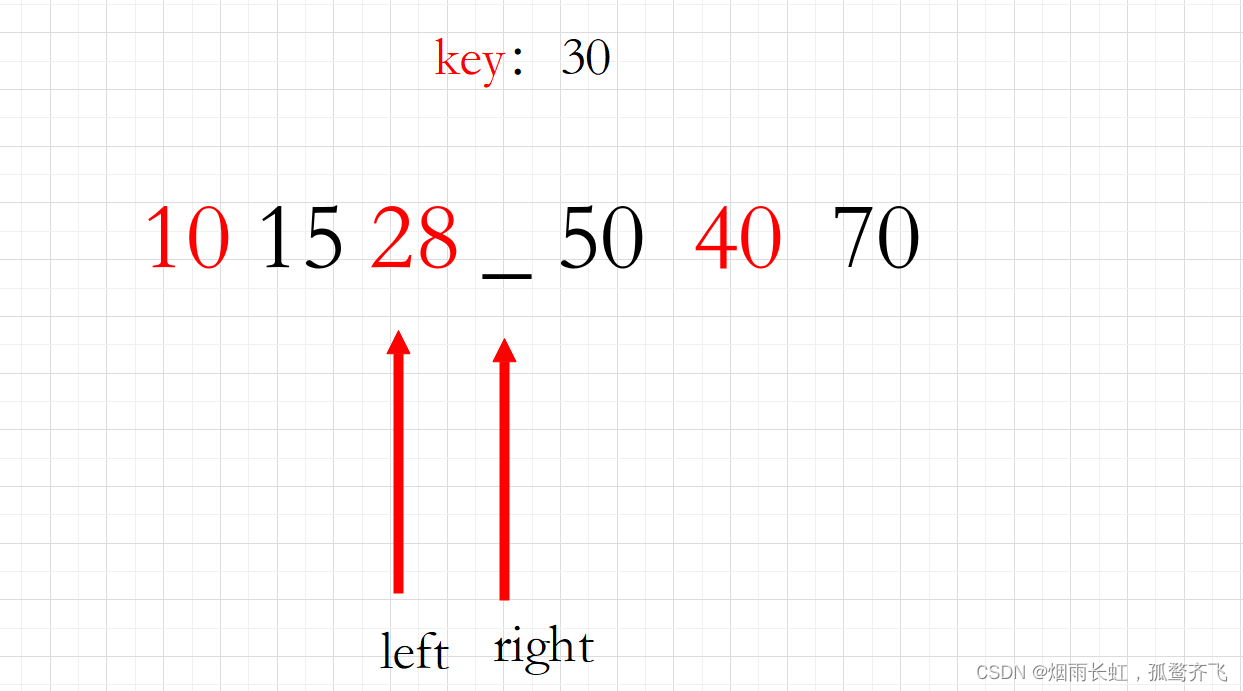
<1>根据题目的要求我们选择 30 作为基准 key,一般都是第一个位置的元素作为基准,然后我们依旧是采用双指针,也就是 left 指向剩余元素的起始位置,right 指向剩余元素的末尾位置,如下图所示:
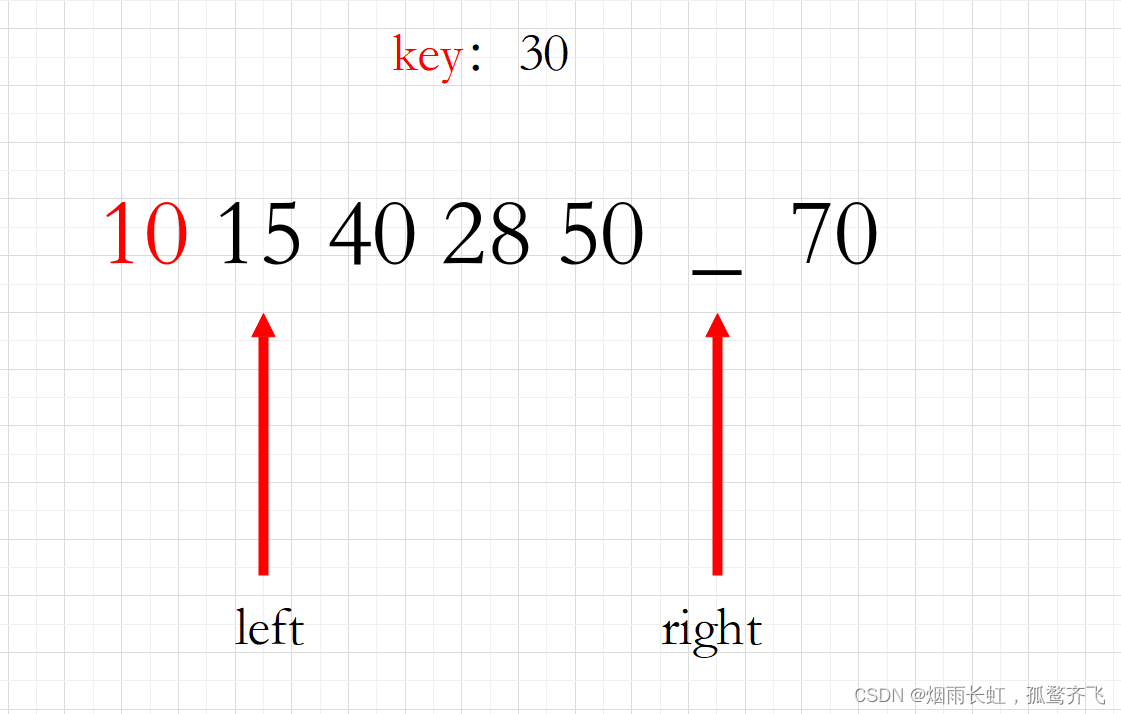
<2>我们将基准元素单独拉出来,留有一个空缺位置,像这样:
这个时候准备工作已经做完了,可以开始操作了
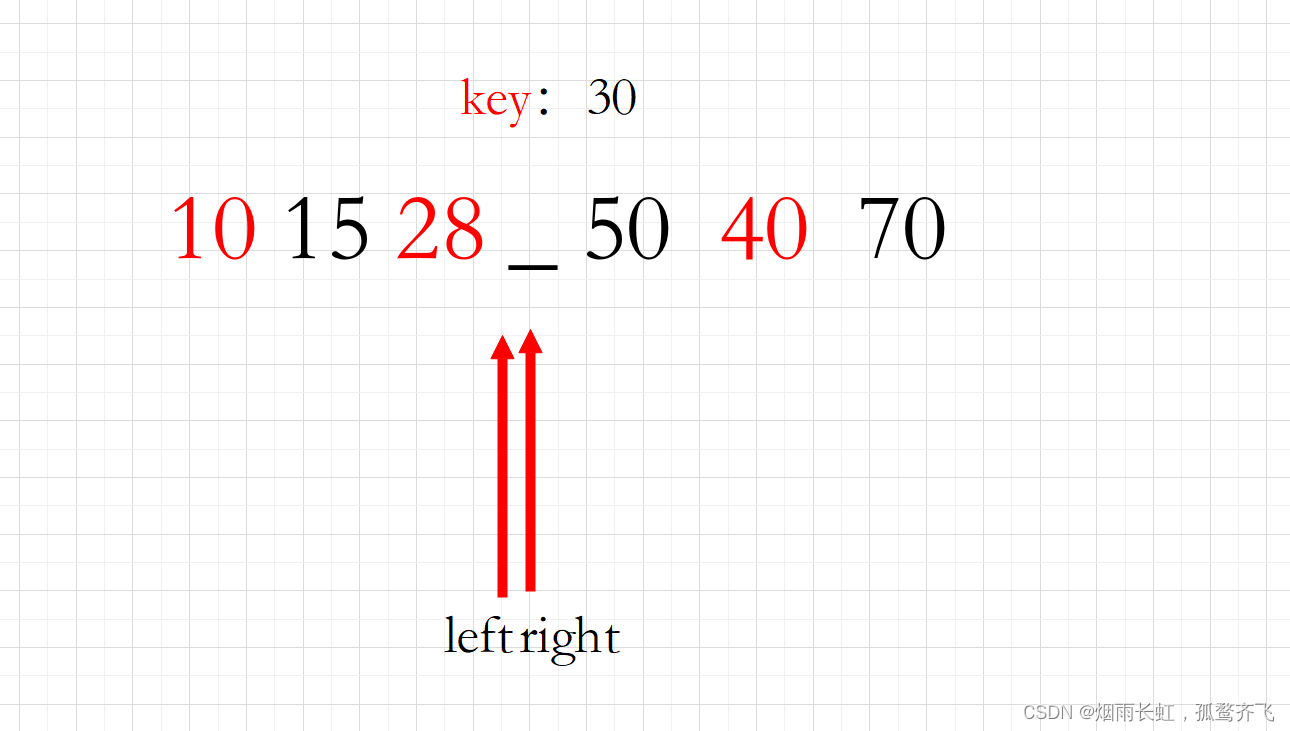
<3>我们先从右边开始找到比基准值还要小的元素
我们找到的元素是 10,就塞到那个空缺的位置中
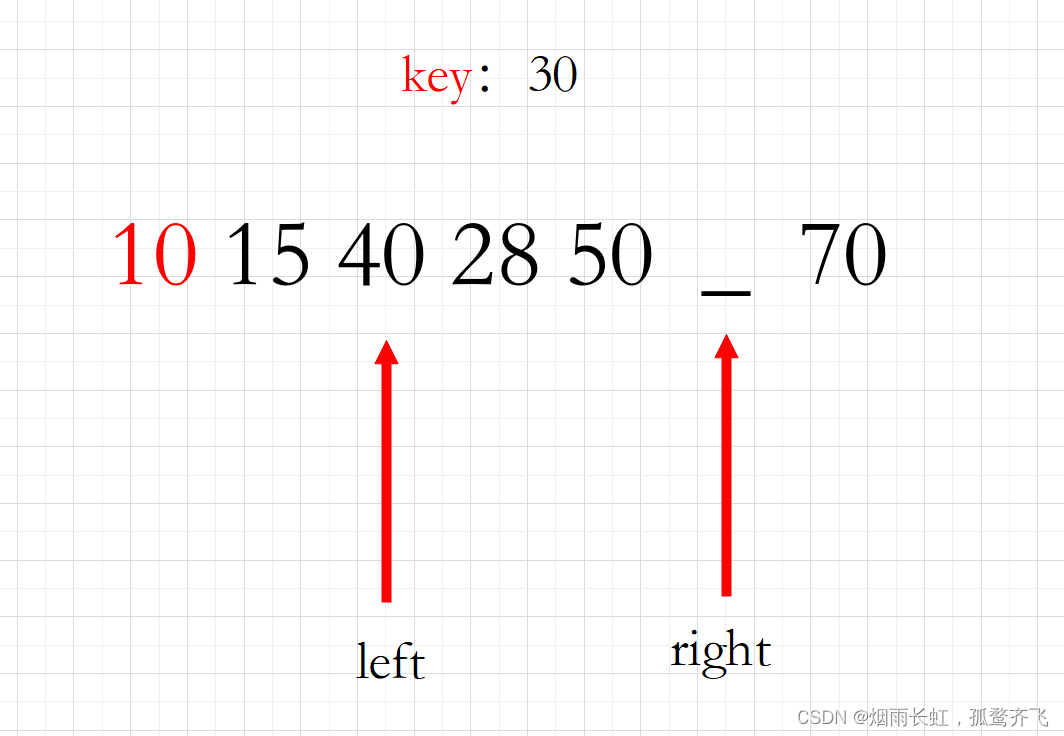
<4>其次我们从左边开始找比基准值大的元素
我们找到的是 40 也塞到空缺的位置中
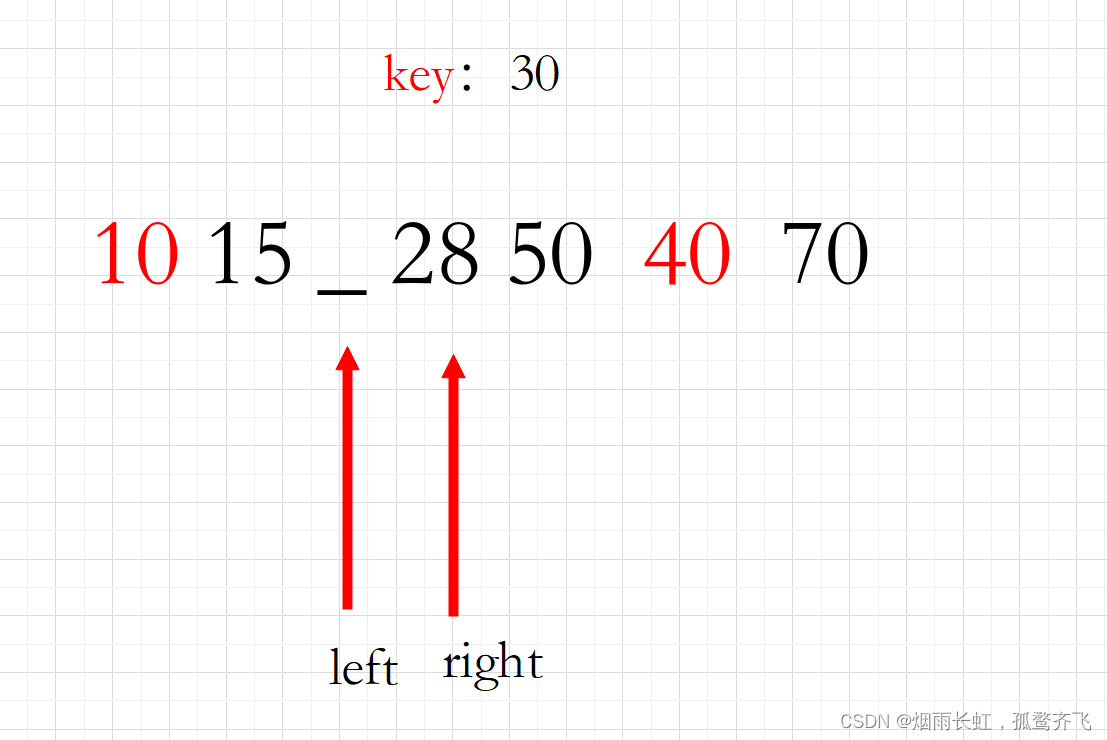
重复以上操作
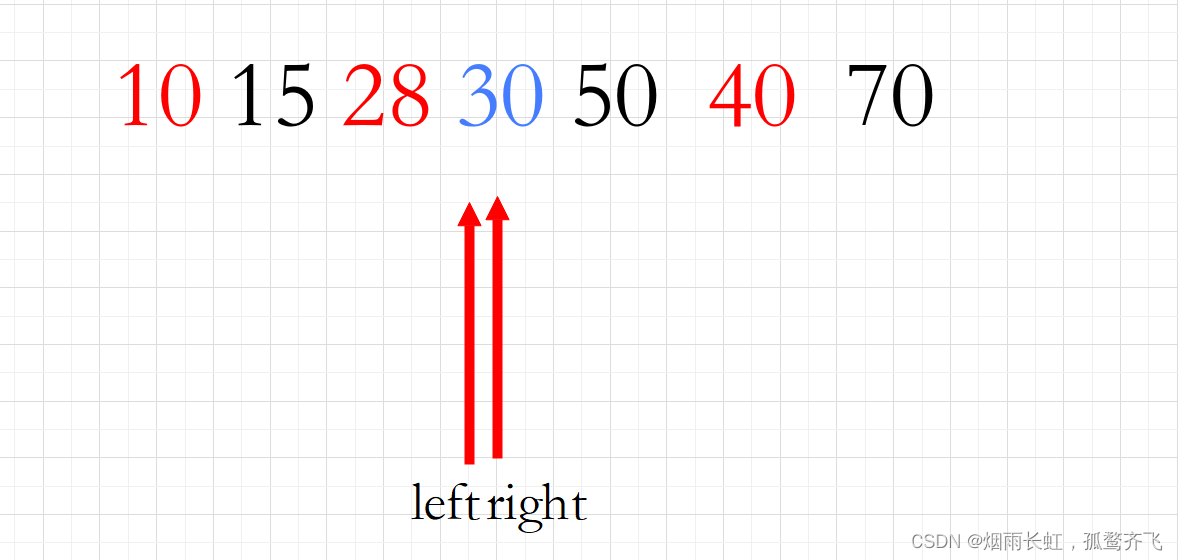
<5>当我们的双指针重叠时,就将 30 塞回空缺位置中
这样我们就完成了一趟快排,实在不知道为什么这样做的老铁先去看一下快排吧,我这里只教方法
这道题的正确答案:B
也不知道,大家对上题了解了多少,这里再提供一道
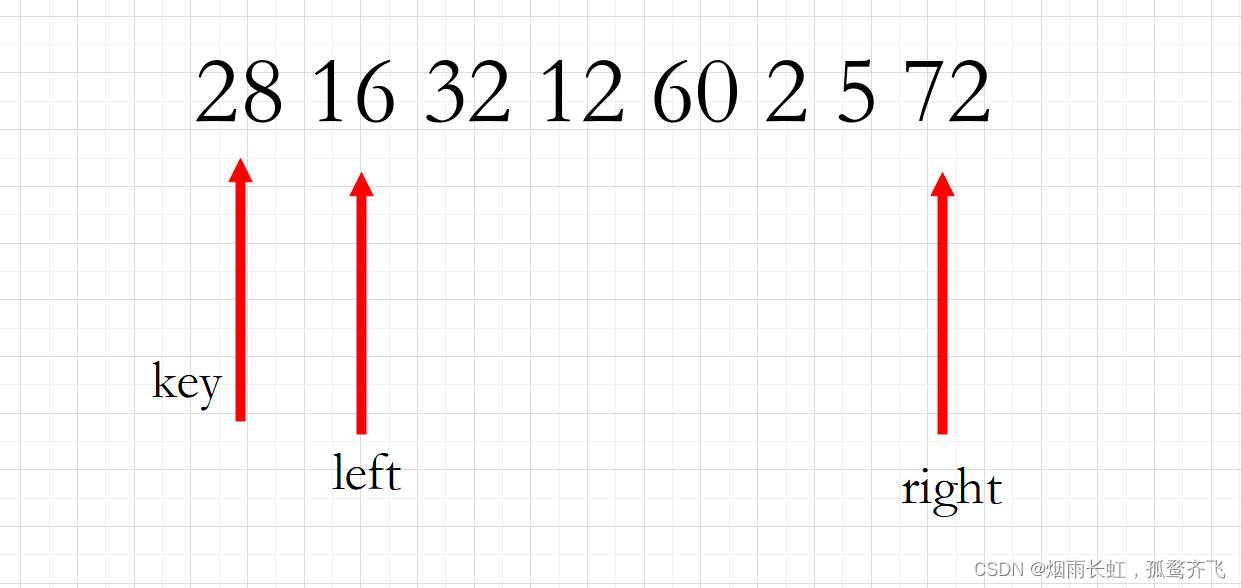
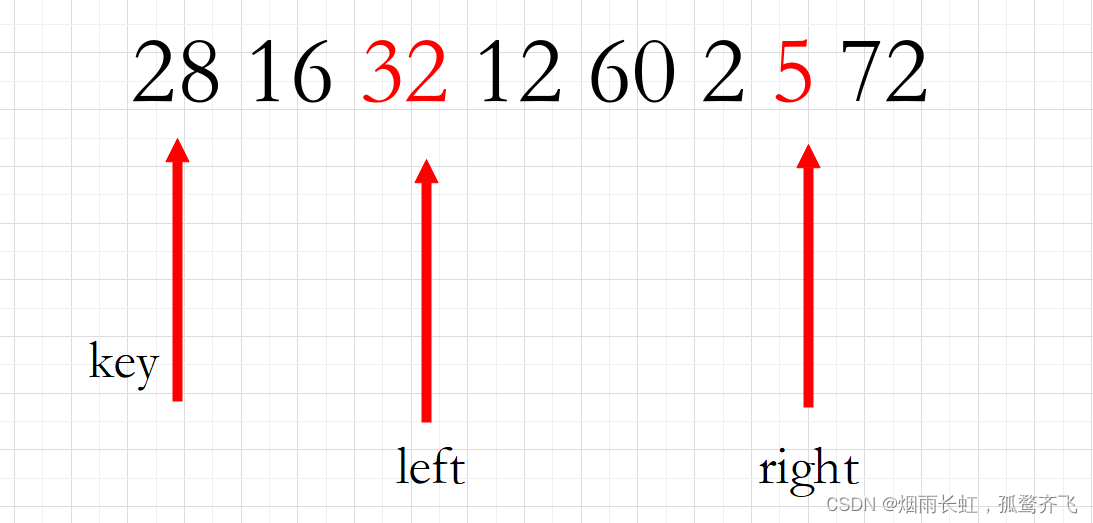
对数字序列28 16 32 12 60 2 5 72进行升序的快速排序(以第一个关键码为基准的方法) 一次划分后的结果为() A.2 5 12 16 28 60 32 72 B.2 16 5 12 28 60 32 72 C.2 16 12 5 28 60 32 72 D.5 16 2 12 28 32 60 72我们这次干脆换一种方法吧 ~ 用我们快排的原始方法:
一开始与上面那题同理,找到基准,再固定双指针
<1>右边开始先找小于基准的元素,左边再找大于基准的元素
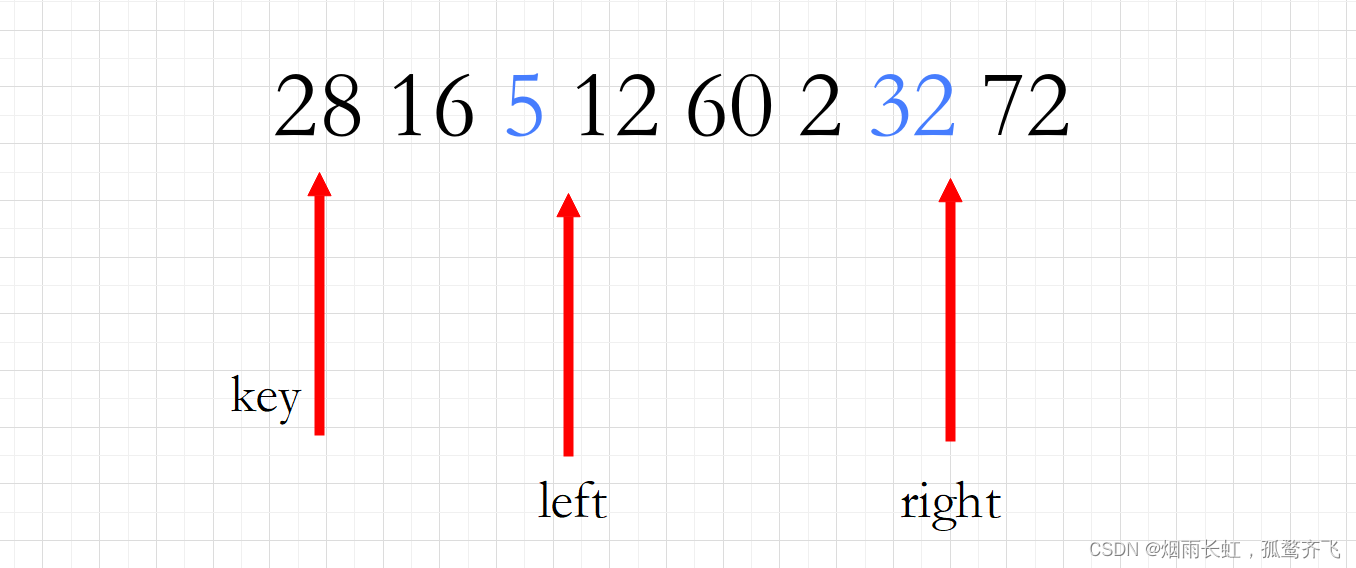
我们找到的是 5 后,左边在开始找
<2>数据都找到了便交换两者的数据
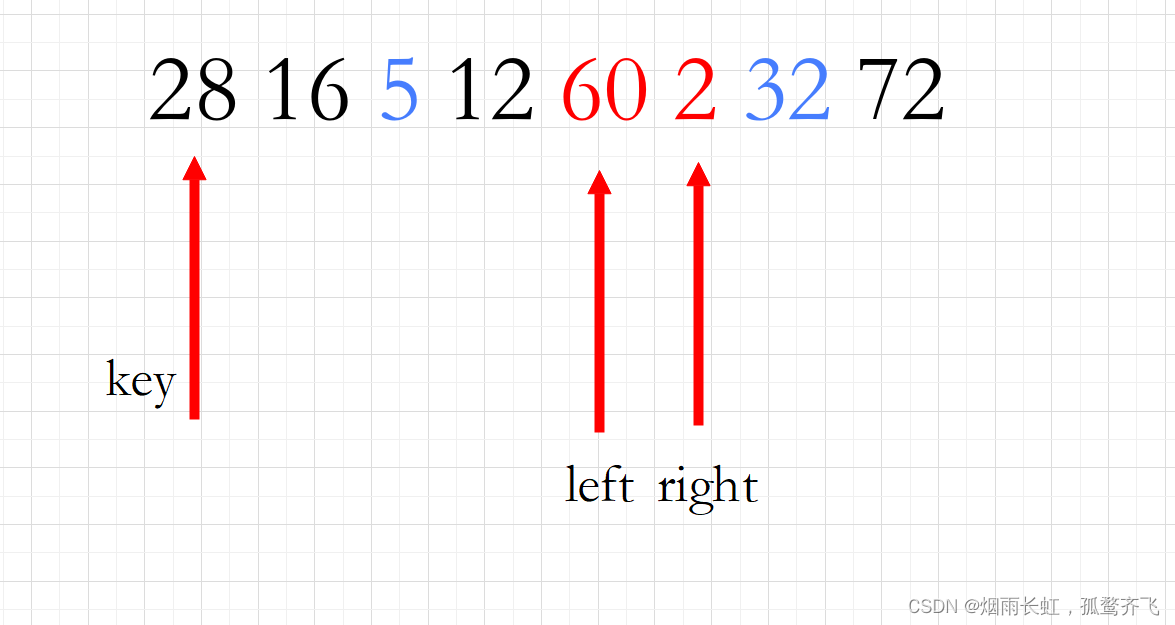
<3>重复以上步骤
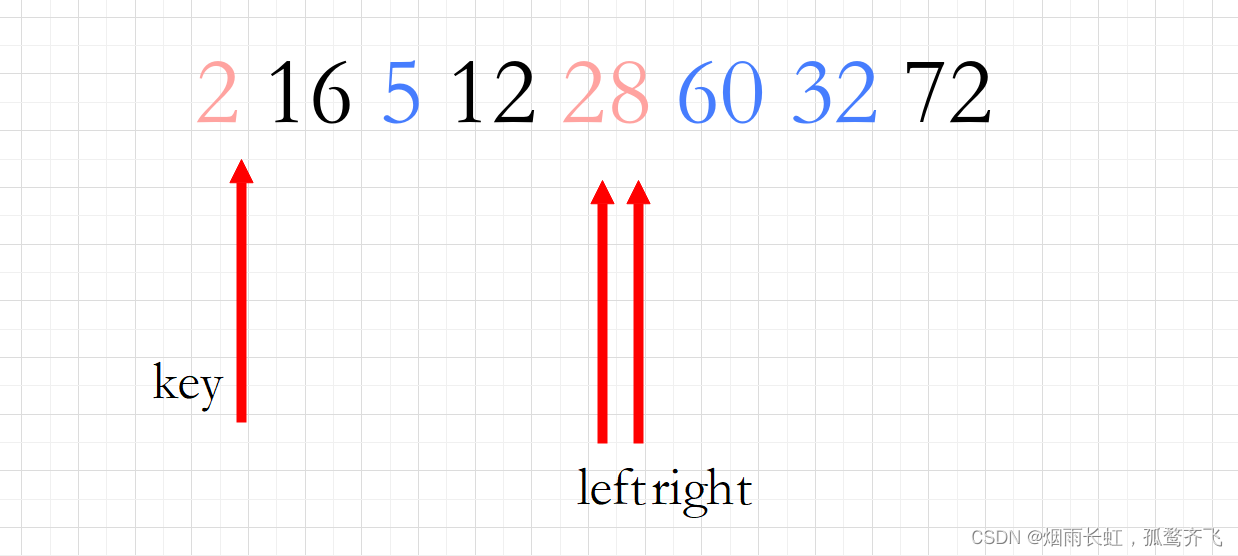
<4>当两个指针相遇时,便让当前数据与基准值 key 做交换
所以答案选择:B
解析:
快速排序以基准值为中心,对元素进行划分,这里 28 为基准值,则小于 28 的和大于 28 的进行交换,完成一次划分
这样我们的快排模拟的题型就告以段落吧,接下来我们来看看堆排序的题型
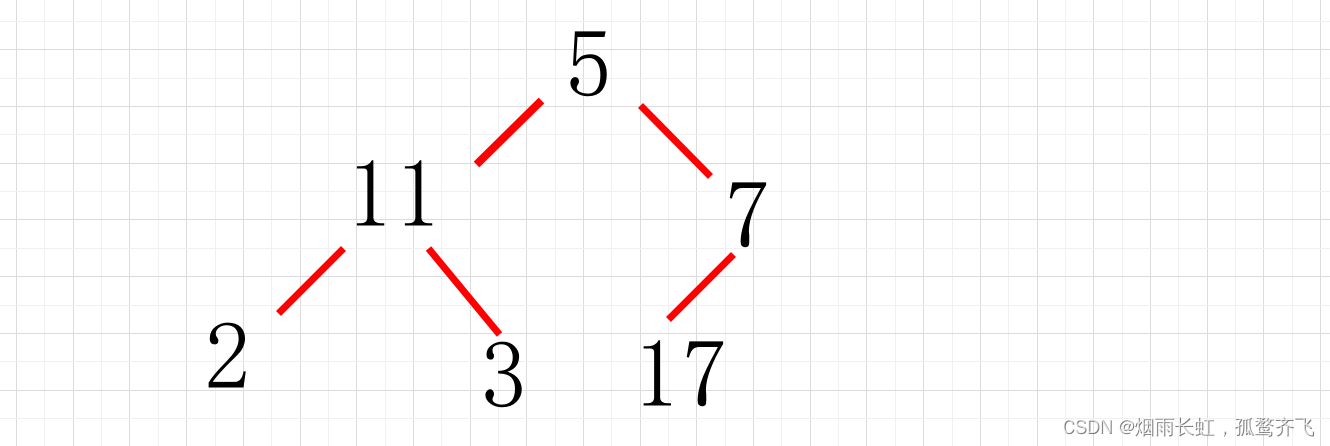
现有数字序列 5 11 7 2 3 17,目前要通过堆排序进行降序排序 那么由该序列建立的初始堆应为() A.2 3 7 11 5 17 B.17 11 7 2 3 5 C.17 11 7 5 3 2 D.2 3 5 7 11 17我们先来分析一下题目,对堆还不了解的去点上面的链接:
这里说进行降序排序,所以我们要建小堆,每次把堆顶元素放在当前堆的最后一个位置
建堆要进行向下调整算法(从最后一个非叶子节点开始进行向下调整算法,直到根元素)
我们这里就简单的模拟一下吧:
堆简单来说就是二叉树的数组表现形式,这里我们通过堆模拟一下二叉树
然后从我们的叶子节点开始,因为我们是建立小堆,那么最小的元素肯定是排在上面的
知道这个原理我们就来开始调整
因为 2 (左孩子)比 3(右孩子)小也比 11(双亲)小
所以我们就要调整 2 与 11 的位置(根据小堆原理,最小元素排在上面)
重复上面步骤开始建堆
最后我们建堆完成后便是这个样子:
然后转化为我们的数组,所以初始堆序列为: 2 3 7 11 5 17
因此答案:A
所以像这种送分题务必拿下 ~

画图题基本上已经讲完了,我们来看一下概念题 ~

下列排序算法中,占用辅助空间最多的是() A.归并排序 B.快速排序 C.希尔排序 D.堆排序答案:A
解析:
归并排序空间复杂度:n
快排: logn
希尔、堆排: 1
下列关于排序方法和其平均时间复杂度,配对错误的是() A.堆排序——O(nlog2 n) B.直接插入排序——O(n^2) C.选择排序——O(n^2) D.归并排序——O(n^2)答案:D
解析:
归并排序是二分排序,其实际复杂度为 nlogn
下列排序方法中,每一趟排序结束时都至少能够确定一个元素最终位置的方法是( ) ① 选择排序 ② 归并排序 ③ 快速排序 ④ 堆排序 A.①④ B.①②④ C.①③④ D.①②③④这种题就考的是对所有排序的模拟了,需要你了解所有排序的实现原理,属于偏难的题目,小概率会出
答案:C
解析:
(1)选择排序每次选一个最值,放在最终的位置
(2)快速排序每次基准值的位置也可以确定
(3)堆排序每次堆顶元素的位置也可以确定
所以这三种方法都可以每次至少确定一个元素的位置
(4)归并排序每次都需要对 n 个元素重新确定位置,所以不能保证每次都能确定一个元素位置,有可能每次排序所有元素的位置都为发生变化
下列排序方法中,哪一种是不稳定的() A.直接插入排序 B.归并排序 C.选择排序 D.冒泡排序答案:C
解析:
(1)直接插入一般可以从前向后进行元素的插入,相同元素的相对位置可以不发生变化
(2)归并也可以保证相对位置不变
(3)冒泡排序在元素相同的情况下也可以不进行交互,也可以保证稳定
(4)选择排序的思想是每次选出最值,放在已排序序列的末尾,如果最值有多个,而选出的为最后一个最值,会导致相对位置发生变化
下列关于归并排序的说法中正确的是() A.归并排序不需要辅助空间 B.归并排序的时间复杂度是O(logn) C.归并排序是稳定排序 D.归并排序的操作方式类似二叉树的前序遍历答案:C
解析:
(1)归并排序需要一个辅助空间暂时保存部分区间的排序元素
(2)归并排序是一种二分排序算法,每次都需要给 n 个元素排序,排序的过程需要 logn,即树的高度,所以时间复杂度为 nlogn
(3)归并排序中,相同元素的相对位置不会发生变化,所以是稳定排序

本期就介绍到这里吧,排序的话应该考的不多,但是快排必考(经验+直觉)
我们下期再见 ~