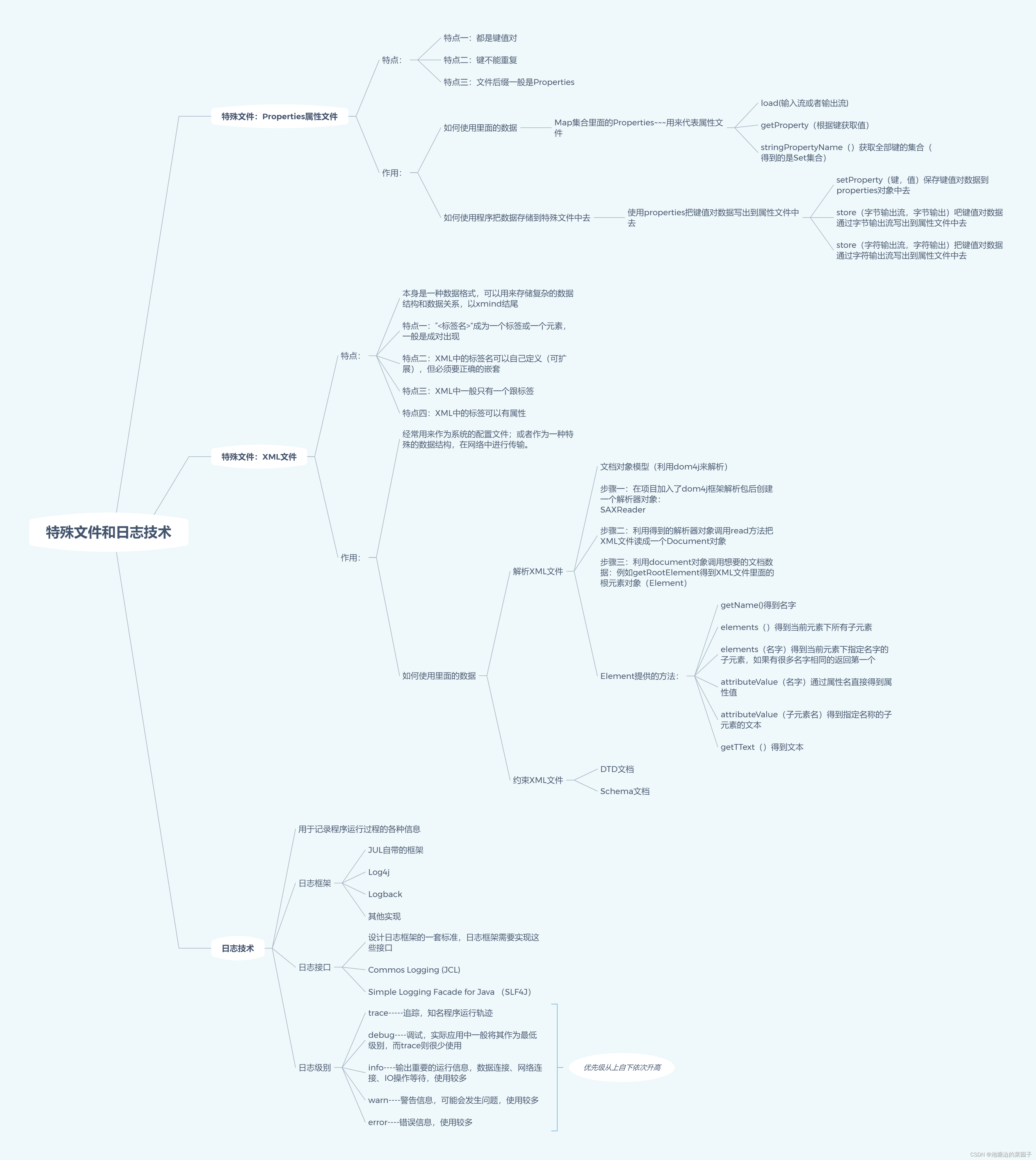
搜索引擎应该具备哪些要求
- 查询速度快
- 优秀的索引结构设计
- 高效率的压缩算法
- 快速的编码和解码速度
- 结果准确
- ElasiticSearch 中7.0 版本之后默认使用BM25 评分算法
- ElasticSearch 中 7.0 版本之前使用 TP-IDF算法
倒排索引原理
- 当我们有如下列表数据信息,并且系统数据量达到10亿,100亿级别的时候,我们系统该如何去解决查询速度的问题。
- 数据库选择—mysql, sybase,oracle,mongodb,唯一加速查询的方法是添加索引
索引
- 无论哪一种存储引擎的索引都是如下几个特点
- 帮助快速检索
- 以数据结构为载体
- 以文件的形式落地
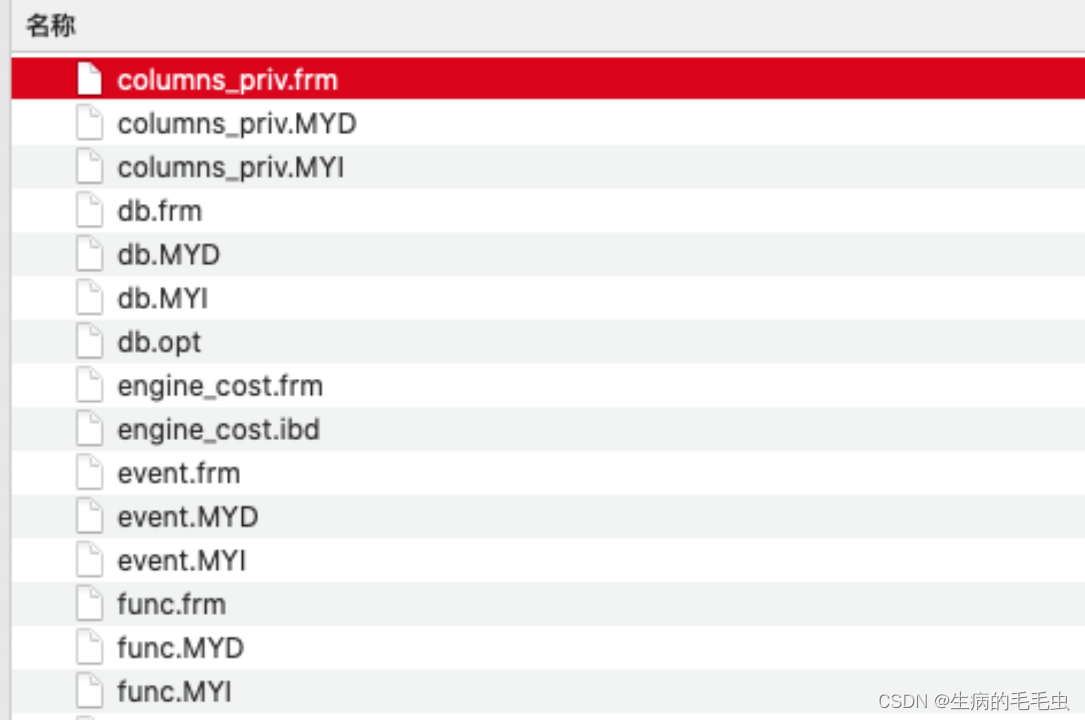
- 如下图中mysql的文件形式,其中的idb文件就是使用innodb存储引擎来实现数据存储生成的文件,其他后缀的文件是其他存储引擎生成的,因此无论什么引擎,索引方式,数据结构最终都是要落文件的
- 传统数据库的基本结构如下:

- MySql包括Server层和存储引擎层:Server层包括,连接器,查询缓存,分析器,优化器,执行器
- 连接器:负责和客户端建立连接
- 查询缓存:MySql获取到查询请求后,会先查询缓存,如果之前已经执行过一样的语句结果会以Key-value的形式存储到内存中,key是查询语句,value是查询结果。缓存明中的话可以很快完成查询,但是大多是情况不能明中,不建议用缓存,因为缓存失效非常频繁,任何对表的更新都会让缓存晴空,所以对一个进程更改的表而言,查询缓存基本不可用,除非是一张配置表。可以通过配置来决定释放开启查询缓存,并且MySql8.0 之间删除了查询缓存功能
- 分析器:词法分析,识别语句中表名,列名,语法分析,判断Sql是否满足MySql语法
- 优化器:在有多个索引的情况下,决定使用哪个索引,或者多表联合查询的时候,表的连接顺序这么执行等
- 执行器:执行器先判断权限,有权限才会去调用存储引擎对应的查询接口,默认InnoDB
数据载体 mongodb & mysql
- 以为mongodb为案例,索引数据存储的结构如下
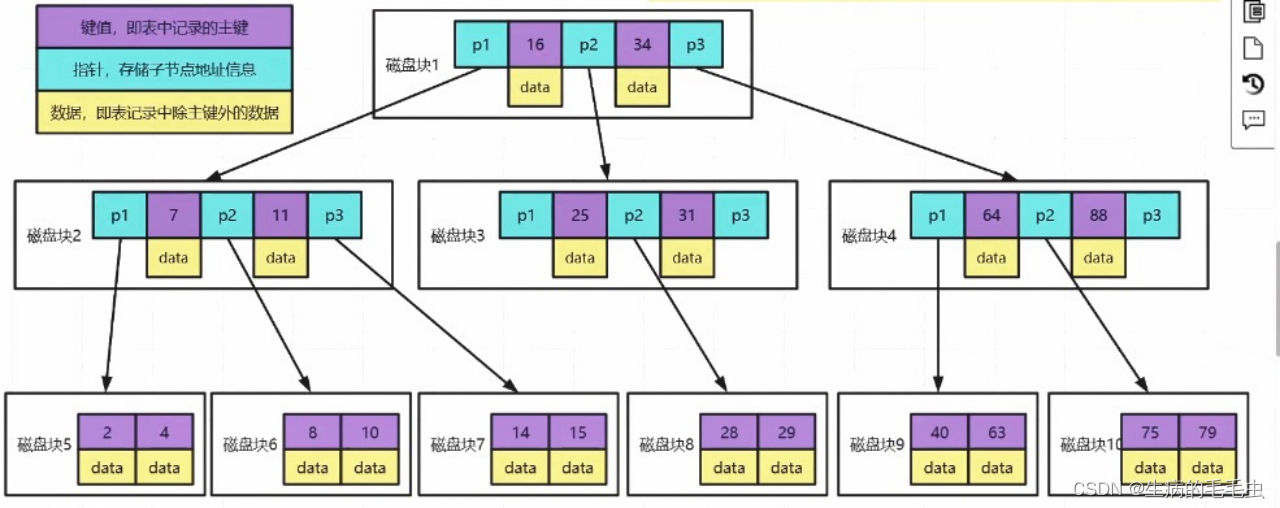
-
Mongodb索引使用的是B树:B树是多叉平衡查找树,包括以下几个结构特性
- 左子树数据小于跟数据,右子树数据大于根节点数据
- 左右子树高度差不大于1
- 每个节点可以有N个字节的,N>2
-
B树的每个节点都存放 索引 & 数据,数据遍布整个树结构,搜索可能在非叶子结点结束,最好情况是O(1)
-
B树存在的问题:
- 紫色部分存储数据的主键信息,蓝色存储的是指针指向下一个节点,黄色部分是存储的主键对应的数据Data。因此Data是在节点中占比最大的一部分数据,他可能有1M或者更大的一个数据体
- 假设我们一个节点的大小是固定的M,在Mysql中最小的数据逻辑单元是数据页,一个数据页是16KB,如果Data越大,M所能容纳的Data个数就越小,如果需要存储更多的数据则需要更多的节点,B树为了承载更多的节点的同时满足结构特性就需要更多的分叉,因此就导致树的深度更大,每一个层级都意味着一次IO操作导致IO次数更多
-
以为Mysql为案例分析:
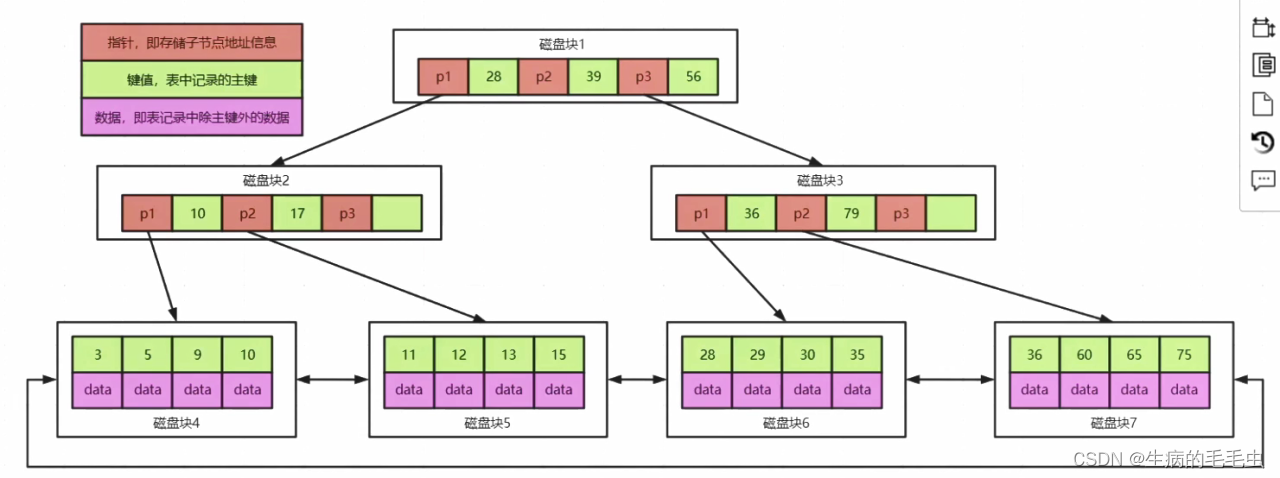
- Mysql中innoDB 使用的索引结构是B+树,
- B+ 树是B树的变种,区别在于:
- 叶子结点保存了完整的索引 & 数据,非叶子结点只保存索引值,因此他的查询时间固定为logn
- 叶子结点中有指向下一个叶子结点的指针,叶子结点类似一个双向链表
- 因为叶子结点有完整数据,并且有双链表结构,因此我们在范围查询的时候能有效提升查询效率。
- 数据都在子节点上,因此非叶子节点就能容纳更多的索引信息,这样就增加了同一个节点的出度,减少了数据Data信息,同一个节点就能容纳更多的其他类型数据信息,因此能用更少的节点来承载索引数据,节点的减少导致树的深度更低,查询的IO次数就变少了。
倒排索引数据结构
- 对如上两个索引结构的分析,我们能看到MySql 无法解决大数据索引问题:
- 第一点:索引往往字段很长,如果使用B+trees,树可能很深,IO很可怕
- 第二点:索引可能会失效
- 第三点:查询准确度差,
- 有如下案例,有1亿条数据的商品信息,我们需要对其中的product字段进行查询,而且是文本信息查询,例如“小米”这个字段查询,那么有如下查询语句:
select * from product where brand like "%小米 NFC 手机%"
-
第一点说明:以上查询语句,我们需要在product上建索引, MySql上使用的B+树,因为文本的信息量特别的大,导致所需要的节点就更多N个16KB(MySql索引中如果一个数据行的大小超过了页的大小16KB,MySQL 会将该行的部分数据存储在行溢出页中。这意味着数据行会被分割,一部分存储在索引页中,而溢出的部分存储在单独的溢出页中),节点数的增加,导致树深度增大查询IO次数增加

-
第二点说明:“%小米 NFC 手机%” 查询中用了左匹配的方式去查询,会导致索引失效,这样导致全表扫描。
-
第三点说明:“小米 NFC 手机%” 去掉左匹配,走索引的方式,则会只查询"小米 NFC 手机"开头的,这样就会导致结果不准确
ElascitSearch索引解决方案
- 对product字段进行分词拆分,得到如下一个词项 与id的匹配关系如下

Posting List (倒排表)
- 索引系统通过扫描文章中的每一个词,对其创建索引,指明在文章中出现的次数和位置,当用户查询时,索引系统过就会根据事先建立的索引进行查找,并将查找的结果反馈给用户的检索方式,利用如上表可以快速完成全文检索
- 在为属性(product)构建倒排索引后,此时,本类别中包含了所有文档中所有字段的一个 分词(term) 文档id对应关系的字典信息,通过倒排索引我们可以迅速找到符合条件的文档,例如“手机” 在文档 1,2,3 中。
Term Dictionary(前缀树)
- 当我们进行Elasticsearch查询,为了能快速找到某个term在倒排表中的位置,ElasticSearch 将类型中所有的term进行排序,然后通过二分法查找term,时间复杂度能达到 logN的查找效率,就像通过字典查找一样,这就是Term Dictionary,整个是二级辅助索引
Term Index(前缀索引)
- 同时参照 B-Tree通过减少磁盘寻道次数来提高查询性能,Elasticsearch也是采用同样的思路,直接通过内存查找term,将term Dictionary这个构建的Mapping存放在内存中。但是如果term太多,term dictionary也会很大,放内存不现实,于是有了Term Index,因此整个ElasticSearch的数据结构如下图
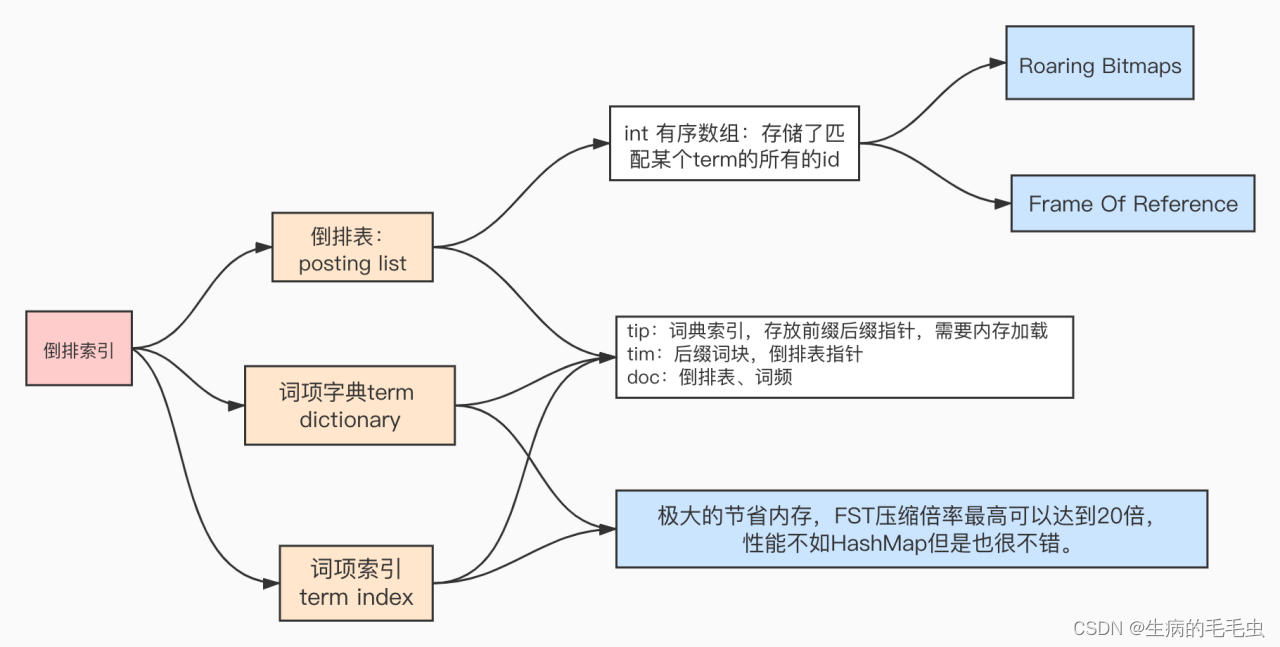
压缩算法
- 倒排表生成后,可能存在如表中,小米关键字匹配到的文档id有 100W个 int类型的有序数组,如果直接存储这个数据的那么需要4Byte * 100w =4MB 的存储空间,因此存储的时候需要用到一定的压缩算法来进行数据压缩
FOR (Frame Of Reference)压缩算法:
- 假设我们获取到的压缩表数组id是[1,2,3,4,5,…100W] 每一个数据占用的存储空间是 4Byte, 总共是100W * 4Byte = 100W * 4 * 8 bit
- 通过计算相邻数据差值 得到数组2 [1,1,1,1,1,1, ,1],总共有100W个1, 这样我们可以将每一个数据用一个bit 来存储,这样就只需要 100W * 1bit 相比于原来 数据 缩小了 32 倍
- 如下图:

-
当然以上是一个特殊的案例,我们用一个相对正常一点的数组来重新计算
-
原数组:[73,300,302,332,343,372] 总共 6*4Byte = 24Byte
-
差值数组:[73,227,2,30,11,29]。我们得到如下结论。 64 < 73 < 128, 128 < 227 < 256, 1<2<4, 16 < 30<32, 8<11<16, 16 < 29 <32,
-
以上数据我们就依然用bit位的存储方式,我们用以上数组中最大的数字所需要的bit位来计算,也就是227 ,用256 来存储 2 8 , 也就是8个bit位每个数字,得到如下
-
[73,227,2,30,11,29]。需要的存储。6 * 8bit = 48bit
-
但是我们发现还是可以有优化空间,比如 2 其实只需要一个bit位即可,因此我们将大数,小数再次做一次分组 [73, 227] 最大28 es中会做一个记录,记录此处数组占用的是8bit。, [2, 30,11,29] 最大25 同样es中做记录此处占用5bit,进一步缩小存储空间。
-
计算整个的存储空间:
- [73, 227] 部分。 8bit - 给es记录存储空间大小是8bit。数字占用 8bit * 2 总共。 8bit * 3 = 3Byte
- [2, 30,11,29] 部分。 8bit - 给es记录存储空间大小是5bit, 数字占用 5bit * 4 总共。8 bit + 20bit = 4Byte
- 因此总共也就7 Byte的空间占用
-
如下图:

RBM压缩(Roaring bitmaps)
-
有了FOR算法,而且针对于同一种数据结构为什么还需要RBM算法,因为以上数据中案例数组都是比较稠密的数组,也就是他们的差值都是比较小的值,如果有如下数组
-
[1000W, 2000W, 3000W, 4000W, 5000W] 每个数都上千万,差值也是千万级别,这样用FOR算法就没有任何意义了。
-
RBM 案例讲解,有如下案例[1000, 62101, 131385, 132052, 191173, 196658]
-
第一步,我们将数字用二进制表示 ,例如。196658 转二进制是 0000 0000 0000 0011 0000 0000 0011 0010
-
第二步,将二进制分为高16 位: 0000 0000 0000 0011 转十进制是 2,底16位 0000 0000 0011 0010 转十进制是50
-
通过以上步骤我们得到196658 的表示方式(2, 50)
-
也可以通过计算方式得到这两个数字 196658 / 216 得到的值是2, 余数是 50 ,这种计算方式得到我们的推测结果,并且得到的所有数字都小于 2 16= 65536
-
我们将以上数组表示为 [(0,1000), (0,62101), (2,313), (2,980), (2,60101), (2,50)]
-
第三步:用一个container的数据结构来存储以上得到的数据表,
| short[] 数组存储 第一个数字 | Array,bitmap,run 存储第二个数字的组合 |
|---|---|
| 0 | 1000. 62101 |
| 2 | 313,980, 60101,50 |
| 。。。。 | 。。。。 |
- 我们将数字以第一个数字为基准做group by 聚合,得到一个表
- RBM的存储方式有三种 ArrayContainer,BitMapContainer,RunContainer 三种
- ArrayContainer存储short 类型的数组,short类型,最大是216 正好可以存储下所有数据的极限,而第一个位置中的数字,最大也就是65535,因为我们通过X/65535 X最大也就是232 因此,最多也就是。65535个行,同样一个Array最多也是存储65536个id,计算总存储占用
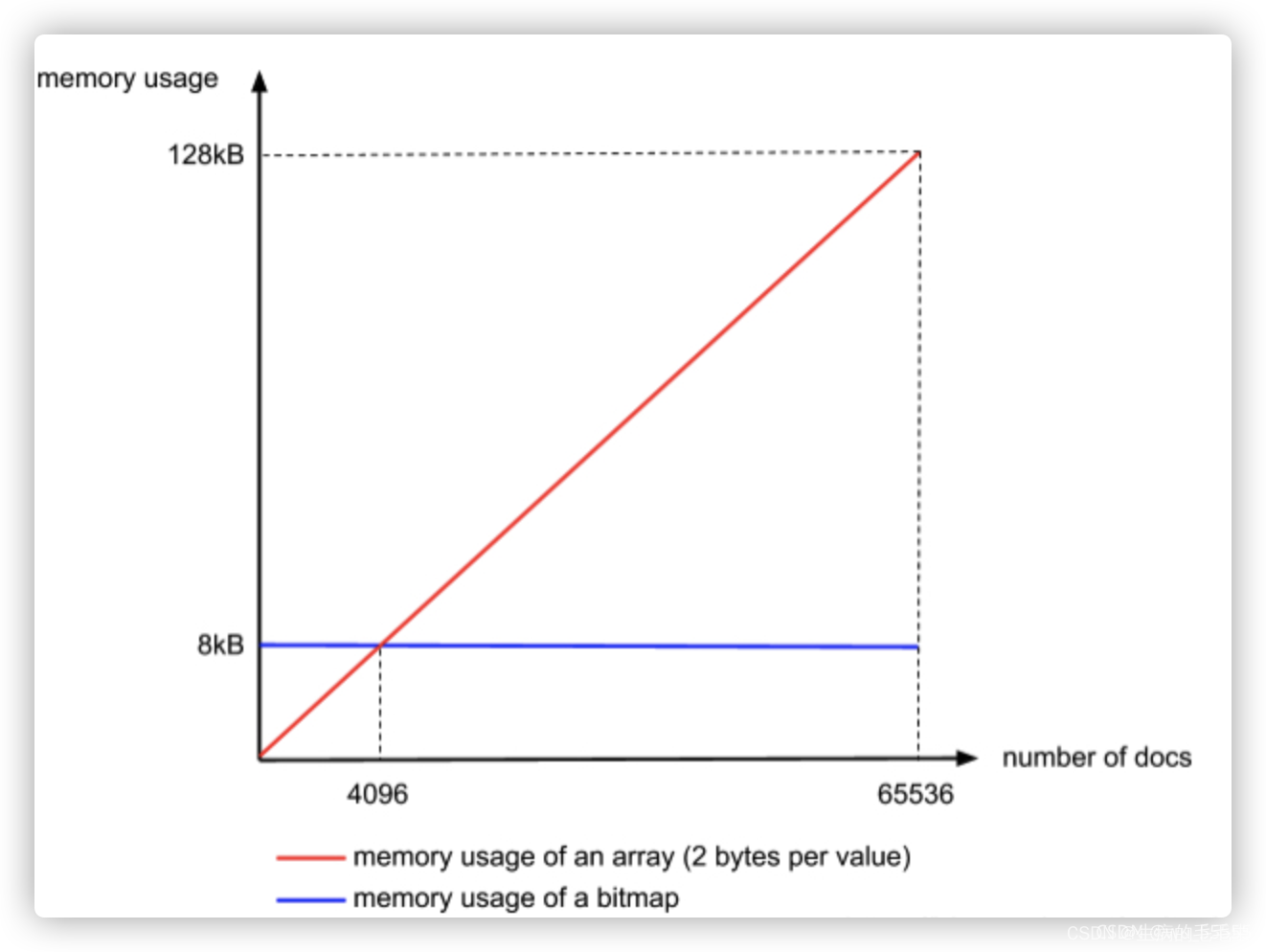
- short 2Byte = 16bit, 总共有65536个。65536* 2Byte / 1024 = 128KB,因此一个行的数据最多存储128KB
- BitMapContainer存储位图,存储的数据必须是不一样的数据,因为避免冲突,bitmap每一位不为0 的位都代表当前位的数据存在,比如第10位 1,表示数组中存在1 ,因此如果有数组[1,2,3,4,5,6,7], bitMap对应的就是7个bit位
- 如果65536 个数字都是不一样的,那么用一个 65536 个bit位置的bitMap存储即可,总共 65536 bit / 8 / 1024 = 8KB
- 缺点是必须每个数字不一样
- RunContainer存储:按照如上思路如果存在如下特殊的数组[1,2,3,4,5,…100W] ,那么可以表示为(1, 100W)压缩到极致,比例取决于连续数字的多少
- 安以上三种算法,有如下图表示

Term Dictionary & Term Index
- 构建好倒排表之后,就又能力快速找到某个term对于的文档id,然后通过id查找磁盘上的segment,新的问题产生了,加入又1亿数据,那么term可能又上百万,挨个便利就炸了
- ElasticSearch为了快速找到对应term,讲term按数组排序,排序后二分查找,以logN的查询时间复杂度完成查询,这样就构建了一个类似如下的term Dictionary
[aaa, aba, abb,abc, allen, .... ,sara,sarb,sarc,....selena.....]
- 即使是logN的时间复杂的,在存在磁盘操作的情况 + 大数据量情况也是非常慢的,如果讲term dictionary加载到内存,十万级别的数据量可能就把内存沾满了,因此需要另外一个更晓的数据来对term dictionary进行替代到内存中进行查询,他就是 term index
- 构建term index 过程: 便利所有 term dictionary 中的数据,按字符拆分,构建成b-tree,例如aaa 构建成 a-a-a,其他分支依然按字符拆分,如下图
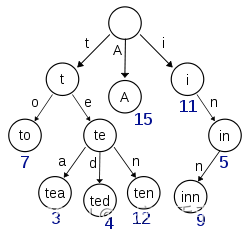
- 以上前缀表中不会包含所有的term信息,它包含的是term的前缀信息,例如 aaa,aab,aac 都存在aa前缀,通过term index可以快速地定位到term dictionary的某个offset,再结合FST(Finite State Transducers)的压缩技术,可以使term index缓存到内存中。从term index查到对应的term dictionary的block位置之后,再去磁盘上找term,大大减少了磁盘随机读的次数。如下图:
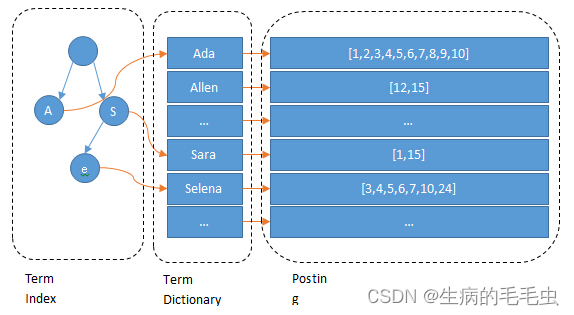
FST 压缩算法
- 假设我们要将mop, moth, pop, star, stop and top(term index里的term前缀)映射到序号:0,1,2,3,4,5(term dictionary的block位置)。最简单的做法就是定义个Map<string, integer=“”>,大家找到自己的位置对应入座就好了,但从内存占用少的角度看可以用FST来进行压缩后在存储到内存。如下图
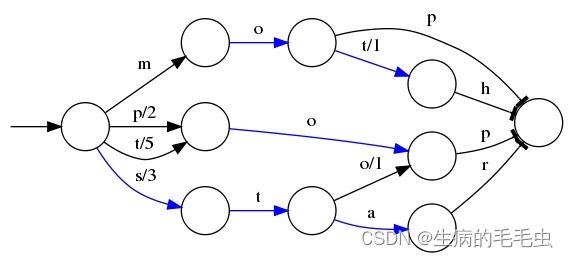
- O表示一种状态
- –>表示状态的变化过程,上面的字母/数字表示状态变化和权重
- 将单词分成单个字母通过⭕️和–>表示出来,0权重不显示。如果⭕️后面出现分支,就标记权重,最后整条路径上的权重加起来就是这个单词对应的序号。
- FST以字节的方式存储所有的term,这种压缩方式可以有效的缩减存储空间,使得term index足以放进内存,但这种方式也会导致查找时需要更多的CPU资源。


![[深度学习] 变分自编码器VAE](https://img-blog.csdnimg.cn/direct/09316755250e4df198b039245ecda94e.png)