在语音信号处理和语音识别领域，梅尔频率倒谱系数（MFCC）是最常用的特征之一。本文将逐步介绍如何从音频中提取MFCC特征，并在每个步骤中进行可视化展示。

步骤 1：加载音频文件并查看波形

首先，我们需要加载音频文件并查看其波形。为了便于处理，我们将MP3文件转换为WAV格式。

from pydub import AudioSegment
import scipy.io.wavfile as wav
import matplotlib.pyplot as plt

# 转换 MP3 文件为 WAV 格式
audio_path = '/mnt/data/00000000.mp3'
audio = AudioSegment.from_mp3(audio_path)
wav_path = '/mnt/data/converted.wav'
audio.export(wav_path, format='wav')

# 读取 WAV 文件
rate, data = wav.read(wav_path)

# 绘制波形
plt.figure(figsize=(14, 5))
plt.title("Waveform of the Audio")
plt.plot(data)
plt.xlabel("Time (samples)")
plt.ylabel("Amplitude")
plt.show()

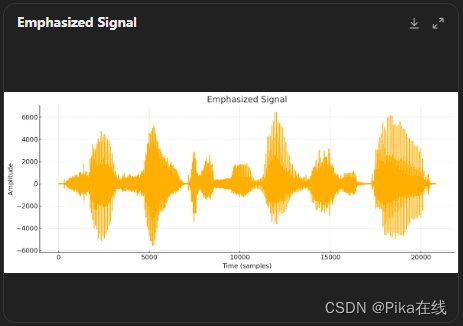
步骤 2：预加重

预加重是增强高频部分的一种方法。预加重信号可以通过以下公式实现：
$$\text{emphasized\_signal}[n]=\text{signal}[n]-0.97\times \text{signal}[n-1]$$

pre_emphasis = 0.97
emphasized_signal = np.append(data[0], data[1:] - pre_emphasis * data[:-1])

# 绘制预加重后的波形
plt.figure(figsize=(14, 5))
plt.title("Emphasized Signal")
plt.plot(emphasized_signal)
plt.xlabel("Time (samples)")
plt.ylabel("Amplitude")
plt.show()

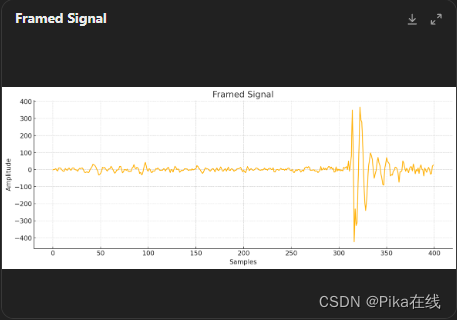
步骤 3：分帧

将信号分成重叠的帧，每帧长度为25ms，帧移为10ms。分帧可以通过以下代码实现：

frame_size = 0.025
frame_stride = 0.01
frame_length, frame_step = int(round(frame_size * rate)), int(round(frame_stride * rate))
signal_length = len(emphasized_signal)
num_frames = int(np.ceil(float(np.abs(signal_length - frame_length)) / frame_step))

pad_signal_length = num_frames * frame_step + frame_length
z = np.zeros((pad_signal_length - signal_length))
pad_signal = np.append(emphasized_signal, z)

indices = np.tile(np.arange(0, frame_length), (num_frames, 1)) + np.tile(np.arange(0, num_frames * frame_step, frame_step), (frame_length, 1)).T
frames = pad_signal[indices.astype(np.int32, copy=False)]

# 绘制分帧后的结果
plt.figure(figsize=(14, 5))
plt.title("Framed Signal")
plt.plot(frames[0])
plt.xlabel("Samples")
plt.ylabel("Amplitude")
plt.show()

步骤 4：加窗

每帧加上一个汉明窗，以减少频谱泄漏。加窗可以通过以下代码实现：

frames *= np.hamming(frame_length)

# 绘制加窗后的结果
plt.figure(figsize=(14, 5))
plt.title("Windowed Frame")
plt.plot(frames[0])
plt.xlabel("Samples")
plt.ylabel("Amplitude")
plt.show()

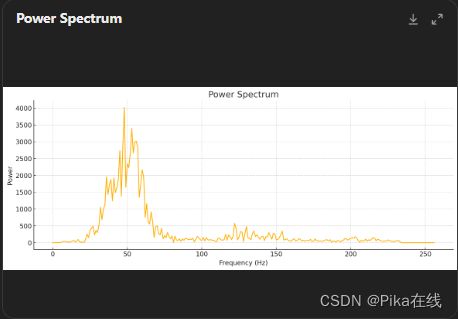
步骤 5：计算功率谱

对每帧进行傅里叶变换，计算功率谱。功率谱可以通过以下公式计算：
$$\text{Power Spectrum}=\frac{1}{NFFT}\times |\text{FFT}{|}^2$$

NFFT = 512
mag_frames = np.absolute(np.fft.rfft(frames, NFFT))
pow_frames = ((1.0 / NFFT) * (mag_frames ** 2))

# 绘制功率谱
plt.figure(figsize=(14, 5))
plt.title("Power Spectrum")
plt.plot(pow_frames[0])
plt.xlabel("Frequency (Hz)")
plt.ylabel("Power")
plt.show()

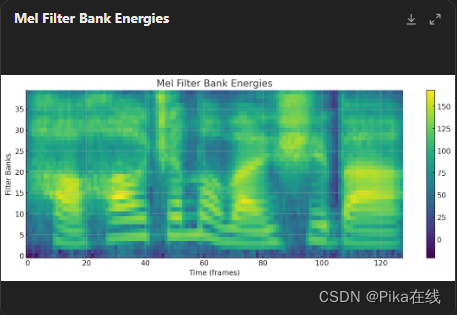
步骤 6：应用梅尔滤波器组

将功率谱通过梅尔滤波器组，得到梅尔频率能量谱。梅尔滤波器组的实现代码如下：

nfilt = 40
low_freq_mel = 0
high_freq_mel = (2595 * np.log10(1 + (rate / 2) / 700))
mel_points = np.linspace(low_freq_mel, high_freq_mel, nfilt + 2)
hz_points = (700 * (10**(mel_points / 2595) - 1))
bin = np.floor((NFFT + 1) * hz_points / rate)

fbank = np.zeros((nfilt, int(np.floor(NFFT / 2 + 1))))
for m in range(1, nfilt + 1):
    f_m_minus = int(bin[m - 1])
    f_m = int(bin[m])
    f_m_plus = int(bin[m + 1])
    for k in range(f_m_minus, f_m):
        fbank[m - 1, k] = (k - bin[m - 1]) / (bin[m] - bin[m - 1])
    for k in range(f_m, f_m_plus):
        fbank[m - 1, k] = (bin[m + 1] - k) / (bin[m + 1] - bin[m])

filter_banks = np.dot(pow_frames, fbank.T)
filter_banks = np.where(filter_banks == 0, np.finfo(float).eps, filter_banks)
filter_banks = 20 * np.log10(filter_banks)

# 绘制梅尔频率能量谱
plt.figure(figsize=(14, 5))
plt.title("Mel Filter Bank Energies")
plt.imshow(filter_banks.T, aspect='auto', origin='lower')
plt.xlabel("Time (frames)")
plt.ylabel("Filter Banks")
plt.colorbar()
plt.show()

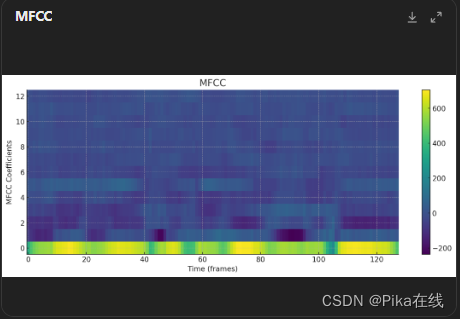
步骤 7：计算MFCC

对梅尔频率能量谱进行离散余弦变换（DCT），得到MFCC特征。计算MFCC的代码如下：

num_ceps = 13
mfcc = scipy.fftpack.dct(filter_banks, type=2, axis=1, norm='ortho')[:, :num_ceps]

# 绘制MFCC特征
plt.figure(figsize=(14, 5))
plt.title("MFCC")
plt.imshow(mfcc.T, aspect='auto', origin='lower')
plt.xlabel("Time (frames)")
plt.ylabel("MFCC Coefficients")
plt.colorbar()
plt.show()

通过这些步骤，我们可以详细地了解MFCC特征提取的过程及其每一步的效果。这些图示有助于更好地理解音频特征提取的工作原理。