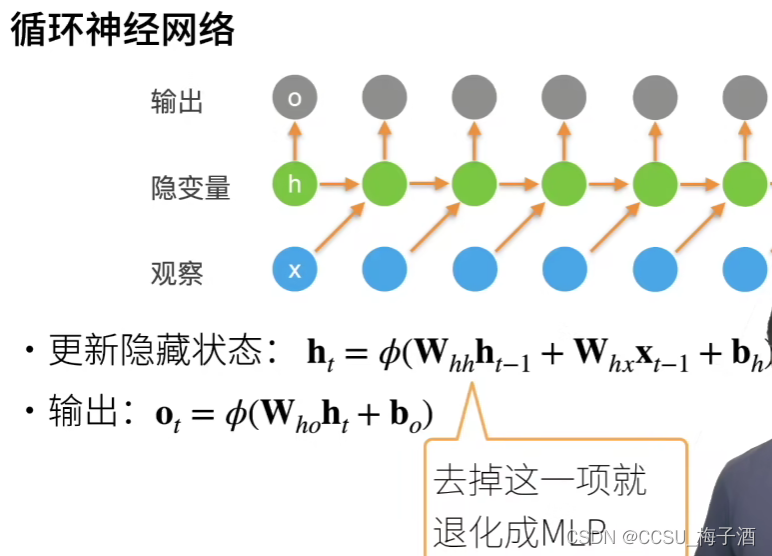
循环神经网络
在之前NLP基础章节-语言模型中我们介绍了
n
n
n 元语法,其中单词
x
t
x_t
xt 在时间步
t
t
t 的条件概率仅取决于前面
n
n
n 个单词,若是想要将之前单词的影响也加入那么模型参数数量会指数级增长。但是可能之前的单词存在重要的信息是无法舍弃的,于是我们可以参考NLP基础-序列模型中提到隐变量模型。
h
t
=
f
(
x
1
,
⋯
,
x
t
−
1
)
.
h_t = f(x_1,\cdots,x_{t-1}).
ht=f(x1,⋯,xt−1).
这样模型需要同时预测
x
t
x_t
xt 和更新
h
t
h_t
ht,于是模型形式上就变成:
h
t
=
g
(
h
t
−
1
,
x
t
−
1
)
.
h_t=g(h_{t-1},x_{t-1}).
ht=g(ht−1,xt−1).
x
t
=
P
(
x
t
∣
h
t
)
.
x_t=P(x_t|h_t).
xt=P(xt∣ht).
无隐状态的神经网络
无隐状态的神经网络其实可以看做多层感知机(MLP),回顾一下MLP的模型,设隐藏层的激活函数为
ϕ
\phi
ϕ,小批量样本为
X
X
X,隐藏层的输出
H
H
H 计算如下:(隐藏层并不等于隐变量)
H
=
ϕ
(
X
W
x
h
+
b
h
)
.
H = \phi(XW_{xh}+b_h).
H=ϕ(XWxh+bh). 接下来将隐藏层的输出
H
H
H 作为输出层的输入:
O
=
ϕ
(
H
W
h
q
+
b
q
)
.
O=\phi(HW_{hq}+b_{q}).
O=ϕ(HWhq+bq).
这样的模型我们已经很熟悉了。接下来看隐状态的神经网络。
有隐状态的神经网络
与多层感知机不同的是,我们需要保存前一个时间步的隐藏变量
H
t
−
1
H_{t-1}
Ht−1,并使用
W
h
h
W_{hh}
Whh 作为该隐变量的权重
H
t
=
ϕ
(
X
t
W
x
h
+
H
t
−
1
W
h
h
+
b
h
)
.
H_t=\phi(X_tW_{xh}+H_{t-1}W_{hh}+b_h).
Ht=ϕ(XtWxh+Ht−1Whh+bh).
O
t
=
H
t
W
h
q
+
b
q
.
O_t=H_tW_{hq}+b_q.
Ot=HtWhq+bq.
困惑度(Perplexity)
这里的困惑度是针对语言模型的质量的一个评分标准。一个好的语言模型能够用高度准确的词元来预测我们接下来会看到什么。 考虑一下由不同的语言模型给出的对“It is raining …”(“…下雨了”)的续写:
- “It is raining outside”(外面下雨了);
- “It is raining banana tree”(香蕉树下雨了);
- “It is raining piouw;kcj pwepoiut”(piouw;kcj pwepoiut下雨了)。
例1无疑是正确的,逻辑连贯符合情理的。而例2虽然正确拼写但句子没有逻辑没有意义。例3则根本没有正确的拼写。
根据信息论知识,如果想要压缩文本,我们可以根据当前词元集预测的下一个词元。 一个更好的语言模型应该能让我们更准确地预测下一个词元。 因此,它应该允许我们在压缩序列时花费更少的比特。 所以我们可以通过一个序列中所有的 n n n 个词元的交叉熵损失的平均值来衡量:
1 n ∑ t = 1 n − log P ( x t ∣ x t − 1 , ⋯ , x 1 ) \frac 1n\sum_{t=1}^{n}-\log P(x_t|x_{t-1},\cdots,x_1) n1t=1∑n−logP(xt∣xt−1,⋯,x1)
其中 P ( ) P() P() 由语言模型给出,而困惑度则是上式的指数:
exp ( − 1 n ∑ t = 1 n log P ( x t ∣ x t − 1 , ⋯ , x 1 ) ) \exp(-\frac 1n\sum_{t=1}^{n}\log P(x_t|x_{t-1},\cdots,x_1)) exp(−n1t=1∑nlogP(xt∣xt−1,⋯,x1))
困惑度的最好的理解是“下一个词元的实际选择数的调和平均数”。