第三章 对数几率回归

3.1 算法原理

对数几率回归（Logistic Regression）是一种统计方法，主要用于二分类问题。它通过拟合一个对数几率函数（logit function），即对数几率（log-odds）与输入变量的线性组合之间的关系，来预测一个事件发生的概率。其基本公式为：
$$logit(P)=ln(\frac{P}{1-P})={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+...+{\beta }_n{X}_n$$
其中，P是事件发生的概率，${\beta }_0$是截距，${\beta }_1,{\beta }_2,...,{\beta }_n$是回归系数，$X_1,X_2,...,X_n$是输入变量。通过对参数$\beta$进行估计，模型可以用于预测新数据点的分类结果。
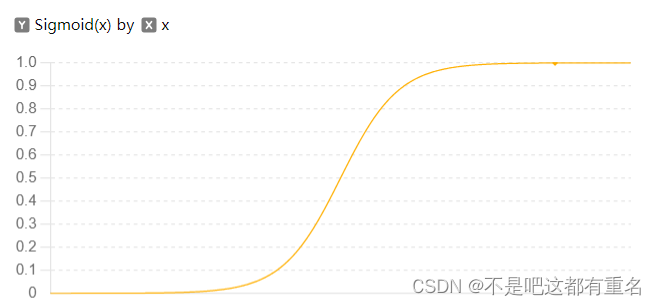
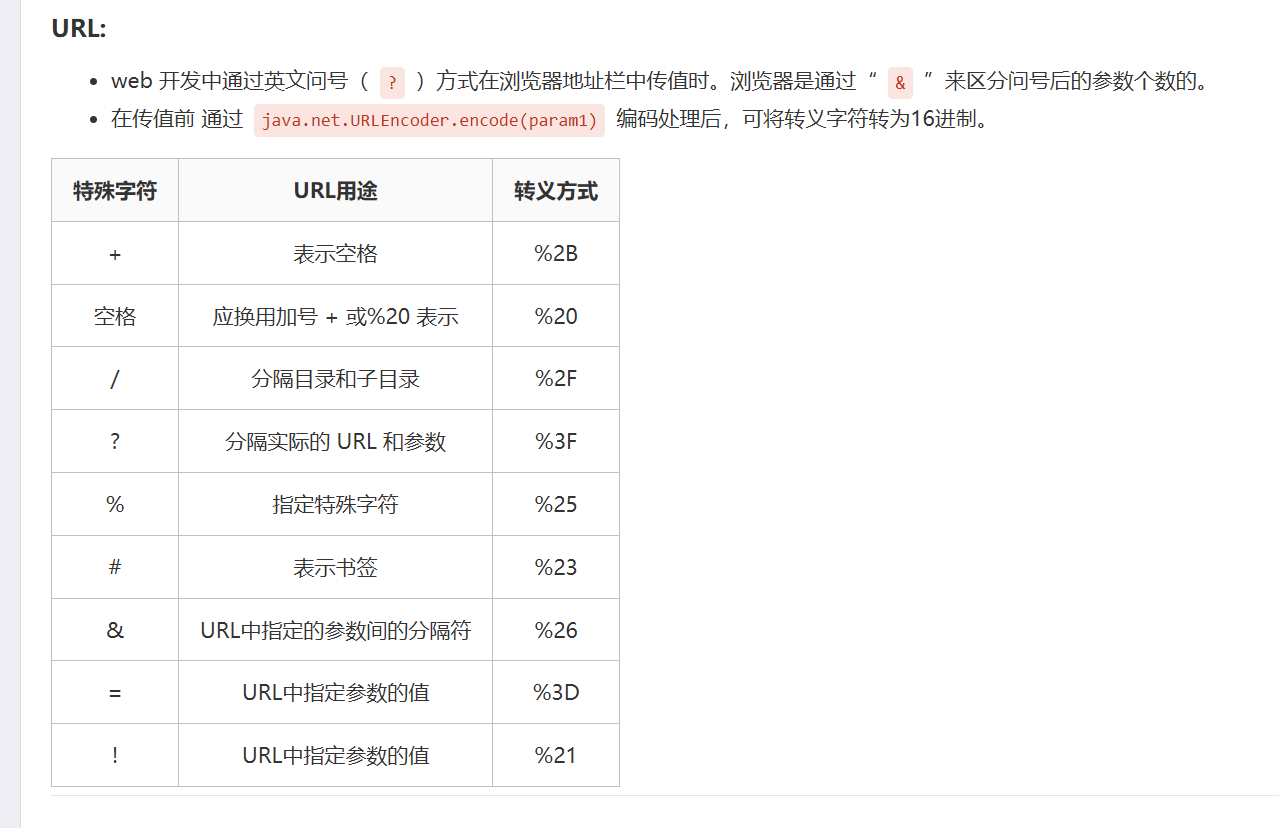
简单来说，它是在线性模型的基础上套了一个映射函数来实现分类功能，在这里是套了一个$\frac{1}{1+e^{-z}}$函数，其图像如下图所示:

3.2损失函数的极大似然估计推导（策略）

第一步： 确定概率质量函数（质量密度函数）
已知离散型随机变量 y ∈ { 0 , 1 } y\in{\{0,1\}} y∈{0,1}取值为1和0的概率分别建模为：
$$p(y=1|x)=\frac{1}{1+e^{-(w^{T}x+b)}}=\frac{e^{w^{T}x+b}}{1+e^{w^{T}x+b}}$$
$$p(y=0|x)=1-p(y=1|x)=\frac{1}{1+e^{w^{T}x+b}}$$
通过以上概率取值可推得随机变量 y ∈ { 0 , 1 } y\in{\{0,1\}} y∈{0,1}的概率质量函数为
$$p(y|\hat{x};\beta )=y\cdot p_1(\hat{x};\beta )+(1-y)\cdot p_0(\hat{x};\beta )$$
另一种表达是，
$$p(y|\hat{x};\beta )=[p_1(\hat{x};\beta ){]}^y+[p_0(\hat{x};\beta ){]}^{1-y}$$
第二步： 写出似然函数
$$L(\beta )=\prod _{i=1}^{m}p(y_i|{\hat{x}}_i;\beta )$$
对数似然函数为
$$l(\beta )=lnL(\beta )=\sum _{i=1}^{m}p(y_i|{\hat{x}}_i;\beta )$$
$$l(\beta )=\sum _{i=1}^{m}ln(y_i{p}_1({\hat{x}}_i;\beta )+(1-y_i)p_0({\hat{x}}_i;\beta ))$$
带入化简得：
$$l(\beta )=\sum _{i=1}^m(y_i{\beta }^T{\hat{x}}_i-ln(1+e^{{\beta }^T{\hat{x}}_i}))$$
最后取反即得到西瓜书得式（3.27），即对小化损失函数。

3.3损失函数的信息论推导（策略）

信息论（Information Theory）是一门研究信息的度量、传输和处理的科学。它由克劳德·香农（Claude Shannon）在20世纪中期创立。信息论的应用广泛，包括数据压缩、加密、通信系统设计、机器学习等领域。通过量化信息和不确定性，信息论为理解和优化信息处理系统提供了理论基础。
关键概念：
1.自信息：在信息论中，自信息（Self-Information），又称为信息量或惊讶度，是一个度量事件不确定性的概念。自信息量用于描述单个事件的置信度或信息含量。其定义如下：
$$I(x)=-logP(x)$$
其中，I（x）是事件x的自信息量，P（x）是事件x发生的概率，log 表示对数运算，可以是以2为底（通常用于信息论中的单位为比特）或以自然对数为底（单位为纳特，nats）。
2.信息熵（Entropy）是信息论中的一个核心概念，用来衡量一个随机变量的不确定性或信息量。它是由克劳德·香农（Claude Shannon）在其1948年的论文《通信的数学理论》中提出的，因此有时也称为香农熵。信息熵的定义如下：
$$H(X)=-\sum _{i}P(x_i)logP(x_i)$$
其中：
$H(X)$是随机变量X的熵；
$P(x_i)$是随机变量X取值为$x_i$的概率。
log是对数运算
要注意的一点是，当$p(x)=0$,则$p(x)lo{g}_{b}p(x)=0$
3.相对熵（Relative Entropy），也称为Kullback-Leibler散度（Kullback-Leibler Divergence, 简称KL散度），是信息论中用来衡量两个概率分布之间差异的非对称度量。它描述了从一个分布到另一个分布的额外信息量或“代价”。相对熵的定义如下：
对于两个概率分布P和Q，相对熵$D_{KL}(P||Q)$定义为：
$$D_{KL}(P||Q)=\sum _{x\in \mathcal{X}}P(x)log\frac{P(x)}{Q(x)}$$
其中，
P和Q是定义在同一随机变量X上的两个概率分布;
$\mathcal{X}$是X的取值范围;
log是对数运算。
上面的式子可以化为：
$$D_{KL}(p||q)=\sum _{x}p(x)logp(x)-\sum _{x}p(x)lo{g}_{b}q(x)$$
可以看到上面的式子的后半部分就是交叉熵。由于理想分布p(x)是未知但固定的分布（频率学派的角度），所以式子的前办部分是一个常量，那么最小化相对熵就等价于最小化交叉熵。
以对数几率回归为例，对单个样本$y_i$来说，它的理想分布是
$$p(y_i)=\{\begin{array}{r}p(1)=1,p(0)=0,y_i=1\\ p(1)=0,p(0)=1,y_i=0\end{array}$$
模拟分布为：
$$q(y_i)=\{\begin{array}{r}\frac{e^{{\beta }^T\hat{x}}}{1+e^{{\beta }^T\hat{x}}}=p_1(\hat{x};\beta ),y_i=1\\ \frac{1}{1+e^{{\beta }^T\hat{x}}}=p_0(\hat{x};\beta ),y_i=0\end{array}$$
带入交叉熵公式同时全体训练样本的交叉熵求和化简得到，
$$\sum _{i=1}^m(-y_i{\beta }^T{\hat{x}}_i+ln(1+e^{{\beta }^T{\hat{x}}_i}))$$

3.4补充

对数几率回归算法的机器学习三要素：
1.模型：线性模型，输出值得范围为[0，1],近似阶跃得单调可微函数
2.策略：极大似然估计，信息论
3.算法：梯度下降，牛顿法（近似求解方法，没有闭式解）