C++——布隆过滤器

news2024/11/22 16:39:45

目录

布隆过滤器的提出

布隆过滤器的概念

布隆过滤器的基本原理和特点

布隆过滤器的实现

 布隆过滤器的插入

布隆过滤器的查找

 布隆过滤器的删除

布隆过滤器的优点

布隆过滤器的缺陷

布隆过滤器使用场景

布隆过滤器的提出

在注册账号设置昵称的时候，为了保证每个用户昵称的唯一性，系统必须检测你输入的昵称是否被使用过，这本质就是一个key的模型，我们只需要判断这个昵称被用过，还是没被用过。

方法一：用红黑树或哈希表将所有使用过的昵称存储起来，当需要判断一个昵称是否被用过时，直接判断该昵称是否在红黑树或哈希表中即可。但红黑树和哈希表最大的问题就是浪费空间，当昵称数量非常多的时候内存当中根本无法存储这些昵称
方法二：用位图将所有使用过的昵称存储起来，虽然位图只能存储整型数据，但我们可以通过一些哈希算法将字符串转换成整型，比如BKDR哈希算法。当需要判断一个昵称是否被用过时，直接判断位图中该昵称对应的比特位是否被设置即可。
位图虽然能够大大节省内存空间，但由于字符串的组合形式太多了，一个字符的取值有256种，而一个数字的取值只有10种，因此无论通过何种哈希算法将字符串转换成整型都不可避免会存在哈希冲突。

这里的哈希冲突就是不同的昵称最终被转换成了相同的整型，此时就可能会引发误判，即某个昵称明明没有被使用过，却被系统判定为已经使用过了，于是就出现了布隆过滤器。

布隆过滤器的概念

布隆过滤器是由布隆（Burton Howard Bloom）在1970年提出的一种紧凑型的、比较巧妙的概率型数据结构，特点是高效地插入和查询。

1.布隆过滤器其实就是位图的一个变形和延申，虽然无法避免存在哈希冲突，但我们可以想办法降低误判的概率。
2.当一个数据映射到位图中时，布隆过滤器会用多个哈希函数将其映射到多个比特位，当判断一个数据是否在位图当中时，需要分别根据这些哈希函数计算出对应的比特位，如果这些比特位都被设置为1则判定为该数据存在，否则则判定为该数据不存在。
3.布隆过滤器使用多个哈希函数进行映射，目的就在于降低哈希冲突的概率，一个哈希函数产生冲突的概率可能比较大，但多个哈希函数同时产生冲突的概率可就没那么大了。


假设布隆过滤器使用三个哈希函数进行映射，那么“张三”这个昵称被使用后位图中会有三个比特位会被置1，当有人要使用“李四”这个昵称时，就算前两个哈希函数计算出来的位置都产生了冲突，但由于第三个哈希函数计算出的比特位的值为0，此时系统就会判定“李四”这个昵称没有被使用过。

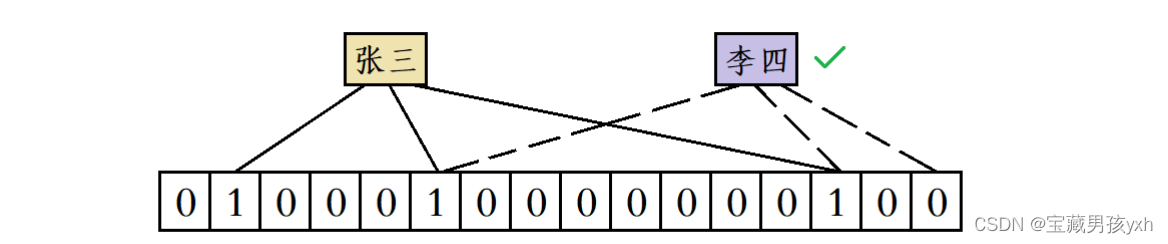
但随着位图中添加的数据不断增多，位图中1的个数也在不断增多，此时就会导致误判的概率增加。

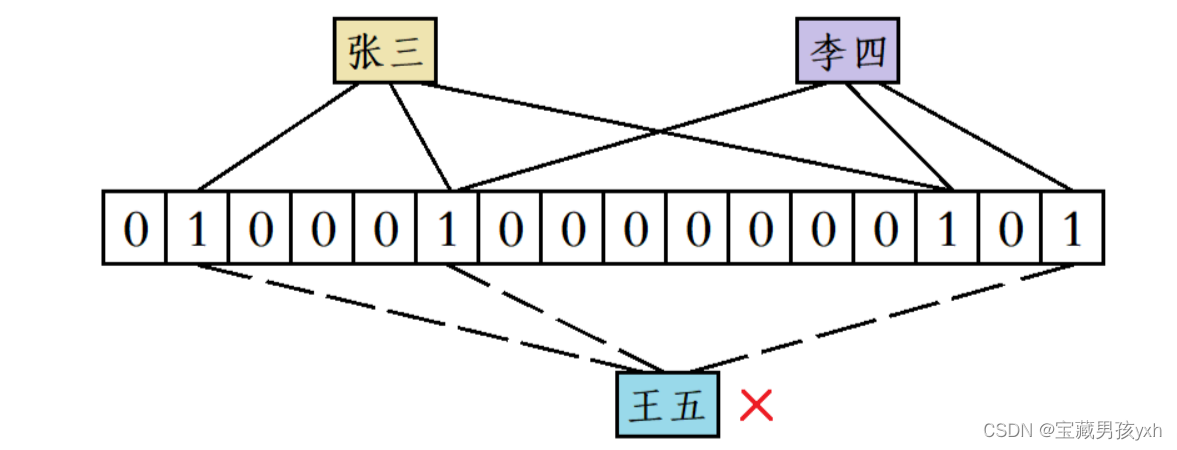
比如“张三”和“李四”都添加到位图中后，当有人要使用“王五”这个昵称时，虽然“王五”计算出来的三个位置既不和“张三”完全一样，也不和“李四”完全一样，但“王五”计算出来的三个位置分别被“张三”和“李四”占用了，此时系统也会误判为“王五”这个昵称已经被使用过了。

布隆过滤器的基本原理和特点

  1. 数据结构：

    • 位数组（Bit Array）：通常是一个很长的二进制向量，初始时所有位都被置为0。
    • 多个哈希函数：通常选择多个独立的哈希函数，每个哈希函数能够将任意元素映射到位数组中的一个位上。

  2. 插入元素：

    • 当向布隆过滤器中插入一个元素时，使用多个哈希函数计算元素的哈希值，并将对应的位数组中的位置置为1。

  3. 查询元素：

    • 当查询一个元素是否在布隆过滤器中时，同样使用多个哈希函数计算元素的哈希值，并检查对应的位数组中的位置是否都为1。
    • 如果所有对应的位都为1，则说明该元素可能在集合中；如果有任何一个位为0，则该元素肯定不在集合中。

  4. 特点：

    • 空间效率高：布隆过滤器只需要使用很少的额外空间来存储数据，主要是位数组和哈希函数。
    • 查询时间快：查询一个元素的时间复杂度是常数时间，因为只需进行固定次数的位操作和哈希计算。
    • 可能存在误判：由于多个元素可能映射到同一位置，所以布隆过滤器存在一定的误判率，即可能判断一个元素在集合中但实际上不在（false positive）。

如何控制误判率 

很显然，过小的布隆过滤器很快所有的比特位都会被设置为1，此时布隆过滤器的误判率就会变得很高，因此布隆过滤器的长度会直接影响误判率，布隆过滤器的长度越长其误判率越小。
此外，哈希函数的个数也需要权衡，哈希函数的个数越多布隆过滤器中比特位被设置为1的速度越快，并且布隆过滤器的效率越低，但如果哈希函数的个数太少，也会导致误判率变高。

其中k为哈希函数个数，m为布隆过滤器长度，n为插入的元素个数，p为误判率。

我们这里可以大概估算一下，如果使用3个哈希函数，即k的值为3，l n 2 ln2ln2的值我们取0.7，那么 m mm 和 n nn 的关系大概是m = 4 × n m=4\times nm=4×n，也就是布隆过滤器的长度应该是插入元素个数的4倍。

布隆过滤器的实现

首先，布隆过滤器可以实现为一个模板类，因为插入布隆过滤器的元素不仅仅是字符串，也可以是其他类型的数据，只有调用者能够提供对应的哈希函数将该类型的数据转换成整型即可，但一般情况下布隆过滤器都是用来处理字符串的，所以这里可以将模板参数K的缺省类型设置为string。

布隆过滤器中的成员一般也就是一个位图，我们可以在布隆过滤器这里设置一个非类型模板参数N，用于让调用者指定位图的长度。

//布隆过滤器
template<size_t N, class K = string, class Hash1 = BKDRHash, class Hash2 = APHash, class Hash3 = DJBHash>
class BloomFilter
{
public:
	//...
private:
	bitset<N> _bs;
};

实例化布隆过滤器时需要调用者提供三个哈希函数，由于布隆过滤器一般处理的是字符串类型的数据，因此这里我们可以默认提供几个将字符串转换成整型的哈希函数。

这里选取将字符串转换成整型的哈希函数，是经过测试后综合评分最高的BKDRHash、APHash和DJBHash，这三种哈希算法在多种场景下产生哈希冲突的概率是最小的。
此时本来这三种哈希函数单独使用时产生冲突的概率就比较小，现在要让它们同时产生冲突概率就更小了。
代码如下：

struct BKDRHash
{
	size_t operator()(const string& s)
	{
		size_t value = 0;
		for (auto ch : s)
		{
			value = value * 131 + ch;
		}
		return value;
	}
};
struct APHash
{
	size_t operator()(const string& s)
	{
		size_t value = 0;
		for (size_t i = 0; i < s.size(); i++)
		{
			if ((i & 1) == 0)
			{
				value ^= ((value << 7) ^ s[i] ^ (value >> 3));
			}
			else
			{
				value ^= (~((value << 11) ^ s[i] ^ (value >> 5)));
			}
		}
		return value;
	}
};
struct DJBHash
{
	size_t operator()(const string& s)
	{
		if (s.empty())
			return 0;
		size_t value = 5381;
		for (auto ch : s)
		{
			value += (value << 5) + ch;
		}
		return value;
	}
};

 布隆过滤器的插入

布隆过滤器当中需要提供一个Set接口，用于插入元素到布隆过滤器当中。插入元素时，需要通过三个哈希函数分别计算出该元素对应的三个比特位，然后将位图中的这三个比特位设置为1即可。

代码如下：

void Set(const K& key)
{
	//计算出key对应的三个位
	size_t i1 = Hash1()(key) % N;
	size_t i2 = Hash2()(key) % N;
	size_t i3 = Hash3()(key) % N;

	//设置位图中的这三个位
	_bs.set(i1);
	_bs.set(i2);
	_bs.set(i3);
}

布隆过滤器的查找

布隆过滤器当中还需要提供一个Test接口，用于检测某个元素是否在布隆过滤器当中。检测时，需要通过三个哈希函数分别计算出该元素对应的三个比特位，然后判断位图中的这三个比特位是否被设置为1。

只要这三个比特位当中有一个比特位未被设置则说明该元素一定不存在。
如果这三个比特位全部被设置，则返回true表示该元素存在（可能存在误判）。
代码如下：

bool Test(const K& key)
{
	//依次判断key对应的三个位是否被设置
	size_t i1 = Hash1()(key) % N;
	if (_bs.test(i1) == false)
	{
		return false; //key一定不存在
	}

	size_t i2 = Hash2()(key) % N;
	if (_bs.test(i2) == false)
	{
		return false; //key一定不存在
	}

	size_t i3 = Hash3()(key) % N;
	if (_bs.test(i3) == false)
	{
		return false; //key一定不存在
	}

	return true; //key对应的三个位都被设置，key存在（可能误判）
}

 布隆过滤器的删除

布隆过滤器一般不支持删除操作，原因如下：

因为布隆过滤器判断一个元素存在时可能存在误判，因此无法保证要删除的元素确实在布隆过滤器当中，此时将位图中对应的比特位清0会影响其他元素。
此外，就算要删除的元素确实在布隆过滤器当中，也可能该元素映射的多个比特位当中有些比特位是与其他元素共用的，此时将这些比特位清0也会影响其他元素。

如何让布隆过滤器支持删除？

要让布隆过滤器支持删除，必须要做到以下两点：

1.保证要删除的元素在布隆过滤器当中。比如刚才的呢称例子当中，如果通过调用Test函数得知要删除的昵称可能存在布隆过滤器当中后，可以进一步遍历存储昵称的文件，确认该昵称是否真正存在。
2.保证删除后不会影响到其他元素。可以为位图中的每一个比特位设置一个对应的计数值，当插入元素映射到该比特位时将该比特位的计数值++，当删除元素时将该元素对应比特位的计数值–即可。
可是布隆过滤器最终还是没有提供删除的接口，因为使用布隆过滤器本来就是要节省空间和提高效率的。在删除时需要遍历文件或磁盘中确认待删除元素确实存在，而文件IO和磁盘IO的速度相对内存来说是很慢的，并且为位图中的每个比特位额外设置一个计数器，就需要多用原位图几倍的存储空间，这个代价也是不小的。

布隆过滤器的优点

  1. 空间效率高：

    • 布隆过滤器利用位数组和多个哈希函数来表示数据集合，相比于其他数据结构（如哈希表），它通常占用更少的存储空间。这是因为位数组通常只需要存储每个元素的部分信息（即位），而不需要存储完整的元素本身。

  2. 插入和查询速度快：

    • 插入元素时，布隆过滤器只需要计算几个哈希函数的值并设置对应位的操作，时间复杂度是常数级别的（O(k)，其中 k 是哈希函数的数量）。
    • 查询元素时，同样只需计算几个哈希函数的值并检查对应位的状态，也是常数时间复杂度的操作。

  3. 支持大规模数据：

    • 布隆过滤器适合处理大规模数据集合，因为它的插入和查询操作都具有较快的时间复杂度，并且可以通过调整位数组的大小和哈希函数的数量来适应不同规模的数据集合。

  4. 低误判率：

    • 在正确使用的情况下，布隆过滤器可以控制误判率，即尽管可能会有少量的误判（false positive），但可以通过合理选择哈希函数数量和位数组大小来将误判率降到较低水平。

  5. 无需存储完整数据：

    • 布隆过滤器存储的是数据的部分信息（即哈希值对应的位），而不需要存储完整的数据本身。这在存储敏感或大规模数据时尤为重要，可以节省大量的存储空间。

  6. 简单高效：

    • 布隆过滤器的实现相对简单，只需要实现位数组和哈希函数即可，没有复杂的数据结构或算法。这使得布隆过滤器易于理解和部署。

总之，布隆过滤器在需要快速插入和查询大规模数据集合，并且可以接受一定误判率的场景中，是一种高效且经济的选择。

布隆过滤器的缺陷

然布隆过滤器在很多场景下有着显著的优点，但它也有一些明显的缺陷，需要在使用时进行考虑和权衡：

  1. 存在误判（False Positive）：

    • 布隆过滤器在判断一个元素是否存在时，有可能会出现误判，即判断一个元素存在于集合中，但实际上并不存在（false positive）。这是因为多个元素可能映射到位数组中的同一个位上，导致该位被置为1，从而误判其他元素也存在。

  2. 不支持删除操作：

    • 布隆过滤器一般不支持删除元素操作。由于元素的存在信息可能被多个元素共享，删除一个元素会影响其他元素的判断结果。即使可以进行删除，也需要额外的设计和实现来保证正确性，增加了复杂性和开销。

  3. 无法准确判断元素个数：

    • 布隆过滤器只能统计有多少个位被置为1，而无法准确地计算实际元素的个数。这对于一些应用场景（如需要精确统计元素个数的情况）可能是一个限制。

  4. 哈希函数的选择和设计：

    • 布隆过滤器的性能和误判率与选择的哈希函数密切相关。如果选择的哈希函数不足够独立或者没有良好设计，可能会导致误判率增加或者性能下降。

  5. 空间消耗和位数组大小：

    • 虽然布隆过滤器在空间效率上比较高效，但其需要的存储空间和位数组的大小取决于期望的误判率和要处理的元素数量。在需要较低误判率的情况下，可能需要更大的位数组，增加了空间消耗。

  6. 性能随负载增加而变化：

    • 随着插入元素数量的增加，布隆过滤器的性能可能会受到影响。特别是当位数组中的大多数位已经被置为1时，误判率可能会显著增加，查询性能也可能下降。

  7. 不适用于所有场景：

    • 布隆过滤器适合于那些可以容忍一定误判率的应用场景。对于一些要求高精度和不能容忍误判的场景，布隆过滤器可能不适用。

综上所述，虽然布隆过滤器在特定的应用场景下表现优异，但在使用时需要注意其误判率、不支持删除等缺陷，并根据具体需求进行合理的选择和使用。

布隆过滤器使用场景

布隆过滤器（Bloom Filter）由于其高效的插入和查询操作以及较低的空间需求，适用于多种实际场景，特别是在需要快速判断某个元素是否可能存在于一个大集合中的情况下。以下是一些布隆过滤器常见的使用场景：

  1. 缓存和数据预取：

    • 在缓存系统中，布隆过滤器可以用来快速判断一个请求的内容是否在缓存中。如果布隆过滤器判断内容不在缓存中（即不存在），可以避免进行昂贵的数据库或网络请求，从而提高系统的响应速度和性能。

  2. 垃圾邮件过滤：

    • 在垃圾邮件过滤系统中，布隆过滤器可以用来存储已知的垃圾邮件特征或发送者信息。当新的邮件到达时，可以通过布隆过滤器快速判断该邮件是否属于已知的垃圾邮件类型，从而进行快速过滤。

  3. 网络爬虫去重：

    • 在网络爬虫系统中，布隆过滤器可以用来避免重复抓取同一个URL。爬虫在抓取新的网页时，可以先通过布隆过滤器判断URL是否已经被抓取过，避免重复下载同一个页面。

  4. 集合成员检测：

    • 在分布式系统或者大规模数据处理中，布隆过滤器可以用来快速检查一个元素是否存在于一个庞大的数据集合中，如分布式数据库或者分布式缓存中。这可以减少网络通信和查询时间，提高系统效率。

  5. 防止缓存穿透：

    • 布隆过滤器可以用于防止缓存穿透问题，即恶意请求多次查询一个不存在的内容，导致缓存系统频繁失效。通过布隆过滤器预先判断请求的内容是否可能存在，可以有效减少无效查询对系统的影响。

  6. 安全性应用：

    • 在安全领域，布隆过滤器可以用于快速查找恶意IP地址、URL或者文件哈希值等，帮助进行快速的安全检测和阻断。

  7. 大数据处理：

    • 在大数据处理中，布隆过滤器可以用来过滤掉不可能存在的数据项，从而减少对庞大数据集的处理负担和提高处理效率。

总之，布隆过滤器在需要快速、高效地判断元素是否可能存在于一个集合中，并且可以容忍一定的误判率的应用场景下，是一种非常有用的数据结构工具。通过合理的使用和参数配置，可以在很多实际问题中发挥重要作用。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1862716.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

word文档怎么加密？电脑文件加密的详细步骤【分享4个】

word文档怎么加密？电脑文件加密的详细步骤【分享4个】

为了保护Word文档不被未经授权的人员访问或修改&#xff0c;我们通常会采用加密的方式来增加其安全性。那么Word文档怎么加密&#xff1f;电脑文档安全成为了大家所关心的话题。 本文针对不同的情况&#xff0c;本文分享了4种电脑文件加密的方法&#xff0c;每一种加密方法都比…
阅读更多...
数据分析必备：一步步教你如何用matplotlib做数据可视化（12）

数据分析必备：一步步教你如何用matplotlib做数据可视化（12）

1、Matplotlib 3D线框图 线框图采用值网格并将其投影到指定的三维表面上&#xff0c;并且可以使得到的三维形式非常容易可视化。plot_wireframe()函数用于此目的 import matplotlib.pyplot as plt import numpy as np import math import seaborn as sns plt.rcParams[font.s…
阅读更多...
ArkTS自定义组件

ArkTS自定义组件

一、自定义组件基本结构 // 定义自定义组件 ButtonCom.ets Component export struct BtnCom{State msg: string "按钮";build() {Row(){Text(this.msg).onClick(() > {this.msg "测试"})}} } // 引入自定义组件 import {BtnCom} from "./Butto…
阅读更多...
MySQL——联表查询JoinON详解

MySQL——联表查询JoinON详解

Join 对比&#xff08;7种&#xff09; 代码演示&#xff1a; -- 查询参加了考试的同学&#xff08;学号&#xff0c;姓名&#xff0c;科目编号&#xff0c;分数&#xff09; SELECT * FROM student SELECT * FROM result/* 1. 分析需求&#xff1a;分析查询的字段来自哪些表&…
阅读更多...
Ubuntu安装NVIDIA驱动

Ubuntu安装NVIDIA驱动

目录 安装gcc 安装NVIDIA驱动 检查nvidia显卡型号 根据显卡型号下载对应的驱动 安装命令 如何卸载 安装gcc 安装显卡驱动需要使用gcc&#xff0c;输入命令检查是否有gcc gcc --version 如果有版本号弹出&#xff0c;说明已经有gcc环境了&#xff0c;没有的则运行以下…
阅读更多...
【高校科研前沿】四川大学刘超研究员为一作在《Geophys. Res. Lett.》发表团队成果：植被形态影响河床泥沙输运

【高校科研前沿】四川大学刘超研究员为一作在《Geophys. Res. Lett.》发表团队成果：植被形态影响河床泥沙输运

文章简介 论文名称&#xff1a;Plant morphology impacts bedload sediment transport 第一作者及单位&#xff1a;刘超&#xff08;研究员|四川大学水利水电学院&#xff09; 通讯作者及单位&#xff1a;Yuqi Shan&#xff08;四川大学灾后重建与管理研究所&#xff09; 文…
阅读更多...
Kafka基本架构

Kafka基本架构

「kafka设计思想」 一个最基本的架构是生产者发布一个消息到Kafka的一个Topic &#xff0c;该Topic的消息存放于的Broker中&#xff0c;消费者订阅这个Topic&#xff0c;然后从Broker中消费消息&#xff0c;下面这个图可以更直观的描述这个场景&#xff1a; 「消息状态&#x…
阅读更多...
C++初学者指南-2.输入和输出---文件输入和输出

C++初学者指南-2.输入和输出---文件输入和输出

C初学者指南-2.输入和输出—文件输入和输出 文章目录 C初学者指南-2.输入和输出---文件输入和输出1.写文本文件2.读文本文件3.打开关闭文件4.文件打开的模式 1.写文本文件 使用&#xff1a; std::ofstream&#xff08;输出文件流&#xff09; #include <fstream> // 文…
阅读更多...
2024.6.25力扣刷题记录-周赛403

2024.6.25力扣刷题记录-周赛403

目录 一、3194. 最小元素和最大元素的最小平均值 二、3195. 包含所有 1 的最小矩形面积 I 三、3196. 最大化子数组的总成本 四、3197. 包含所有 1 的最小矩形面积 II 博主在比赛时只过了前两题。剩下跟着灵神做&#xff0c;来自视频&#xff1a; 【状态机 DP【力扣周赛 403…
阅读更多...
dwg文件转换的软件，分享4款软件！

dwg文件转换的软件，分享4款软件！

在数字化设计领域&#xff0c;DWG文件作为CAD&#xff08;计算机辅助设计&#xff09;的核心文件格式&#xff0c;其重要性不言而喻。然而&#xff0c;在实际应用中&#xff0c;我们有时需要将DWG文件转换为其他格式以便于分享、展示或进行其他操作。那么&#xff0c;DWG文件转…
阅读更多...
vue3，pinia状态管理，手写插件实现持久化

vue3，pinia状态管理，手写插件实现持久化

状态管理和持久化 先简单概述一下状态管理和持久化 状态管理&#xff1a;使任意两个组件共享数据持久化&#xff1a;将共享的数据保存在本地&#xff0c;不随页面销毁而消失 要实现状态的持久化&#xff0c;可以直接采用插件的形式实现&#xff0c;插件其实就是一个函数&#…
阅读更多...
民生银行北京分行金融科技校招面试记录

民生银行北京分行金融科技校招面试记录

本文介绍2024届春招中&#xff0c;中国民生银行下属北京分行的金融科技岗位1场面试的基本情况、提问问题等。 2024年04月投递了中国民生银行下属北京分行的金融科技岗位&#xff0c;暂时不清楚所在部门。目前完成了一面与终面&#xff0c;在这里记录一下面试的相关经历。 首先&…
阅读更多...
UFS协议—新手快速入门（四）【10】

UFS协议—新手快速入门（四）【10】

目录 十、UPIU数据包格式详解 1、Transaction Type&#xff08;类型&#xff09; 2、Flags&#xff08;附加信息&#xff09; 其它 3、LUN&#xff08;逻辑单元号&#xff09;&#xff1a; 4、Task Tag&#xff08;任务标签&#xff09;&#xff1a; 5、Command Type&…
阅读更多...
你还不知道Modbus RTU???

你还不知道Modbus RTU???

1. 什么是Modbus RTU Modbus RTU&#xff08;Remote Terminal Unit&#xff09;是Modbus通信协议的一种变种&#xff0c;用于串行通信。它是一种常见的工业控制系统通信协议&#xff0c;通常用于采集传感器数据、控制执行器和监控设备状态。Modbus RTU采用二进制编码&#xff0…
阅读更多...
突破Web3红海，DePIN如何构建创新生态系统？

突破Web3红海，DePIN如何构建创新生态系统？

撰文&#xff1a;TinTinLand 本文来源香港Web3媒体Techub News专栏作者TinTinLand 2023 年 DePIN 赛道的火热成为 Web3 行业的重点关注方向&#xff0c;当前如何以可扩展、去中心化、安全方式推动 DePIN 赛道赋能下的 AI 版图建设&#xff0c;寻找更多 Web3 行业创新机遇成为…
阅读更多...
静电场的基本方程

静电场的基本方程

目录 场积分方程 通量&#xff08;高斯定理&#xff09; 环量 场微分方程 散度 旋度 小结 补充知识 立体角 场积分方程 通量&#xff08;高斯定理&#xff09; 环量 场微分方程 散度 旋度 小结 补充知识 立体角
阅读更多...
打开自动联网，设置静态IP

打开自动联网，设置静态IP

TYPEEthernet PROXY_METHODnone BROWSER_ONLYno BOOTPROTOstatic # 设置为static DEFROUTEyes IPV4_FAILURE_FATALno IPV6INITyes IPV6_AUTOCONFyes IPV6_DEFROUTEyes IPV6_FAILURE_FATALno IPV6_ADDR_GEN_MODEstable-privacy NAMEens18 UUIDce34dd13-05cb-4d6d-95e4-252355b1…
阅读更多...
c++网络通信

c++网络通信

TCP/IP协议 OSI参考模型采用分层划分原则&#xff0c;将网络中的数据传输划分为7层&#xff0c;其中&#xff0c;物理层居于最下层&#xff0c;是最基础、核心的网络硬件层&#xff1b;应用层居于最上层&#xff0c;负责应用资源的管理。每一层使用下层的服务&#xff0c;并向…
阅读更多...
内存卡数据移走了怎样恢复？简易步骤与解决方案

内存卡数据移走了怎样恢复？简易步骤与解决方案

随着科技的快速发展&#xff0c;内存卡已成为我们日常生活中不可或缺的一部分&#xff0c;特别是在行车记录仪、手机、相机等设备上。然而&#xff0c;当内存卡中的数据意外移走或删除时&#xff0c;我们往往会感到焦虑和困惑。本文将为您介绍如何简易恢复内存卡中移走的数据&a…
阅读更多...
[leetcode]valid-triangle-number. 有效三角形的个数

[leetcode]valid-triangle-number. 有效三角形的个数

. - 力扣&#xff08;LeetCode&#xff09; class Solution { public:int triangleNumber(vector<int>& nums) {int n nums.size();sort(nums.begin(), nums.end());int ans 0;for (int i 0; i < n; i) {for (int j i 1; j < n; j) {int left j 1, righ…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023