线性判别分析

线性判别分析（Linear Discriminant Analysis，LDA）亦称 Fisher 判别分析。其基本思想是：将训练样本投影到低维超平面上，使得同类的样例尽可能近，不同类的样例尽可能远。在对新样本进行分类时，将其投影到同样的超平面上，再根据投影点的位置来确定新样本的类别。

给定的数据集
$$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),\cdots ,({\mathbf{x}}_N,y_N)\}$$
包含 $N$ 个样本，$p$ 个特征。其中，第 $i$ 个样本的特征向量为 ${\mathbf{x}}_i=(x_{i1},x_{i2},\cdots ,x_{ip}{)}^T$ 。目标变量 y i ∈ { c 1 , c 2 , ⋯   , c K } y_i\in \{c_1,c_2,\cdots,c_K\} yi​∈{c1​,c2​,⋯,cK​} 。

二分类

我们先定义$N_k$为第 $k$ 类样本的个数
$$\sum _{k=1}^K{N}_k=N$$
${\mathcal{X}}_k$为第 $k$ 类样本的特征集合
X k = { x ∣ y = c k ,   ( x , y ) ∈ D } \mathcal X_k=\{\mathbf x | y=c_k,\ (\mathbf x,y)\in D \} Xk​={x∣y=ck​, (x,y)∈D}

${\mu }_k$为第 $k$ 类样本均值向量
$${\mu }_k=\frac{1}{N_k}\sum _{\mathbf{x}\in {\mathcal{X}}_k}\mathbf{x}$$

${\Sigma }_k$为第 $k$ 类样本协方差矩阵
$${\Sigma }_k=\frac{1}{N_k}\sum _{\mathbf{x}\in {\mathcal{X}}_k}(\mathbf{x}-{\mu }_k)(\mathbf{x}-{\mu }_k{)}^T$$

首先从比较简单的二分类为例 y ∈ { 0 , 1 } y\in \{0,1\} y∈{0,1}，若将数据投影到直线 $\mathbf{w}$ 上，则对任意一点 $\mathbf{x}$，它在直线 $\mathbf{w}$ 的投影为 ${\mathbf{w}}^T\mathbf{x}$ ¹。

• LDA需要让不同类别的数据的类别中心之间的距离尽可能的大，也就是要最大化 $\Vert {\mathbf{w}}^T{\mu }_0-{\mathbf{w}}^T{\mu }_1{\Vert }_2^2$；
• 同时希望同一种类别数据的投影点尽可能的接近，也就是要同类样本投影点的方差最小化 ${\mathbf{w}}^T{\Sigma }_0\mathbf{w}+{\mathbf{w}}^T{\Sigma }_1\mathbf{w}$。

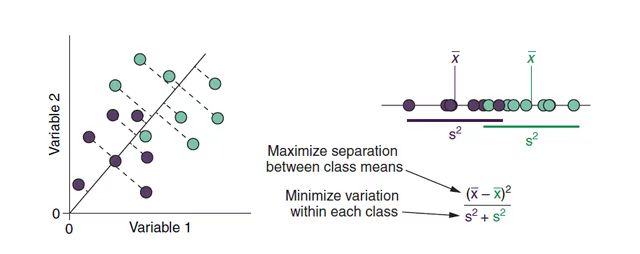
综上所述，我们的优化目标为：
$$\underset{\mathbf{w}}{\max }\frac{\Vert {\mathbf{w}}^T{\mu }_0-{\mathbf{w}}^T{\mu }_1{\Vert }_2^2}{{\mathbf{w}}^T{\Sigma }_0\mathbf{w}+{\mathbf{w}}^T{\Sigma }_1\mathbf{w}}$$

目标函数
$$\begin{array}{rl}J(\mathbf{w})& =\frac{\Vert {\mathbf{w}}^T{\mu }_0-{\mathbf{w}}^T{\mu }_1{\Vert }_2^2}{{\mathbf{w}}^T{\Sigma }_0\mathbf{w}+{\mathbf{w}}^T{\Sigma }_1\mathbf{w}}\\ & =\frac{{\mathbf{w}}^T({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T{\mathbf{w}}^T}{{\mathbf{w}}^T({\Sigma }_0+{\Sigma }_1)\mathbf{w}}\end{array}$$

其中，$S_w$为类内散度矩阵（within-class scatter matrix）
$$S_w={\Sigma }_0+{\Sigma }_1$$

$S_b$为类间散度矩阵(between-class scaltter matrix)

$$S_b=({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T$$

目标函数重写为
$$J(\mathbf{w})=\frac{{\mathbf{w}}^T{S}_b\mathbf{w}}{{\mathbf{w}}^T{S}_w\mathbf{w}}$$
上式就是广义瑞利商。要取得最大值，只需对目标函数求导并等于0，可得到等式
$$S_b\mathbf{w}({\mathbf{w}}^T{S}_w\mathbf{w})=S_w\mathbf{w}({\mathbf{w}}^T{S}_b\mathbf{w})$$

重新代入目标函数可知
$$S_w^{-1}{S}_b\mathbf{w}=\lambda \mathbf{w}$$
这是一个特征值分解问题，我们目标函数的最大化就对应了矩阵 $S_w^{-1}{S}_b$ 的最大特征值，而投影方向就是这个特征值对应的特征向量。

多分类

可以将 LDA 推广到多分类任务中，目标变量 y i ∈ { c 1 , c 2 , ⋯   , c K } y_i\in \{c_1,c_2,\cdots,c_K\} yi​∈{c1​,c2​,⋯,cK​} 。

定义类内散度矩阵（within-class scatter matrix）
$$S_w=\sum _{k=1}^K{\Sigma }_k$$

类间散度矩阵(between-class scaltter matrix)

$$S_b=\sum _{k=1}^K{N}_k({\mu }_k-\mu )({\mu }_k-\mu {)}^T$$

其中 $\mu$ 为所有样本均值向量
$$\mu =\frac{1}{N}\sum _{i=1}^N\mathbf{x}$$
常见的最大化目标函数为
$$J(W)=\frac{\text{tr}(W^T{S}_{b}W)}{\text{tr}(W^T{S}_{w}W)}$$
对目标函数求导并等于0，可得到等式
$$\text{tr}(W^T{S}_{w}W)S_{b}W=\text{tr}(W^T{S}_{b}W)S_{w}W$$
重新代入目标函数可知
$$S_{b}W=\lambda S_{w}W$$
$W$ 的闭式解则是 $S_w^{-1}{S}_b$ 的 $K一1$ 个最大广义特征值所对应的特征向量组成的矩阵。

由于$W$是一个利用了样本的类别得到的投影矩阵，则多分类 LDA 将样本投影到 $K-1$ 维空间，$K-1$ 通常远小子数据原有的特征数。于是，可通过这个投影来减小样本点的维数，且投影过程中使用了类别信息，因此 LDA也常被视为一种经典的监督降维技术。

二次判别分析

下面来介绍以概率的角度来实现线性判别分析的方法。我们的目的就是求在输入为 $\mathbf{x}$ 的情况下分类为 $c_k$ 的概率最大的分类：
$$\hat{y}=\arg \underset{c_k}{\max }\mathbb{P}(y=c_k|\mathbf{x})$$
利用贝叶斯定理，类别 $c_k$ 的条件概率为
$$\mathbb{P}(y=c_k|\mathbf{x})=\frac{\mathbb{P}(\mathbf{x}|y=c_k)\mathbb{P}(y=c_k)}{\mathbb{P}(\mathbf{x})}$$

假设我们的每个类别服从高斯分布
$$\mathbb{P}(\mathbf{x}|y=c_k)=\frac{1}{\sqrt{(2\pi {)}^p\det {\Sigma }_k}}\exp \left(-\frac{1}{2}(\mathbf{x}-{\mu }_k{)}^T{\Sigma }_k^{-1}(\mathbf{x}-{\mu }_k)\right)$$

其中，协方差矩阵${\Sigma }_k$ 为对称阵。

决策边界：为方便计算，我们取对数条件概率进行比较。对任意两个类别$c_s$和$c_t$，取

$$\delta (\mathbf{x})=\ln \mathbb{P}(y=c_s|\mathbf{x})-\ln \mathbb{P}(y=c_t|\mathbf{x})$$

输出比较结果

$${\hat{y}}_{st}=\{\begin{array}{ll}{c}_s,& \text{if }\delta \le 0\\ c_t,& \text{otherwise}\end{array}$$

决策边界为 $\delta (\mathbf{x})=0$，即
$$\ln \mathbb{P}(y=c_s|\mathbf{x})=\ln \mathbb{P}(y=c_t|\mathbf{x})$$

我们先来化简下对数概率
$$\begin{array}{rl}\ln \mathbb{P}(y=c_k|\mathbf{x})& =\ln \mathbb{P}(\mathbf{x}|y=c_k)+\ln \mathbb{P}(y=c_k)-\ln \mathbb{P}(\mathbf{x})\\ & =-\frac{1}{2}(\mathbf{x}-{\mu }_k{)}^T{\Sigma }_k^{-1}(\mathbf{x}-{\mu }_k)-\frac{1}{2}\ln (\det {\Sigma }_k^{-1})+\ln \mathbb{P}(y=c_k)+\text{const}\\ & =-\frac{1}{2}{\mathbf{x}}^T{\Sigma }_k^{-1}\mathbf{x}+{\mu }_k^T{\Sigma }_k^{-1}\mathbf{x}-\frac{1}{2}{\mu }_k^T{\Sigma }_k^{-1}{\mu }_k+\ln \mathbb{P}(y=c_k)-\frac{1}{2}\ln (\det {\Sigma }_k^{-1})+\text{const}\\ & ={\mathbf{x}}^T{A}_k\mathbf{x}+{\mathbf{w}}_k^T\mathbf{x}+b_k+\text{const}\end{array}$$

其中
$$A_k=-\frac{1}{2}{\Sigma }_k^{-1},{\mathbf{w}}_k^T={\mu }_k^T{\Sigma }_k^{-1},b_k=-\frac{1}{2}{\mu }_k^T{\Sigma }_k^{-1}{\mu }_k+\ln \mathbb{P}(y=c_k)-\frac{1}{2}\ln (\det {\Sigma }_k^{-1})$$

可以看到，上式是一个关于 $\mathbf{x}$ 的二次函数

• 当类别的协方差矩阵不同时，生成的决策边界也是二次型的，称为二次判别分析(Quadratic Discriminant Analysis, QDA)
• 当类别的协方差矩阵相同时，决策边界将会消除二次项，变成关于 $\mathbf{x}$ 的线性函数，于是得到了线性判别分析。

实际应用中我们不知道高斯分布的参数，我们需要用我们的训练数据去估计它们。LDA使用估计协方差矩阵的加权平均值作为公共协方差矩阵，其中权重是类别中的样本量：
$$\hat{\Sigma }=\frac{{\sum }_{k=1}^K{N}_k{\Sigma }_k}{N}$$

如果 LDA中的协方差矩阵是单位阵 $\Sigma =I$并且先验概率相等，则LDA只需对比与类中心的欧几里得距离
$$\ln \mathbb{P}(y=c_k|\mathbf{x})\propto -\frac{1}{2}(\mathbf{x}-{\mu }_k{)}^T(\mathbf{x}-{\mu }_k)=-\frac{1}{2}\Vert \mathbf{x}-{\mu }_k{\Vert }_2^2$$

如果 LDA中的协方差矩阵非单位阵并且先验概率相等，则为马氏距离
$$\ln \mathbb{P}(y=c_k|\mathbf{x})\propto -\frac{1}{2}(\mathbf{x}-{\mu }_k{)}^T{\Sigma }_k^{-1}(\mathbf{x}-{\mu }_k)$$

---

1. 超平面几何知识 ↩︎